Etude Structurale et Dynamique de Solutions de Sucre Confinées

Chapitre 2

LA DIFFUSION NEUTRONIQUE APPLIQUEE A LA DYNAMIQUE MOLECULAIRE

2.1. Les neutrons et la diffusion neutronique 35

2.2. Dynamique moléculaire du sucre en solution aqueuse par QENS 41

2.2.1 Dynamique moléculaire du D-glucose

2.2.2 Dynamique moléculaire du D-fructose

2.3. Conclusion générale du chapitre 2 70

CHAPITRE 2

LA DIFFUSION NEUTRONIQUE APPLIQUEE A LA DYNAMIQUE MOLECULAIRE

2.1. LES NEUTRONS ET LA DIFFUSION NEUTRONIQUE

2.1.1. Le neutron et les interactions rayonnement-matière

Le neutron, découvert en 1932 par James Chadwick, est une particule subatomique qui présente une charge électrique nulle, une masse m = 1,675.10^-27 kg (~ 1836 fois celle de l'électron), un spin ¹/2 et un moment magnétique X = -1,9132 41n* ^.80,81,82,83 L'énergie d'un neutron E est reliée à sa vitesse v

par la relation E = ¹/2 m.v². A cette particule est associée une onde plane de vecteur d'onde k , de longueur d'onde 2 et d'énergie E :

Longueur d'onde :	h	Energie :	E	h^2 h^2.k^2
	m.v			2m2^2 2m

2 h.k

k

Vecteur d'onde : k = Moment : » = = h .

2

où h est la constante de Planck, et h = h / 2= 1, 055× 10^-34J.s est la constante de Dirac.

A cause de leur charge électrique nulle, les neutrons n'ont pas d'interactions électrostatiques avec le nuage électronique de l'atome à la différence d'autres particules comme les rayons X ou les électrons. En revanche, ils sont sensibles aux nucléons du noyau et c'est avec eux qu'ils interagissent par des forces « nucléaires » de courte portée (~ 10^-12 cm). Et comme les neutrons sont 100 000 fois plus petits que la distance noyau-noyau, leur probabilité d'interaction est de fait relativement faible, ce qui leur permet de pénétrer la matière en profondeur. (Figure 10) Les longueurs d'onde associées aux neutrons froids et thermiques sont de l'ordre de grandeur des distances interatomiques présentes dans les solides ou les liquides denses (1 < l < 800 Å), et leurs énergies sont comparables à celles des mouvements moléculaires (10^-13 < t < 10^-7 s). (Tableau 2) Les neutrons sont donc un outil de choix pour sonder la structure et la dynamique atomique de la matière condensée.

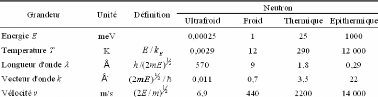
Tableau 2 : Caractéristiques des neutrons à différentes énergies sélectionnées.⁸⁰

* i_n est une constante physique appelée magnéton nucléaire 1 u_n= 5,050 783 43× 10^-27 A.m².

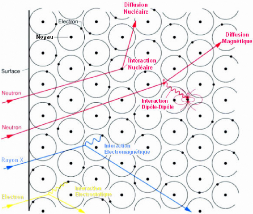
Figure 10: Interactions matière-rayonnem ent pour des neutrons, des rayons X et des électrons.

La force d'interaction nucléaire entre un neutron lent et un noyau est caractérisée par une grandeur appelée longueur de diffusion b. Cette grandeur définit la zone autour de l'atome dans laquelle le neutron va pouvoir interagir avec le noyau: il y a interaction lorsque le neutron pénètre dans la sphère de rayon b centrée sur l'atome. A la différence des rayons X, le signe^* et la valeur de b varient de manière irrégulière en fonction du numéro atomique Z et de la masse atomique A, ce qui rend les neutrons particulièrement sensibles à la présence d'atomes légers comme l'hydrogène par exemple.

Mais la situation est en réalité bien plus complexe car les interactions ne sont pas uniquement
d'origine nucléaire, mais également magnétique. Comme le neutron présente un spin 1/2, il est sensible
au spin nucléaire du noyau I. Dès lors que le noyau du centre diffusant possède un spin I, la longueur

de diffusion b peut prendre les valeurs b ou b correspondant aux états I + 1/2 ou I - 1/2 du système
respectivement. Dans la pratique, les neutrons sont diffusés au hasard soit avec une longueur b soit

avec une longueur b et il est donc nécessaire de définir une longueur de diffusion moyenne. Pour un
élément donné, constitué de différents isotopes a, d'abondance c_a et de spin nucléaire I_a, la longueur

de diffusion moyenne b vaut alors:

c

b I b I b

a ( 1)

a a a a

a a

2 1

I

Il est intéressant de constater que les longueurs de diffusion de deux isotopes sont généralement très différentes. (Cf. Tableau 3) Ainsi une simple substitution isotopique permet de moduler les

* Pour certains éléments ou isotopes, b peut prendre des valeurs négatives: b(Ti) = -3,370×10¹² cm, b(⁴⁶Ti) = 4,72×10¹² cm.

intensités de diffusion en augmentant l'intensité relative des zones d'intérêts et en diminuant celle des zones moins intéressantes. Il est alors possible de caractériser de manière très sélective les constituants d'un système sans en modifier de manière importante leurs propriétés physico-chimiques.