Etude Structurale et Dynamique de Solutions de Sucre Confinées

2.1.2. Principe de la diffusion neutronique

Une expérience de diffusion neutronique, comme celle schématisée sur la figure 11, consiste à

~ envoyer sur l'échantillon un faisceau de neutrons de vecteur d'onde ki

et d'énergie Ei . La majorité

des neutrons est transmise sans interaction, tandis qu'une infime partie est diffusée et mesurée par un
détecteur. A suffisamment grande distance du détecteur, l'onde diffusée peut être considérée comme

~ plane avec un vecteur d'onde kf

~ ~ tel que ki; kf

, et une énergie Ef . Lors du phénomène de

diffusion, le neutron et le système diffusant échangent simultanément un moment et une énergie. Les lois de conservation de l'énergie et du moment nous permettent d'exprimer littéralement ces transferts :

? ²

Pour le transfert d'énergie^* E = E -- E_f = h Am = h(co_i -- w) = ² - ²)

2m

~ ~ ~

Pour le transfert de moment^** Q = k _i-- k f

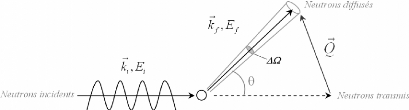
Figure 11 : Représentation schématique d'une expérience de diffusion.

Dès lors que l'on envoie un courant de particules sur une surface, il est possible de définir une section efficace a, dont l'unité est le barn^***. Durant une expérience de diffusion, l'état du neutron incident est susceptible d'être modifié en énergie, en direction et en spin. Trois types de sections efficaces peuvent alors être distinguées :

· La section efficace totale de diffusion aS qui prend en compte tous les neutrons diffusés.

· La section efficace différentielle de diffusion d/d qui comptabilise tous les neutrons diffusés dans l'angle solide d et quelle que soit leur variation d'énergie.

* Par convention, E est choisi positif lorsque le neutron cède de l'énergie au système.

~~ ** Le vecteur Q

caractérisant le transfert de moment est également dénommé vecteur de diffusion.

*** L'unité de section efficace est le barn (b) : 1b = 10^-28 m².

La section efficace double différentielle de diffusion d²/ddE qui comptabilise tous les neutrons diffusés dans l'angle solide d et avec une variation d'énergie dE.

2

Ces différentes sections efficaces sont liées par l'identité suivante:

S

d^adn ₌rr d 6 ddE dddE

De façon générale, le spectre d'énergie de l'intensité diffusée par unité d'angle solide n et pour un transfert en énergie E #177; dE s'écrit :

~~

d²a(Q,E)

I_f(Q,E)-- I0 dû.dE

où I0 est l'intensité incidente et I_f(Q,E) est une quantité qui reflète à la fois la structure et la dynamique d'un système.

2.1.3. Diffusion cohérente et incohérente

La section efficace double différentielle de diffusion d'un système peut être décomposée en deux termes qui représentent la diffusion cohérente et la diffusion incohérente :

d²o- k ₀-

dn2E k^f_i 4 Scoh k (Q,E)₊ f ainc S (Q E)

^cir^oh

i

où

~~ coh , ^Cr inc , Scoh(Q, )

~~* et S inc(Q, E)

sont les sections efficaces et les fonctions de diffusion ou

facteur de structure dynamique cohérent et incohérent respectivement.

La diffusion cohérente (1^er terme) dépend de la corrélation entre la position de l'atome i au temps 0 et celle de l'atome i' au temps t. Ce terme contient tous les termes d'interférence. La diffusion incohérente (2^nd terme) dépend de la corrélation entre la position de l'atome i au temps 0 et celle du même atome au temps t. Autrement dit, la partie cohérente représente l'interaction entre paires d'atomes différents, et la partie incohérente représente l'interaction de chaque atome avec lui-même.

* Les expressions de _Scoh(Q,E) et Si_nc(Q,E) sont données ici à titre indicatif:

1 ~~\\ \\

Scoh(Q, E) 2n?

= exp(--iot)E expLQR! 0)) exp iQ
· Rjt)) dt

N jj

\ 1 r 1 \\ ~~~ ~~

(t)) S_inc (Q, E) = expHCOOE exp^/--QR j 0))exp^/iQ. Rj ^It)) dt

2?N j

Les fonctions de diffusion sont les transformées de Fourier en énergie des fonctions intermédiaires de diffusion cohérente I_coh(Q,t) et incohérente Ii_nc(Q,t).

Dans le cas d'un système polyatomique, la double différentielle de diffusion prend alors l'expression suivante:

d

² k

c c b b S Q E

1/ 2 1/ 2 * '

dd k f

^f ( , ) ( , )

c S Q E

d

d d d d coh

' ' d inc

d dE k i d

k

dd ' i

où c_dN_d N est la concentration de l'élément d.

Les sections efficaces cohérente et incohérente, dont leurs expressions littérales sont données ci- dessous, sont fonction de la longueur de diffusion b qui est propre à chaque atome:

2

4 b 2 *

b

inc [ ?

2

coh 4 b

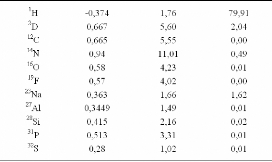
La section efficace totale de diffusion est la somme des sections efficaces cohérente et incohérente_inc . Le tableau 3 présente les sections efficaces cohérente et incohérente

total coh

de quelques éléments communs de la classification périodique. Au vue de la section efficace incohérente de l'hydrogène, qui est très largement supérieure à celle des autres noyaux mais également à sa propre section efficace cohérente, la diffusion des neutrons sera donc par nature essentiellement incohérente à petits Q pour des systèmes hydrogénés.

Tableau 3: Longueurs de diffusion b et les sections efficaces cohérente et incohérente pour quelques éléments du tableau périodique.⁸⁴

* b est la longueur de diffusion moyenne pour un élément donné. (Cf. le paragraphe précédent).

2

b best la déviation quadratique moyenne, où

c_a 2 2

b I b I b

2 ( 1)

a a a a

a I_a

2 1

2

. Physiquement,

la diffusion incohérente provient de la distribution aléatoire des écarts à la moyenne des longueurs de diffusion.

Le tableau 3 montre clairement que deux isotopes peuvent présenter des valeurs de a_coh et a_inc très

différentes. Ainsi, par exemple, on remarquera le grand écart existant entre les sections efficaces incohérentes de l'hydrogène (¹H) et du deutérium (²H). Cette propriété, très marquée dans le cas de l'hydrogène, se retrouve chez d'autres atomes, comme l'ytterbium ou le gadolinium, ou chez certains isotopes comme le titane. Le mélange des isotopes nous permettra donc de jouer sur les densités de longueurs de diffusion, ce qui nous permettra de caractériser les mouvements individuels des atomes d'hydrogène dans le cadre d'études de dynamique moléculaire.