3.4. ETUDE STRUCTURALE PRELIMINAIRE DES GELS DE SILICE
AQUEUX CONTENANT DU D-GLUCOSE PAR DIFFUSION DES NEUTRONS AUX PETITS ANGLES
La diffusion des neutrons aux petits angles (SANS) est une
technique non-destructrice, qui, en mesurant la diffusion pour les faibles
valeurs de transfert de Q, permet d'étudier la géométrie
et la morphologie d'inhomogénéités de taille relativement
importante, généralement comprises entre 5 et 500 nm,
c-à-d pour 10-3 < Q < 0,5 Å-1. (Figure
31) Grâce à la gamme de tailles explorée et aux
particularités liées à la nature même des neutrons,
le SANS se révèle être un outil de choix pour sonder la
microstructure des matériaux et se voit être un très bon
complément des microscopies électroniques (MEB, MET) et optique,
mais également de la diffraction.
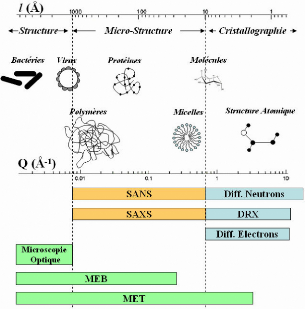
Figure 31 : Exemples de quelques objets dont les tailles sont
comprises entre 1 nm et 1 ,um. En dessous sont
présentées quelques techniques qui devraient
être utilisées dans cette gamme de taille.
3.4.1. Le formalisme de la diffusion aux petits angles
Dans le cas de la diffraction de Bragg classique, une intense
diffusion élastique cohérente est observée à chaque
fois que la loi de Bragg est satisfaite, c-à-d lorsque 2 = 2d
sinè 2, où d est une
0
distance caractéristique du réseau. Dans le cas
d'inhomogénéités « périodiques »,
séparées d'une
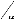
distance d, la diffusion se produit alors seulement aux angles de
Bragg où Q= 2ff 80,116
'
d

Il est alors possible de définir le vecteur d'onde
à la résonance de Bragg Q:
Q=4 sin sin
2
Durant une expérience de diffusion, l'intensité
diffusée I(Q) est mesurée en fonction de l'angle de diffusion, et
s'exprime sous la forme suivante :
I(Q) = 00.M.2.77.T.d.
d
d
où
= 0 est le flux de neutrons incidents, OSZ est l'angle solide
considéré,
est l'efficacité du détecteur,
T est la transmission de l'échantillon, d est
l'épaisseur de l'échantillon,
d est la section efficace différentielle de diffusion.
d
L'objectif de la mesure est donc de déterminer la
section efficace différentielle de diffusion, qui contient toute
l'information sur la forme, la taille et les interactions régnant dans
le système entre les entités diffusantes.
Dans des milieux isotropes contenant des particules relativement
lourdes comparée à la masse
du neutron, les diffusions élastique et
quasi-élastique, pour lesquelles

prédominent.117,118, 119 Dans ces
conditions, l'approximation statique peut-être utilisée pour
exprimer la section différentielle de diffusion par unité de
volume du matériau dE dQ . Pour un échantillon
composé de N atomes l, de longueur de diffusion bl, nous avons :

2
dE
bl
eie
N
1
V
L'angle de diffusion est habituellement appelé
20.
En général, la longueur de diffusion bl
dépend de la nature du noyau et de son état de spin. Il est alors
plus commode de séparer la section différentielle de diffusion
par unité de volume cohérente de celle incohérente :
dE dE lcoh dE linc
d l d J l d
où
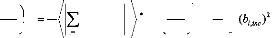
2
coh
N
1
dE
E
eiQRl
**
bl,coh
l
1
d
et = E
V
inc1N
d V
La diffusion cohérente a une distribution spatiale
caractéristique de la distribution des atomes dans l'échantillon
et donne des informations sur la structure d'un composé. Il est alors
possible de déterminer la structure et la taille d'un objet à
basse résolution. La diffusion incohérente, quant à elle,
ne donne qu'un bruit de fond indépendant de Q qui est proportionnel
à la section efficace de diffusion incohérente inc.
Il est alors possible de réécrire la section
efficace sous une forme plus simple :
d dE (A4)2 C pVpP(Q)S(Q)+
Binc
dans laquelle Cp est la fraction volumique des
diffuseurs, Vp le volume d'un diffuseur, (4)2 le
facteur de contraste, P(Q) le facteur de forme, S(Q) le facteur de structure et
Binc le bruit de fond incohérent. Nous reviendrons en
détail sur ces notions dans le chapitre 4.
| 


