3.4.2. Interprétation qualitative des
différents domaines de Q
Comme nous avons pu le voir, Q et d sont inversement
proportionnels, en d'autres termes, lorsque Q croît, d diminue et vice
versa. Ainsi, plus on augmente la valeur de Q, plus les détails de
petite taille sont mis à jour. D'une manière plus imagée,
jouer avec la valeur de Q, revient à jouer avec le grossissement d'un
microscope. La figure 32 schématise cette idée et présente
les différents domaines suivant les valeurs de Q
considérées.
* Nous rappelons que : bl,coh bl ** et que : bl2inc
bl2 -- b l 2
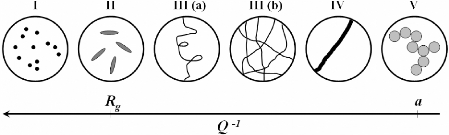
Figure 32 : Représentation schématique des
différents domaines de Q dans le cas d'une solution
diluée.118
Pour des valeurs de Q proche de 0 (Cas I), chaque
molécule est vue pratiquement comme un point, et il est impossible
d'obtenir une quelconque information sur sa structure. Maintenant, augmentons
la valeur de Q pour avoir Qf1 de l'ordre du rayon de giration
Rg (II). Si l'observation de la forme des molécules n'est
maintenant plus possible, leur forme générale apparaît et
c'est dans ce domaine, appelé domaine de Guinier, que l'on
mesurera leur rayon de giration Rg. Si l'on augmente encore un peu
plus la valeur de Q, nous atteignons les domaines III(a) et III(b). Pour une
solution diluée (Cas III(a)), seule une partie de la chaîne est
visible et il est alors possible de déterminer sa longueur de
persistance. Dans le cas d'une solution semi-diluée cette fois (Cas
III(b)), ce n'est pas un, mais plusieurs bouts appartenant à des
chaînes différentes que l'on observe. Il existe alors de nombreux
points de contacts entre les différentes chaînes, et la longueur
d'une chaîne entre deux ramifications devient une distance
caractéristique de l'échantillon appelée longueur de
corrélationî. En augmentant encore un peu plus la valeur de Q (Cas
IV), le polymère apparaît comme une chaîne gaussienne si la
longueur de persistance est plus petite que Q1, ou comme un
bâton si la longueur de persistance est plus grande que Q1.
Ces domaines III et IV vont constituer ce que l'on appelle le régime
de Porod. Enfin, pour des valeurs de Q, telles que
Qf1 soit de l'ordre de grandeur des liaisons chimiques (Cas
V), la structure locale de la chaîne pourra alors
être déduite. Au-delà, c-à-d pour des valeurs
correspondant aux grands angles, il est possible d'obtenir des informations sur
les distances interatomiques par des méthodes telles que l'analyse de
Rietveld. Cette région est désignée comme le domaine de
Bragg.
La figure 33 représente schématiquement une
courbe de diffusion aux petits angles dans le cas d'une solution diluée
de macromolécules. Le tracé log-log de l'intensité de
diffusion en fonction de Q a été découpé en suivant
les domaines de Guinier, de Porod et de Bragg définis
précédemment.
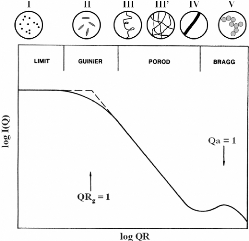
Figure 33 : Représentation schématique d'une
courbe de diffusion aux petits angles pour une solution
diluée de macromolécules (Rg
est le rayon de giration du polymère considéré, et a est
une longueur de liaison
interatomique).101
Revenons un peu plus en détail sur les régimes de
Guinier et de Porod :
Dans le régime de Guinier, correspondant à des
petits angles de diffusion (QRg rs, 1),
l'intensité diffusée est reliée au rayon de giration
Rg par l'expression suivante :
I(Q) ~ eQ2Rg2 3 .
Le tracé du logarithme de la section efficace en fonction
de Q2 doit donc donner une droite, dont la pente pour Q -->
0 permet de déterminer Rg . Ce tracé est
appelé représentation de Guinier.
Enfin, le régime de Porod, qui correspond à des
valeurs d'angles de diffusion intermédiaires (Rg »
Q-1 » a), présente une décroissance de
l'intensité diffusée qui suit une loi de puissance :
I (Q) ~ Q- X
avec -X = -2df+ dS= P dans laquelle P est la pente de Porod, df
la dimension du fractal de masse (0 = df= 3) et dS la dimension du fractal de
surface (2 = df= 3).
Dans le cas d'objets uniformes mais non-fractal, df = 3, dS =
2, et P vaut donc - 4. Dans le cas d'objets présentant un fractal de
masse, alors df = dS et donc P = - df. Dans ce cas, la dimension fractale est
obtenue directement en mesurant la pente. Dans le cas d'un fractal de surface,
df= 3 et P = dS - 6.

Le tableau 22 présente quelques valeurs de la pente de
Porod pour différents types de structure polymériques. Il
apparaît donc qu'à partir de l'analyse de la pente de Porod, on
peut en déduire une quantité importante d'information concernant
les dimensions fractales.
Tableau 22 : Quelques exemples de pentes de Porod pour
différentes structures.101
| 


