3.4.3. Paramètres expérimentaux
Les gels ont été synthétisés
directement dans des cellules en titane démontables mises à notre
disposition. Les échantillons, de 2 mm d'épaisseur, sont pris en
sandwich entre deux fenêtres en quartz, des joints et serre-joints
réalisant l'étanchéité. Les mesures ont
été réalisées sur l'instrument de diffusion aux
petits angles NG-3 30m120 en collaboration avec Dr S. Kline du
National Center for Neutron Research (NCNR). Une longueur d'onde incidente de 6
Å et trois distances détecteur- échantillon de 1,3, 4 et 13
m ont été utilisées alternativement pour permettre de
couvrir une grande gamme de Q (0,0035-0,47 Å-1).
3.4.4. Résultats et discussion
Les spectres ont été corrigés de la
cellule vide et de l'efficacité des détecteurs, puis
normalisés et enfin moyennés sur tous les angles pour chaque
position du détecteur. Les trois parties ont ensuite été
mises bout à bout pour recréer le spectre complet qui
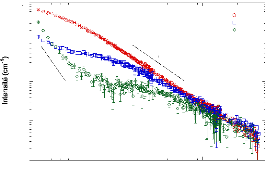
s'étale sur toute la gamme de Q considérée. La figure 34
présente les spectres corrigés des gels A1, A2 et A3. Les
intensités de diffusion en fonction de Q présentent des
changements importants en fonction de la concentration en D-glucose et plus
particulièrement pour les plus faibles valeurs de Q. Dès lors que
l'on ajoute du sucre, le spectre présente une remontée en
intensité à petits Q, qui s'intensifie avec la concentration.
Dans le cas de A3, le plus concentré, cette remontée
présente même une pente en Q-4, qui indique la
présence d'une interface marquée, et donc
d'inhomogénéités plus larges.
10
Al
A2
A3
1
Q-2
Q-4
0,1
0,01
0,001
0,01 0,1
Q(Å-1)
Figure 34 : Spectres SANS des gels A1 (rouge), A2 (bleu) et A3
(vert).
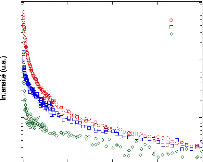
Ces spectres, dans la représentation de Guinier,
montrent de manière non équivoque qu'il n'existe pas de longueur
d'échelles caractéristiques dans ces échantillons. La
seule grandeur possiblement accessible est le rayon de Guinier R0 correspondant
à de petites particules formant la structure de base du gel. Ce rayon se
détermine à partir de la pente pour Q ? 0 du profil de diffusion.
(Figure 35)
10
Al
A2
A3
1
0,1
0 0,002 0,004 0,006 0,008
Q2 (Å2)
Figure 35: Représentation de Guinier pour les trois gels
A1, A2 etA3.
Une estimation rapide de la pente de Porod donne une valeur
assez proche de 2. Afin de définir avec précision la dimension
fractale de nos gels et le rayon de Guinier, nous avons ajusté ces
spectres de diffusion à l'aide d'un modèle
fractal121,122 souvent utilisé dans le cas des gels de silice
de la forme:
I Q
( )( ) ( ) te
P Q S Q C
où P(Q) est le facteur de forme des particules
monomériques sphériques formant la structure fractale
Cte
et la est le bruit de fond incohérent indépendant
de Q. Le facteur de structure fractal S(Q) est
121,122
donné par :
sin ( 1) tan ( ) ( 1)
1
[ D Q D D
î ]
S Q
( ) 1 (Eq. 22)
( ) D 1 1 D
( 1) 2
QR Q 2 2
0 [ ]
î
dans laquelle D est la dimension fractale, R0 le rayon des
particules de silice formant la structure primaire, et î la
longueur de corrélation interprétée ici comme le
diamètre moyen des pores présents dans le gel de silice.
Les spectres des trois gels ont été
ajustés afin d'extraire les informations sur le gel (Figure 36). Ce
modèle ajuste parfaitement les données du gel A1. En ce qui
concerne les gels A2 et A3, l'accord est bon sur la majeure partie des spectres
excepté à petits Q où une déviation apparaît
et s'intensifie avec la concentration. Cette déviation peut être
due : (i) à la présence de large
inhomogénéités dans l'échantillon, ou (ii) à
des zones «riches en sucre », qui pourraient correspondre à
une séparation de phase par exemple, ou (iii) à une autre origine
qu'il reste à déterminer.
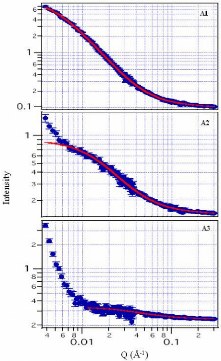
Figure 36: Spectres SANS pour les échantillons A1, A2 et
A3. Les courbes rouges représentent les ajustements du modèle
fractal décrit précédemment dans le texte.
Ainsi, nous avons déterminé que la dimension
fractale est D = 1,9 #177; 0,1. Cette valeur est tout à fait typique
d'un gel polymérique ramifié présentant un fractal de
masse (Tableau 22). De plus, le diamètre de Guinier, c-à-d la
taille des particules primaires, a été trouvée
égale à R0 = 6 #177; 1 Å. Notons que D et R0
présentent des valeurs quasi-identiques pour les trois gels. En revanche
la longueur de corrélation î diminue avec la
concentration, passant de 188 #177; 4 Å pour A1, à 70 #177; 3
Å et 25 #177; 7 Å pour les gels A2 et A3 respectivement.
Parmi tous les travaux existants sur le sujet, l'étude
de Schaefer et al.123 portant sur l'évolution du profil de
diffusion SAXS d'un sol en fonction du temps de gélation nous
apparaît très adéquate pour interpréter nos
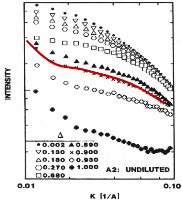
résultats. La figure 37 présente le régime de Porod d'un
sol en fonction du temps normalisé par rapport à la
gélation. Il est clair que le spectre de diffusion dépend
fortement du temps de gélification. Ainsi le sol présentera un
profil très irrégulier, alors qu'à la fin de la
gélification, le régime de Porod est atteint et permet de mesurer
la dimension fractale du gel final.
GEL
SOL
,123
Figure 37 : Evolution du profil de diffusion SAXS en fonction du
temps de gélation.101La courbe en rouge n'est qu'une aide
visuelle.
Les spectres intermédiaires entre le sol et le gel
laissent apparaître des profils présentant une remontée
à petits Q très similaire à celle observée pour nos
gels A2 et A3 contenant du sucre. L'origine de cette remontée serait
donc à rapprocher d'une gélification incomplète. Afin de
répondre à cette question, le gel contenant 30% de glucose a
été placé quelques heures supplémentaires en
vieillissement, avant d'être mesuré de nouveau. (Figure 38) Le
spectre ainsi obtenu a fortement évolué et présente
maintenant un profil typique d'un gel dans le régime de Porod. Cette
hypothèse est de plus corroborée par les valeurs
décroissantes de la longueur de corrélation î lorsque la
concentration en sucre augmente. Il est également intéressant de
constater, que pour une même durée de vieillissement, les gels A1,
A2 et A3, présentent des temps de gélifications
différents. Il y a donc un effet de la
concentration en sucre sur la cinétique de
gélification, qui se traduit par une diminution de la cinétique
de polymérisation avec l'ajout de sucre.
100
10
1
0,1
0,01
0,001
0,0001
0,01 0,1
Q (Å1)
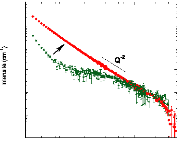
Figure 38 : Evolution du profil de diffusion du gel contenant 30%
de glucose avec le temps de gélification. La courbe verte a
été mesurée après 15h de vieillissement, la courbe
rouge après 20h.
Nous avons donc estimé le diamètre moyen des
pores à 18,8 nm. Il est de plus important de noter que ces trois gels
ont été préparés spécialement pour les
mesures de diffusion quasi-élastique des neutrons, et qu'ils
n'étaient donc pas optimisés pour observer la structure du
réseau de silice par SANS. En effet, l'ajout du sucre dans le gel va
modifier le contraste de la solution. Cette première série de
mesure nous permet donc d'apprécier l'importance du temps de
gélification sur le profil de diffusion mesuré, mais elle
nécessite néanmoins une étude complémentaire afin
d'asseoir de manière définitive cette interprétation d'une
gélification incomplète. C'est pour cette raison qu'une nouvelle
série de mesures SANS utilisant la technique de variation de contraste a
été réalisée sur ces gels. (Chapitre 4)
| 


