Etude Structurale et Dynamique de Solutions de Sucre Confinées

Chapitre 5

DYNAMIQUE MOLECULAIRE DU SUCRE CONFINE DANS UN GEL DE SILICE AQUEUX

5.1. Dynamique du D-glucose confiné dans des gels de silice 115

5.2. Dynamique du tréhalose confiné dans des gels de silice 122

5.3. Conclusion générale du chapitre 5 128

CHAPITRE 5

DYNAMIQUE MOLECULAIRE DU SUCRE CONFINE DANS UN GEL DE SILICE AQUEUX

D'après le chapitre précédent, il émerge que les sucres présentent une forte aptitude à conserver les édifices dans leur intégrité structurale. Cette conclusion confirme donc les hypothèses avancées pour expliquer la résistance des organismes anhydrobiotiques. Si cette étude structurale nous apporte une confirmation supplémentaire du rôle crucial des sucres, il reste néanmoins qu'elle ne fournit pas à elle seule quelles en peuvent être les causes ? Parmi les hypothèses évoquées pour de si grandes pertes en eau, la substitution de l'eau d'hydratation et la vitrification sont les deux phénomènes les plus probables. (Cf. Chapitre 1) Or ces deux hypothèses sont basées sur des questions d'interaction eau- soluté principalement. Ainsi, pour comprendre les origines mêmes de cette protection, il est absolument nécessaire d'étudier les aspects dynamiques des molécules de sucre, qui peuvent donner un aperçu des interactions au sein de ces solutions. Dans ce chapitre, nous allons donc étudier la dynamique des molécules de D-glucose d'une part, puis celle des molécules d' tréhalose d'autre part, confinées dans ces mêmes gels de silice. Nous pourrons donc regarder les effets de la taille de l'environnement sur leurs dynamiques respectives.

5.1. DYNAMIQUE DU D-GLUCOSE DANS LES GELS DE SILIC

5.1.1. Conditions expérimentales

Les mesures de dynamique moléculaire du D-glucose confiné, par diffusion quasi-élastique des neutrons, ont été réalisées au National Center for Neutron Research (NCNR) sur les spectromètres DCS⁸⁵ et HFBS.⁸⁶ La gélification des sols s'est faite directement dans des porte-échantillons cylindriques d'espace annulaire 0,4 mm. Une fois scellés, ils ont été placés dans un cryostat dans lequel la température est régulée à #177; 1 K.

Les trois échantillons A1, A2 et A3 ont été mesurés sur le DCS à 300 K, avec une longueur d'onde incidente de 6 Å (0,25 < Q < 1,93 Å^-1), et pour une résolution instrumentale de 57p,eV. Pour les mesures effectuées sur le HFBS, les paramètres expérimentaux étaient les suivants : T = 300 K, 2%, = 6,27 Å, 0,36 < Q < 1,52 Å^-1 avec une résolution de #177; 1,2 geV.

5.1.2. Traitement des données

Les spectres de chaque échantillon ont été normalisés au moniteur, corrigés de la cellule vide, normalisés au vanadium, puis regroupés afin d'améliorer la statistique. Cette partie du traitement est en tout point identique à celle décrite précédemment (Cf. Chapitre 2 : p. 40).

Afin d'extraire la dynamique des molécules de D-glucose, nous avons soustrait le gel sans sucre A1 des gels contenant du sucre (A2 et A3), les spectres résultants s'appelleront respectivement A2-A1 et A3-A1. Afin de prendre en compte les différents facteurs d'atténuation du gel pur (A1) et des gels contenant du sucre (A2 et A3), la diffusion de A1 a été multipliée par le facteur d'atténuation du D- glucose avant la soustraction. Le coefficient d'atténuation d'une espèce se calcule à partir du nombre d'atomes i par unité de volume ñi, de la section efficace de diffusion totale ⁱ, de la section efficace

S

i

d'absorption, et enfin du chemin optique x :

A

i i

A exp ( )

ñ x

espèce i S A

i?espèce

Si l'on suppose que la densité partielle du gel n'est pas affectée par la présence du sucre, alors le
coefficient d'atténuation d'un gel contenant du sucre est le produit des coefficients d'atténuations du

gel et du sucre : A gel A gel × A _glucose .

glucose

A titre d'exemple, la soustraction pour le gel A2 s'est effectuée de la manière suivante:

A2 - A1A2AgelglucoseCVA × glucoseA1 × AgelCV

où Agel+glucose est le coefficient d'atténuation du gel A2, Aglucose celui du D-glucose, et CV le signal de la cellule vide.

La validité de la procédure repose bien évidemment sur l'hypothèse que la présence du sucre n'affecte pas la dynamique du gel hôte. Cette hypothèse est supportée par le fait que le gel est deutéré et qu'il contribue donc relativement peu à la diffusion totale. (Tableau 25)

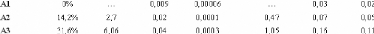
Tableau 25: Contributions relatives de la diffusion cohérente et incohérente émanant du D-glucose, de l'eau lourde et du gel.

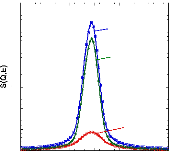
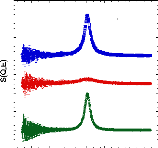
Les fonctions de diffusion des échantillons A1 et A3, et de la soustraction A3-A1, sont présentées sur la figure 51(a) pour le DCS pour Q = 0,7Å^-1 et sur la figure 51(b) pour le HFBS pour Q = 0,36Å^-1. Celles-ci montrent de manière claire que la contribution solvant/matrice est faible en comparaison de celle du D-glucose.

35

30

(a)

Q = 0.74⁴

T = 300 K

A3

25

A3-Al

20

1 5

10

5

0

Al

-0.3 -0.2 -0.1 0 0.1 0.2 0.3

E (meV)

-40 -30 -20 -10 0 10 20 30 40

(³)

T = 300 K Q = 0,364⁴

A3-Al

A3

Al

E (peV)

Figure 51: Fonctions de diffusion pour les échantillons A1 (rouge), A3 (bleu) et A3-A1 (vert) tirées des mesures réalisées sur le DCS (a) et sur le HFBS (b) à 300 K.