6.2.2.4. Diffusion des neutrons aux petits angles
La diffusion des neutrons aux petits angles a également
été utilisée afin de déterminer la microstructure
interne, ainsi que la morphologie des particules.187,188,189 Les
expériences ont été menées sur les
spectromètres NG-3 et NG-7129 au NIST Center for Neutron
Research à une longueur
d'onde incidente de 6 Å. Afin de couvrir une grande
gamme de Q comprise entre 0,0035 et 0,47 Å-1, trois distances
échantillon-détecteur de 1,3, 4 et 13 m ont été
utilisées séquentiellement. Cette technique présente le
grand avantage d'être non-destructrice, mais surtout de sonder une
très importante quantité de matière, donnant ainsi une
vraie image de l'échantillon dans sa globalité. La fonction de
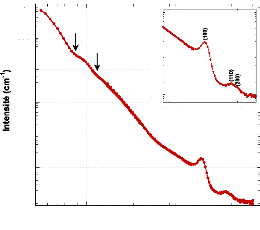
diffusion de l'échantillon MCM-0,1% est présentée dans la
figure 68.
1 04
1
1000
0.1
100
0.01
10
0.06 0.08 0.1 0.3
1
0.1
0.01
0.01 0.1
Q(A~1)
Figure 68: Spectre SANS de l'échantillon MCM-0,1 %.
L'encart représente un agrandissement de la zone des pics de Bragg
à grands Q correspondant à un arrangement hexagonal des pores.
Une étude minutieuse du spectre montre des
détails qui corroborent nos clichés MET et nos mesures de DRX.
Dans la région des petites valeurs de Q, c-à-d jusqu'à
0,08 Å-1, la fonction de diffusion présente deux minima
indiqués par des flèches à Q = 0,0075 Å-1
et à Q = 0,0 12 Å-1. La présence même de
ces oscillations, qui est liée à la présence d'objets
sphériques, témoigne de la faible dispersion en taille de nos
particules. Dans la région des relativement grandes valeurs de Q, trois
pics sont clairement visibles à Q = 0,15, 0,26 et 0,3
Å-1. A titre de comparaison, les pics de Bragg, obtenus en
DRX, apparaissaient pour des angles de 2,17°, 3,77° et 4,35°, ce
qui correspond à des valeurs de Q de 0,154, 0,268 et 0,309
Å-1 respectivement. Ces pics sont donc attribuables aux plans
(100), (110) et (200) d'un arrangement hexagonal des pores.190,191
Le SANS, qui présente une résolution plus limitée que les
rayons X pour ce type d'échantillon, ne permet pas de définir
avec précision les positions des pics de Bragg, et il est alors
difficile de conclure sur le déplacement du pic (100) avec la
concentration. Signalons, que la fonction de diffusion de l'échantillon
MCM-0,5%, qui n'est pas montrée ici, présente également
trois pics de Bragg, mais les oscillations à petits Q n'apparaissent pas
ou que très faiblement, prouvant ainsi la moins bonne dispersion en
taille de l'échantillon.
A la vue des différentes formes (billes, cylindres), du
nombre de longueurs de corrélation différentes mises en jeu, et
de l'organisation tridimensionnelle des pores (Figure 69), un ajustement global
de la fonction de diffusion sur une grande gamme de Q est assez
compliqué à réaliser. Néanmoins en superposant les
facteurs de forme des différents objets formant la structure, il est
possible d'en déduire de nombreuses informations structurales.

Figure 69: Cliché MET des nanosphères (MCM-0,1%).
Ces deux sphères montrent la longueur des pores cylindriques (~ 120 nm)
et leur arrangement hexagonal.
Les facteurs de forme ont été calculés de la
manière la plus simple qu'il soit, c'est-à-dire dans le cas de
sphères et de cylindres «idéaux », homodisperses en
taille et non-interagissant.
- Le facteur de forme d'une sphère de rayon r est
donné par l'équation suivante118,192:
2
sin( ) cos( )
Qr Qr Qr
P Q v
( ) 9( ) 2 2
ñ C te
sphères sphère ( ) 3
Qr

2
- Le facteur de forme des cylindres de rayon r et de longueur 2H
est donné par la relation192:
2
te
1 ( sin )
J Qr
( ) 2( ) ( cos ) sin
1
P Q v j QH
ñ d C
cylindres cyl 0
v ( sin )
Qr
cyl 0
dans lesquelles vsphere et vcyl sont les volumes
des particules sphériques et cylindriques,
(ñ)2 le contraste, J1(x) la fonction de Bessel au
premier ordre,l'angle entre l'axe du cylindre et le vecteur de diffusion
Q*, et Cte le background incohérent.
Les clichés MET nous permettent donc de calculer
effectivement ces facteurs pour des sphères d'un
rayon de 60nm, et
pour des cylindres d'un rayon de 1,7 nm et de longueur 120 nm. Les pics de
Bragg
ont été simulés grâce à des
fonctions gaussiennes G(Q,) centrées sur 0,15 Å-1, 0,26
Å-1 et 0,3 Å-1, et
* L'intégrale surmoyenne ainsi le facteur de forme sur
toutes les orientations du cylindre.
ce d'après les mesures de DRX. La fonction de diffusion
de l'échantillon MCM-0,1%, les facteurs de forme des cylindres et des
sphères, ainsi que les trois pics de Bragg correspondant à la
structure tridimensionnelle des pores sont présentés sur la
figure 70(a).
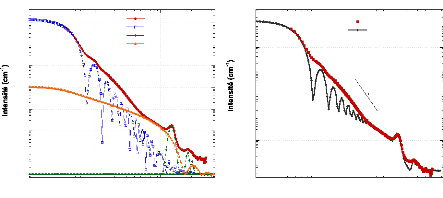
(a)
(b)
0.001
0.001 0.01 0.1
CI (A-1)
0.001 0.01 0.1
CI (A-1)
MCM-0,1%
FF Sphères
FS (Pics de Bragg) FF Cylindres
1000
104
Ajustement (Total)
MCM-0,1%
100
100
10
10
CI-4
1
1
0.1
0.1
0.01
0.01
104
1000
Figure 70 : Ajustement des différents facteurs de forme
des sphères, des cylindres et des pics de Bragg au spectre
expérimental (a). La figure (b) présente l'intensité
totale de toutes ces contributions comparée à celle de
l'échantillon MCM-0,1%.
Facteur de forme des sphères
Il apparaît très clairement que la
première partie du spectre (Q < 0,03 Å1) concerne
principalement les plus gros objets, en l'occurrence les sphères dans
leur globalité. Nous remarquons que les deux premiers minima
coïncident avec les oscillations visibles du spectre expérimental.
Le fait que ces oscillations ne soient pas plus marquées provient du
fait que les particules, bien que très régulières, ne
présentent pas une dispersion en taille idéale. Ainsi, la
dispersion en taille va se traduire par un lissage du spectre.
Néanmoins, cette valeur du diamètre (120 nm) est bien plus
représentative de l'échantillon que les images MET puisqu'elle
constitue une moyenne sur plusieurs centaines de milliards de particules,
prouvant ainsi la validité et la grande qualité de la
synthèse.
Facteur de forme des cylindres
Le facteur de forme des cylindres semble influencer le spectre
dans la région des moyennes et grandes valeurs de Q (0,03 < Q <
0,3 Å1). Il faut noter que l'utilisation de cylindres
identiques n'est pas tout à fait exacte. En fait, les cylindres ont des
longueurs variables pour pouvoir former un objet sphérique.
Néanmoins, l'approximation d'une longueur de cylindre fixe n'est
cependant pas si fausse à la vue du peu d'influence que peut avoir la
longueur L sur le facteur de forme P(Q).
Pics de Bragg
Les pics de Bragg, déterminés par rayons X,
coïncident parfaitement avec ceux présents sur le spectre SANS. Les
deux techniques nous donnent donc des résultats en bonne
adéquation.
Résultante
L'intensité résultante I(Q) est le produit du
facteur de forme P(Q) par le facteur de structure S(Q) :
I(Q) = P(Q)S(Q)
Or, les différentes formes en présence dans
l'échantillon, c-à-d des sphères et des cylindres, se
situent dans des échelles de longueur assez différentes. Le
facteur de forme des cylindres n'intervient vraiment que dans le Porod du
facteur de forme des sphères. Ce décalage nous permet alors
d'approximer le produit des facteurs de forme à une addition.
L'équation totale de I(Q), tenant compte de cette approximation, prend
alors la forme suivante :
I(Q) LPSphères(Q)#177; PCylindres(Q)1[1+
G(Q1,1) G(Q2, 2) +
G(Q3,3)]
dans laquelle le premier terme correspond au facteurs de forme,
et le deuxième au facteur de structure, qui correspond ici aux pics de
Bragg provenant de l'organisation hexagonale.
L'intensité résultante I(Q) est
présentée et comparée au spectre expérimental dans
la figure 70(b). L'ajustement réalisé par I(Q) est plutôt
correct sur toute la gamme de Q considérée. Pour 0,1 < Q <
0,3 Å-1, l'intensité simulée est plus faible,
indiquant que l'on sous-estime légèrement la surface des
sphères. Cette différence peut s'expliquer par le fait que notre
facteur de forme des sphères ne prend pas en compte une
légère polydispersité en taille. Par conséquent,
une petite variation du diamètre des sphères va alors avoir une
influence non-négligeable sur la surface totale.
Cette tentative d'ajustement, bien que sommaire, permet de
valider les grandeurs caractéristiques que nous avons
déterminées par microscopie et par diffraction. Un ajustement
global permettrait notamment de conclure avec beaucoup plus de précision
sur les valeurs numériques, mais la complexité du système
ne nous permet pas, à l'heure actuelle, de réaliser un ajustement
de la sorte.
| 


