CHAPITRE II
THEORIE DE LA BARRE DE PRESSION DE HOPKINSON
DIVISEE
(BPHD)
II.1 Introduction
Il est essentiel de noter au début que pour faire la
dérivation des équations de gouvernement, on assume que les deux
barres cylindriques ont une même section constante (Ab) et sont de
même matériau isotrope. En outre, on suppose que les deux barres
ne subissent que des déformations élastiques.
II.2 Equation différentielle fondamentale de la
propagation d'onde
Dans n'importe quelle section différentielle de la barre,
le déplacement axial (ub) qui est fonction de la coordonnée(x) et
de temps (t) s'exprime ub = ub (x, t) .Un
élément de volume
différentiel de la barre est donné par
dVb = Abdx où dVb est
l'élément différentiel de volume
et dx est la longueur axiale différentielle. Comme la
section transversale est constante, c'est seulement la longueur axiale
différentielle qui détermine l'élément de volume
différentiel. Ecriture de l'équilibre des forces
appliquées sur ce volume différentiel comme illustré sur
la figure 2.1 donne:
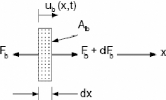
Figure II.1: Equilibre des forces pour les barres entrante(BE) et
sortante(BS) de l'appareil SHPB
? F r =mar
2
F (F
b b
+
+ = ñ
?
ub
2
dVb
? t
dF )
b b
? t
2
ñb
ub
?
2
dF b
(2.1)
A dx
b
|
est le vecteur force, m est la masse, ar est le
vecteur de l'accélération et Fb est la force
|
|
Où: F
|
appliquée dans la direction axiale à
l'élément de volume différentiel, et ñb
est la densité des barres.
La définition de la contrainte donne Fb =
óbAb et dF = d( ó A ) = d ó A +
ó dA
b b b b b b b

2
?
ub
2
? t
(2.2)
ub
Où: ób est la contrainte axiale dans la
barre. Comme la surface de chacune des deux barres est constante
(dAb = 0), le second terme s'annule. Ce qui donne:
dó b
Ab
ñ b
A dx
b
? 2
? 2 ub
? t 2
d dx
b
? t 2
ó= ñb
Comme les deux barres sont isotropes; subissant uniquement une
déformation élastique, la supposition d'un chargement uniaxial
donne la contrainte ainsi:
ó b = Ebåb (2.3)
Où: Eb est le module élastique isotrope
de la barre et åb est la déformation axiale dans la
barre. Il est aussi connu que la déformation axiale est donnée
par:
?ub
å = (2.4)
b ? x
Tel que åb = f(x,t)[16]. En correspondance,
la contrainte dans la barre doit être aussi une fonction de la position
et de temps et les différentiels totaux pour ób et x
dans l'équation (2.2) doivent être remplacés par des
différentiels partiels, ce qui donne:
?ó
? 2 u
b b
= ñ (2.5)
b 2
? t
x ?
La substitution de l'équation (2.3) dans l'équation
(2.5) en supposant que Eb est constant 0)
( =
? sur la longueur des barres réduit l'équation
(2.5) à:
Eb
2
?
ub
ñ b
2
? t
?x
?
? ? u ?

? x
b
b
? E ?
? ? x ?
?Eb
? x
?ub
? x
+ Eb
? 2 ub =
? t 2
ñ b
(2.6)
Eb
? 2 ? 2
u u
b b
=
2
2
ñb
? x?t
Equation (2.6) est l'équation différentielle aux
dérivées partielles fondamentale régissant la propagation
de l'onde de contrainte uniaxiale dans une barre élastique isotrope de
section constante [17].
II.3 Résolution de l'équation de
propagation de l'onde de contrainte
La solution analytique de l'équation (2.6),
associée avec d'Alembert, peut avoir la forme suivante correspondant
à la propagation de l'onde à gauche et à droite.
u (x , t) f (x c t) f (x c t) . (2.7)
b 1 b 2 b
= + + -
Où: f1 et f2 sont des fonctions arbitraires
déterminées à partir des conditions aux limites
et
initiales. c b est la vitesse de propagation de l'onde de contrainte dans
la barre [17].
L'introduction des variables ç = x + cbt et
æ = x - cbt simplifie l'équation (2.7) à:
u (x , t) u ( , ) f ( ) f ( ) (2.8)
b b 1 2
= ç æ = ç + æ
Maintenant, c'est relativement simple de trouver les
dérivées partielles de ub .Sachant que
?ç ?æ
= = 1, la première et la seconde dérivées
partielles de ub par rapport à x sont données
?x x
?
? u b
respectivement par:
df
(2.9)
1 2
df

= +
? x d ç d æ
2 2
?
d f
2 d f
u b 1 2
= + (2.10)
2 2 2
? x d ç d æ
Pour définir les dérivées de u b
par rapport au temps, on utilise:
?ç

?
t = cb
?æ ? =
?
et c b
t = - .Car c b est constant ?
? 0
c b b , les dérivées première et
deuxième
c ?
? =
? ? ? t ? x ?
de u b par rapport au temps sont respectivement
données par:
? u 1 2

b
? df df ?
= c ? - ? (2.11)
b
? t ? d ç d æ ?
2
? 2 u
2 ? d f
2
d f
b 1 2
2 b
= c ? +
? ? ç 2 æ 2
t d d
La substitution des équations (2.10) et (2.12) dans
l'équation (2.6) donne:
2 2 d f
2
E d f
b
? ? ? d f
2
d f ?
1 2 2 1 2
? + ? = ? +
?
2 b

c
ñ ç 2
? d æ ? ? ç 2 æ 2
d d d
b ?
.
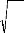
Eb
ñb
De l'équation (2.13), il est évident que la vitesse
de l'onde de contrainte est
? u ? u
b b
v v (x , t)
= = = #177; c
b b b
?t ? x
(2.14)
On note aussi que les équations (2.9) et (2.11) sont
conformées avec la solution de d'Alembert et donnent:
Où: vb (x, t) est la vitesse dans la barre
entrante ou sortante [17].
II.4 Développement des équations
régissant le spécimen
Etablissement de l'équilibre des forces dans la direction
x sur l'échantillon présenté à la figure II.2
mène à (Fg = Fd). Avec Fd est la
force appliquée sur sa face droite (interface
spécimen/barre sortante) et Fg est la force
appliquée sur la face gauche du spécimen (interface
spécimen/barre entrante). Il est important de noter que
ces forces et en conséquence les
contraintes et les
déformations sont dynamiques; elles changent avec le temps
(Fd, Fg = f(t)).
Cependant, l'hypothèse de l'équilibre est encore
valide tant qu'une précaution est prise pour s'assurer que les forces
sur l'une ou l'autre extrémité du spécimen (S) demeurent
équivalentes durant l'évènement dynamique.

Figure II.2: Equilibre des forces pour le spécimen dans le
dispositif BPHD
Sous les conditions d'équilibre dynamique, les forces
dans les barres entrante et sortante aux interfaces avec le spécimen
sont égales et opposées à ceux dans le spécimen
.Elles sont données par:
F (t) F (t) (t)A E A (t) (2.15)
g d b b b b b
= = ó = å
Où: åb (t) est la déformation
axiale "effective" dépendante de temps à
l'extrémité gauche ou
droite du spécimen. L'équation (2.15) permet aux
pulses de déformation incidente, réfléchie,
et
transmise dans les barres d'être utiliser comme
représentations des forces Fg (t) et Fd (t) dans
le
spécimen. Utilisant les déformations effectives
appropriées, l'équilibre de force est donné par:
F (t)
g F (t)
d
A E ( (t) (t)) A E (t) (2.16)
b b I R b b T
å + å = å
å T (t)
(t)
= å + å
I R
(t)
Où: åI (t), å R (t) et
åT (t) respectivement, les déformations axiales
dépendantes de temps:
incidente, réfléchie et transmise. On note que la
déformation effective à l'interface
barre
entrante/spécimen est la somme des déformations
incidente et réfléchie tandis que la
déformation effective à l'interface barre
sortante/spécimen est simplement la déformation transmise.
La contrainte moyenne dans le spécimen est donnée
par:
g d
+ A E
ó =
(t) = å + å + å
( (t) (t)
S b b
I R T
2A2A
F (t) F (t)
(t)) (2.17)
Où: A S est la surface de la section
transversale du spécimen
Comme le spécimen est en équilibre, la force
axiale appliquée au spécimen est donnée au choix par l'une
des deux forces de côtés. Pour la simplicité, puisque c'est
un seul terme, on prend celle de la face droite. Alors, on écrit:
F S (t) = Fd(t) = EbAbåb(t) (2.18)
Avec FS (t) est la force axiale dépendante de
temps agissant sur le spécimen. Par correspondance, la contrainte dans
le spécimen est donnée par:
(t) å
F (t) E A (t)
b b T
ó = =
S (2.19)
S A
A S S
Où: ó S (t) est la contrainte axiale
dépendante de temps dans le spécimen. Le taux de
déformation du spécimen est obtenu en dérivant par rapport
au temps la déformation.
d ? ? u b b
? ? u

å& = å =
(t) ( (t)) ( ) = ( ) (2.20)
S
S
dt ? t ? x ? x ? t
Avec å& S (t) est le taux de déformation
axiale dans le spécimen et å S (t) est la
déformation axiale dans le spécimen. Notons qu'ici u b
est supposé une fonction continue de position et de temps pour
échanger les dérivées partielles.
? ), permet l'écriture du taux de
Ä
? x Ä x

La discrétisation de l'équation (2.20) en x (
déformation du spécimen en termes de vitesses
à chaque extrémité du spécimen. La substitution de
cette relation dans l'équation (2.19) donne :
Ä
? u b
? ? u Ä v (t) v (t)
b g d
-
? t v(t)
å& = ( ) = (2.21)
S (t) =
? x ?t Äx LL
S S
Où: v(t) est la vitesse axiale dépendante de
temps à l'interface barre/spécimen, L S est la
longueur axiale du spécimen, v g (t) est la vitesse axiale
à l'extrémité gauche du spécimen, et vd
(t) est la vitesse axiale à l'extrémité droite du
spécimen.
L'équation (2.14) donne les vitesses à chaque
extrémité du spécimen comme étant les produits de
la vitesse de l'onde de contrainte dans la barre entrante ou sortante et la
déformation effective à l'interface barre/spécimen.
Donc:
vg (t) = cb (å I (t) -
å R (t)) (2.22)
vd(t) = cb å T(t)
(2.23)
La substitution des équations (2.22) et (2.23) dans
l'équation (2.2 1) donne:

v (t) v (t)
g d
-
å (t)
& S
c (å (t)
b I
å (t)
& S
L S
L S
å (t) å (t))
R T
-
(2.24)
La substitution de la relation de åT (t)
donnée par l'équation (2.16) réduit l'équation
(2.24) à:
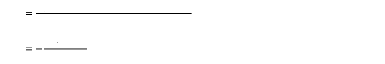
(t)))
+ å R
å (t)
& S
(t)
2c
å R
b
å (t)
& S
L S
c (å (t) å (t) (å (t)
b I R I
- -
L S
(2.25)
Par utilisation de l'équation (2.19), on peut trouver
la contrainte dans le spécimen en fonction de la déformation
transmise. Cependant, pour trouver la déformation dans le
spécimen, l'équation (2.25) doit être
intégrée pour donner:
t t 2c ( )
å ô 2c t
b
å = å ô ô = ?
(t) ( )d d ô = - å ô ô
( ) d . (2.26)
S 0 S
? & ? ?
b R
0 R
0L L
S S
Où: ô est un facteur d'intégration. Pour
un nombre discret de points de données, équation (2.26) est
modifiée de l'intégral à une sommation. Dans sa forme la
plus simple, l'approximation discrétisée de l'intégral est
donnée par:
N
2c t 2c
å = - å ô ô ? ? å Ä
b
(t) ? = ?
b
( ) d (2.27)
R i
t
S 0 R
L L
S S t 0
Avec å Ri est la valeur de la déformation
au temps donné par: ti = N Ä t.
La contrainte vraie et la déformation vraie,
respectivement ó V (t) et å V (t) , peuvent
être
obtenues à partir de la contrainte technologique et de la
déformation technologique (Engineering stress-strain) par la formulation
suivante [18]:

--
t)
(
(1
(t)
aV
c S
(t)
t))
(
t)) (
a S
c= -- -- c
V S
ln(1
(2.28)
II.5 Approches de validité de l'essai BPHD
Un essai BPHD valide nécessite la vérification
de certaines approches. Pour pouvoir utiliser les équations (2.19) et
(2.25) ou (2.26) dans le calcul du comportement contrainte- déformation
d'un spécimen sous un chargement à taux de déformation
élevé, à partir des quantités mesurées de
l'essai BPHD, il est important de satisfaire les approches/conditions ci-
après [49].
1) La propagation de l'onde de contrainte dans la barre est
1D. Les conditions qui satisfont cette approche nécessitent que les
barres soient:
a) homogènes et isotropes: Ceci peut être satisfait
par le choix convenable du matériau des barres.
b) uniformes dans la section transversale sur la longueur
entière et l'axe neutre est droit: Un usinage de précision des
barres (faible excentricité) peut assurer que la section transversale
est uniforme et l'axe neutre est droit.
c) sous un état élastique linéaire de
contrainte lorsqu'elles sont sollicitées par des pulses de contrainte:
Par le contrôle de la vitesse d'impact, il est possible de maintenir la
contrainte dans le pulse inférieure à la limite élastique
du matériau de la barre.
d) à distribution axiale uniforme de contrainte
à travers l'entière de la section transversale: Selon Davies [4],
un rapport (Lb/Db >20) entre la longueur de la barre (Lb) et son
diamètre (Db) satisfait cette condition.
e) exemptes des effets de dispersion: Cette approche
spécifique n'est pas valide pour les barres métalliques de grands
diamètres (diamètres supérieurs à 12 mm) ou les
barres viscoélastiques [15]. Les effets de dispersion sont à
corriger. Ils seront discutés dans le troisième chapitre.
2) Les interfaces barre entrante-spécimen et barre
sortante-spécimen restent planes à tout moment. Ceci peut
être satisfait, généralement, si:
a) Le spécimen est acoustiquement ductile; c.à.d,
il a une faible impédance acoustique (Figure II.3).
b) Le diamètre du spécimen est égale
à celui de la barre (ou bien légèrement inférieur
à celui de la barre comme mentionné par Kolsky [5]).
c) Un disque très dur est utilisé aux interfaces
barre-spécimen.
3) Le spécimen est en équilibre de contrainte
après une période initiale appelée " Sonner vers le haut
". La gamme de déformation où cette condition est satisfaite est
obtenue par comparaison des analyses 1D et 2D de l'onde. Une épaisseur
minimale possible peut minimiser le temps Sonner vers le haut (elle
dépend de la vitesse du son dans le spécimen), mais elle ne peut
pas l'éliminer.
4) Le spécimen n'est pas compressible. Cette condition
est facilement satisfaite; cependant, pour les mousses et les matériaux
non linéaires, des techniques d'analyse spéciales peuvent
être utilisées.
5) Frottement et effets d'inertie dans le spécimen
sont minimaux: Cette condition peut être satisfaite par lubrification des
interfaces barre-spécimen. Cependant, l'utilisation du lubrifiant peut
changer le comportement acoustique de l'interface.
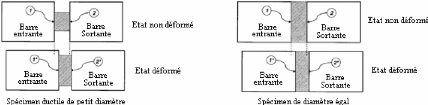
Figure II.3: Conditions pour des interfaces
barre-spécimen planaires. Les numéros 1 et 2 représentent
des interfaces BE-S et S-BS respectivement. Symbole * dénote l'endroit
des interfaces quand le spécimen est déformé [49].
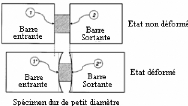
Figure II.4: Déformation des interfaces
barre-spécimen pour petit diamètre des spécimens
acoustiquement dur [49]
| 


