La déperdition des soins prénatals au Tchad

III.2 EVALUATION DE LA QUALITE DES DONNEES

Les données de l'EDST 1996-1997 comme celles issues de toute opération de collecte ne peuvent pas être exemptes d'erreurs. Il est important dès lors de procéder à une analyse permettant de fournir des indications qualitatives et quantitatives sur la confiance que l'on peut accorder aux résultats. Ceci peut déboucher sur la correction des données brutes voire sur un ajustement de données.

III.2.1 DETERMINATION DU TAUX DE NON REPONSE

En général, l'indicateur couramment calculé pour apprécier la qualité des données avant de tester toute autre méthode (graphique ou statistique) est le taux de non réponse. Les non réponses peuvent entraîner des biais considérables dans l'analyse des données. En général, le taux de non réponse est jugé acceptable quand il est inférieur à 10%.

Tableau 3.2 : Présentation des variables de l'étude et des taux de non réponse

Variables	Réponses valides	Valeurs manquantes	Taux de non réponse en pourcentage
Nombre de visites	1691	15	0,88
Age	1706	0	0,00
Parité	1706	0	0,00
Durée de la gestation à la 1^èreCPN	1696	10	0,59
Opportunité de la grossesse	1704	2	0,12
Niveau d'instruction	1706	0	0,00
Religion	1702	4	0,23
Région	1706	0	0,00
Ethnie	1706	0	0,00
Milieu de résidence	1706	0	0,00
Milieu de socialisation	1704	2	0,12
Distance	1559	147	8,62

Source : Traitement des données de l'EDST (1996-1997).

III.2.2 EVALUATION DE LA QUALITE DES DONNEES SUR L'AGE

Il existe plusieurs méthodes permettant de rendre compte de la qualité des données sur l'âge. On distingue d'une part la méthode d'évaluation graphique et d'autre part la méthode d'évaluation statistique.

III.2.2.1 METHODE D'EVALUATION GRAPHIQUE

Cette méthode consiste à disposer sur l'axe des abscisses des âges des personnes enquêtées et sur l'axe des ordonnées les effectifs. La distribution des individus par année permet ainsi d'avoir une idée sur la qualité des données recueillies. On s'attend à ce que la courbe de distribution de ces effectifs diminue régulièrement à mesure que l'âge augmente.

Graphique 3.1 Distribution des personnes enquêtées selon l'âge et le sexe.

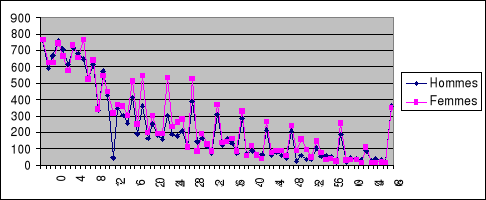
On observe sur le graphique ci-dessus une diminution des effectifs en « dents de scie ». Les saillies et les creux dénotent une mauvaise déclaration des âges. D'une manière générale, la population enquêtée a une préférence pour les âges se terminant par 0 et 5. Les âges ronds et semi- ronds sont plus attractifs chez le sexe féminin que le sexe masculin. Pour minimiser les biais que peuvent entraîner l'imprécision de la déclaration des âges dans l'interprétation des résultats, nous avons procédé à un regroupement des effectifs par groupes d'âges quinquennaux. Ce procédé a conduit à la construction d'une pyramide des âges (graphique 3.2) permettant d'analyser l'évolution des structures par âge des deux sous-populations (masculine et féminine). La pyramide des âges est un instrument privilégié de l'analyse de la qualité des données. Car la répartition par sexe et par âge d'une population obéit à certaines règles (Gendreau, 1993).

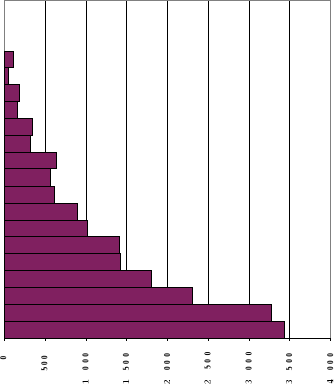
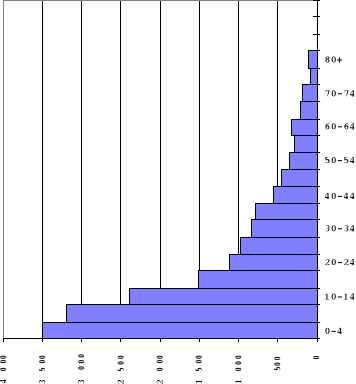
Graphique 3.2 : Pyramide des âges de la population enquêtée.

En construisant regroupant les effectifs par grands groupes d'âges, nous avons résolu en partie les problèmes liés à la mauvaise déclaration des âges (attraction pour certains âges et répulsion pour d'autres). La pyramide des âges ainsi construite présente une allure presque régulière, caractéristique des pays à fécondité et mortalité élevées : une base large qui se rétrécit rapidement avec l'âge. Par ailleurs, on peut signaler également un léger déséquilibre entre les deux sexes, notamment chez les adultes de 15-49 ans au détriment des hommes qui sont relativement moins nombreux que les femmes issues de la même tranche d'âges. La distribution de la population par groupes d'âges quinquennaux se caractérise par une proportion importante des jeunes de moins de 15 ans représentant près de la moitié de la population totale. Les personnes âgées de 15-64 ans représentent 47% et de 65 ans et plus ne correspondent qu'à une faible proportion (3%). Cette répartition de la population par grands groupes d'âges est pratiquement la même que celle trouvée au RGPH de 1993, ce qui rend compte de la bonne représentativité de l'échantillon de l'enquête EDS.

III.2.2.2 METHODE D'EVALUATION GRAPHIQUE

Plusieurs indices permettent de déceler l'attraction ou la répulsion de certains âges, ou mesurer la régularité, ou de mesurer la régularité de répartition par sexe et par âge. Les indices les plus couramment calculés sont : l'indice de Whipple, l'indice de Myers, l'indice de Bachi et l'indice combiné des Nations Unies. Seuls les trois premiers indices sont calculés dans le cadre de l'évaluation des données par la méthode statistique en recourant à la procédure SINGAGE du Logiciel PAS.

III.2.2.2. a INDICE DE WHIPPLE 

C'est l'indice le plus simple à calculer manuellement. Il mesure l'attraction ou la répulsion des âges ronds et semi-ronds en compensant l'effet dû à la décroissance normale des effectifs dans les groupes d'âges successifs. Il est calculé en rapportant à l'effectif des 23-62 ans, l'effectif de personnes d'âges se terminant par 0 ou 5 entre ces limites, et en multipliant le résultat par 5.

Si tous les âges enregistrés se terminent par 0 ou 5, l'Indice vaut 5 ; s'il n y a aucune attraction ou répulsion pour ces âges, il vaut 1 ; s'il y a contraire répulsion pour ces âges, il est inférieur à 1 et vaut 0 si aucun âge ne se termine par 5 (Gendreau, 1993). L'avantage de cet indice est sa simplicité. Son inconvénient est de ne mesurer que la préférence pour les chiffres 0 et 5.

On trouvera dans le tableau 3.2 ci-dessous le calcul de l'indice de Whipple (I_W). D'une manière générale, on note une mauvaise qualité de la déclarations des âges pour l'ensemble de la population enquêtée (I_W=2,12). La population enquêtée a tendance à préférer les âges se terminant par 0 et 5. On constate que la qualité de la déclaration des âges pour le sexe masculin est relativement meilleure pour le sexe féminin. Cette situation peut être imputable au faible niveau d'instruction observé chez les femmes par rapport aux hommes.

III.2.2.2.b INDICE DE MYERS

L'indice de Myers (I_M) traduit les préférences (ou aversions) pour les âges se terminant par chacun des chiffres de 0 à 9. Il est compris entre 0 et 180. L'indice de Myers est nul si les déclarations d'âge sont exactes. Sa valeur est d'autant plus élevée que les préférences ou aversions pour les âges se terminant par certains chiffres sont plus grandes. Sa valeur maximale est atteinte lorsqu'il y a préférence pour tous les âges se terminant par un même chiffre, et vaut 180 (ibid.).

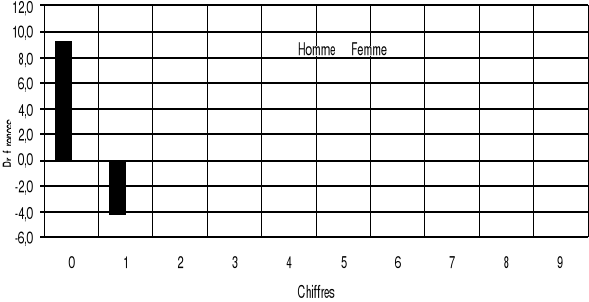
L'indice de Myers est de 35,5 pour l'ensemble des deux sexes, 31,8 pour le sexe masculin et 38,6 pour le sexe féminin. Cette situation illustre bien les préférences ou aversions pour certains âges. Bien que la qualité de la déclaration des âges soit mauvaise, le rapprochement de différents indices de Myers 0 par rapport à 180 permet d'admettre les données sur l'âge comme acceptables. Comme l'indice de Whipple, l'indice de Myers confirme l'attraction qu'il y a pour les âges ronds et semi-ronds pour l'ensemble de la population enquêtée quel que soit le sexe. D'un autre côté, on constate une répulsion pour les âges se terminant par les chiffres 1, 3,4 et 9 pour l'ensemble des deux sexes, le sexe masculin et le sexe féminin.

Graphique 3.3 : Evaluation graphique de la qualité de l'âge (Méthode de Myers).

III.2.2.2.c L'INDICE DE BACHI

L'indice de Bachi (I_B) varie entre 0 et 90. I_B=0, lorsqu'il y a aucune préférence ou aversion. I_B= 90, lorsque tous les âges déclarés se terminent par le même chiffre. D'une manière générale, les résultats illustrés par le graphique ci-dessous, sont peu différents de ceux fournis par l'indice de Myers. On remarque que les personnes enquêtées ont une préférence pour les âges ronds et semi-ronds. Cependant, les âges se terminant par 1 ; 9 ; 4 ; 3 ; 6 7, 2 et 8 n'exercent pas d'attrait suivant un ordre d'importance.

Graphique 3.4 : Evaluation graphique de la qualité de l'âge (Méthode de Bachi).

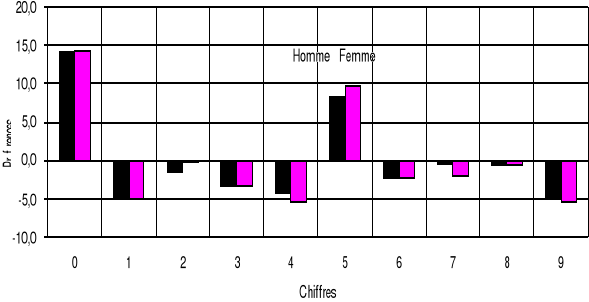
Tableau 3.3 Calcul des indices de Whipple, de Myers et Bachi.

	Hommes	Femmes	Ensemble
Indice de Whipple	2,06	2,17	2,12
Indice de Myers	31,8	38,6	35,5
0	9,2	10,8	10,1
1	-4,3	-4,5	-4,4
2	-0,1	-0,1	-0,1
3	-2,4	-2,7	-2,5
4	-2,6	-4,4	-3,6
5	5,7	7,3	6,6
6	-1,6	-1,7	-1,6
7	-0,8	-1,7	-1,3
8	1,0	1,1	1,0
9	-4,2	-4,3	-4,3
Indice de Bachi	22,2	24,2	23,4
0	14,0	14,3	14,2
1	-4,9	-5,1	-5,0
2	-1,6	-0,2	-0,8
3	-3,4	-3,4	-3,4
4	-4,4	-5,4	-4,9
5	8,3	9,6	9,0
6	-2,1	-2,2	-2,2
7	-0,4	-2,0	-1,3
8	-0,6	-0,7	-0,6
9	-4,8	-5,4	-5,4

Source : Traitement des données de l'EDST (1996-1997).