CHAPITRE I
Notions fondamentales de géodésie
physique
Le problème fondamental de la géodésie
physique est de déterminer la surface équipotentielle du champ de
pesanteur terrestre coïncidant avec le niveau moyen des mers et servant de
référence pour la définition des différents
systèmes d'altitudes utilisés lors de levés
géodésiques. Cette surface est connue sous le nom de
géoïde. Son comportement dépend des caractéristiques
du champ de pesanteur dont les déformations sont causées par
l'existence de masses internes de différentes densités.
I.1 Potentiel de pesanteur terrestre
On considère le système fondamental terrestre
orthonormé (XYZ) d'origine O, confondue avec le centre
de gravité de la Terre (géocentre), dont l'axe OZ
coïncide avec l'axe moyen de la rotation de la Terre dirigé vers le
pôle nord. L'axe OX est contenu dans le plan méridien de
Greenwich et l'axe OY est orienté de manière à ce
que le système (XYZ) soit orthonormé et direct.
Une quantité de base décrivant le champ de
pesanteur terrestre est le potentiel de pesanteur W (rt). Ce potentiel
est défini comme suit :
W(rt) = V(rt)+t7i(rt) (1.1)
où V(rt) est le potentiel gravitationnel.
t7i(rt) est le potentiel centrifuge.
rt est le rayon géocentrique de la Terre.
Le potentiel de pesanteur W(rt) satisfait aux relations
suivantes :
2w2 à l'extérieur de
SE
AW(rt) =
-4vGp + 2w2 à l'intérieur de
SE
A : opérateur Laplacien ;
SE : surface topographique ;
w : vitesse angulaire de la Terre ;
ñ : densité de masse de la Terre ;
G : constante de la gravité newtonienne
(G = 6.672
x10-11m3s-2kg-1).
Le vecteur pesanteur ?g est défini dans le
système (O, XYZ), par le gradient de W(rt), tel que
:
? = W= t r?W ? W
?W)
g grad "
l?X , ?Y , ?Z ),
t ??W ?W ? W ?
avec ?
? , , représentant la transposée du vecteur
ligne ? ? W ? W ? ?
W .
? ? X ? Y ? Z , ,
? ? ?
? ? x ? y ??
z
Les surfaces dont le potentiel W(rt) est constant
(W(rt)=Const.) sont appelées "surfaces équipotentielles"
ou "surfaces de niveau". Elles sont, en tout point, orthogonales au vecteur
pesanteur ?g . Le géoïde
Sg dont le potentiel W(X, Y, Z)=W0=Const. est
considéré comme la
surface de référence de ces
surfaces ; il représente, physiquement,la surface moyenne des
océans.
Soit P un point à la surface SE, la
distance de ce point au géoïde Sg, le long de
la verticale, est l'altitude orthométrique To du
point P (Fig I.1).
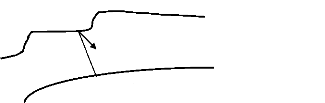
P
SE (surf. Topographique)
n
Ho
Sg (surf. Géoïde)
P0
Figure I .1 : Altitude orthométrique
Ho.
I.2 Champ de pesanteur normal
Le champ de pesanteur normal représente un
modèle théorique du champ de pesanteur réel ; il est
généré par un ellipsoïde de révolution, dont
les dimensions, la masse et la vitesse de rotation sont respectivement, proches
des dimensions, de la masse et de la vitesse de rotation de la Terre. Il est
choisi tel que son centre coïncide avec le centre de gravité de la
Terre, cet ellipsoïde est appelé ellipsoïde de
référence.
Il existe plusieurs ellipsoïdes de références.
Le plus répandu est l'ellipsoïde WGS-84 et il est
défini à l'aide des paramètres suivants :
Le demi-grand axe ae = 6378137 m.
Le demi-petit axe be = 6356752 m. La vitesse
angulaire ù = 7292115x10-11 rad
s-1.
La valeur du potentiel de pesanteur théorique de
l'ellipsoïde de référence WGS84 est:
U0=62636860.8497m2s-2.
Un autre paramètre important est la première
excentricité "e" définie par :
1
e = ?
b 2 2
? - ?
e
? 1
? a 2 e ?
L'évaluation du potentiel de pesanteur normal
U(rt) et de la pesanteur normale ã à l'extérieur
de l'ellipsoïde de référence dépend de la
connaissance de ces quatre quantités ae,
be,ù et U0 [Heiskanen et al.,
1967].
U satisfait : ?U(rt) =
2ù2 à l'extérieur de
Se
-4ðGñN + 2ù2 à
l'intérieur de Se
oil Se est la surface de l'ellipsoïde de
référence et ñN est la densité normale.
Les surfaces U(rt) = Const. sont les surfaces de niveau
normales et la direction normale est déterminée par la direction
de pesanteur normale ãr . La distance h, compté
le long de la
normale à l'ellipsoïde et passant par P,
entre le point P et l'ellipsoïde de référence est
appelée « altitude ellipsoïdale », (Fig.I.2).
Le telluroïde St, surface
géométriquement proche de la surface topographique est
définie par l'ensemble des points Q obtenus par la projection
des points P situés sur la surface topographique le long de la
direction normale (Fig. 1.2).
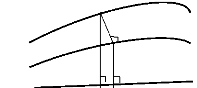
SE (Topographique)
P
·
Ho
Sg (Géoïde)
h
N
Se (Ellipsoïde)
Se
·
·
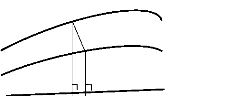
SE (Topographique)
P
St (Telluroïde)
Se (Ellipsoïde)
·
æ
Q
h
H
·
·
Figure I.2 : ondulation du géoïde
N et anomalie de hauteur æ
La distance d'un point sur la surface St à
l'ellipsoïde Se le long de la normale à
l'ellipsoïde de révolution est l'altitude normale
HN du point P correspondant (Fig. 1.2).
La distance géométrique séparant le
géoïde et l'ellipsoïde, et comptée le long de la
normale à l'ellipsoïde de référence est
exprimée par la hauteur du géoïde (ou l'ondulation du
géoïde) N (Fig. 1.2) ; elle est donnée par la
formule de Bruns:
N = h - Ho =
T( rt) (1.2)
ã
La différence géométrique, comptée
le long de la normale à l'ellipsoïde de référence,
entre la surface topographique et le telluroide est appelée «
anomalie de hauteur æ ». (Fig. 1.2). Elle est exprimée par la
formule :
æ = h - HN (1.3)
I.3 Potentiel perturbateur
Le potentiel perturbateur T(rt) est donné par la
différence entre le potentiel de pesanteur W(rt) et le
potentiel de pesanteur normal U(rt):
T(rt) = W(rt) - U(rt) (1.4)
Puisque la densité des masses à
l'extérieur de la surface terrestre est supposée nulle,
T(rt) satisfait à la condition d'harmonicité à
l'extérieur de la surface topographique et vérifie, ainsi,
l'équation de Laplace :
?T(rt) = 0 (1.5)
La différence entre la pesanteur réelle et la
pesanteur normale peut être exprimée de deux façons
différentes en fonction de la pesanteur normale:
La perturbation de pesanteur (äg) est
donnée par la différence entre la pesanteur (gp) et la
pesanteur normale au même point (ãp) :
äg(rt) = gp(rt)-ãp(rt) (1.6)
L'anomalie de pesanteur (?g) est définie par
la différence entre la pesanteur au point P (gp) et la
pesanteur normale (ãQ) au point Q (la projection du
point P suivant la normale à l'ellipsoïde de
référence sur le telleroïde) :
?g(rt)= gp(rt)-ãQ(rt) (1.7)
Les objectifs principaux de la géodésie physique
sont la détermination du champ de pesanteur et du géoïde.
Cependant le champ de pesanteur normal peut être directement
évalué à partir d'expressions mathématiques simples
; les problèmes sont donc convertis en la détermination du
potentiel perturbateur T(rt) et de la hauteur du
géoïde N ou de l'anomalie de hauteur æ qui sont
relativement petits. Les données utilisées sont les
quantités du champ de pesanteur mesurées à la surface de
la Terre. Le problème de base de la géodésie physique peut
être exprimé par un problème de valeurs aux limites
géodésiques
I.4 Problème de valeur aux limites
géodésique
Le problème de valeur aux limites
géodésique (BVP: Boundary Value Problem) joue un rôle
fondamental dans la théorie du calcul du géoïde et de son
application. On appelle Ó la surface limite. Un problème
de valeur aux limites en géodésie physique peut être
exprimé comme suit :


?T = 0 à l'extérieur de
Ó
BT = f sur Ó
T = O(r-1) à l'infini

T est le potentiel perturbateur, B est un
opérateur défini sur la surface limite Ó, et
f est une fonction définie sur Ó et provient
des différentes mesures gravimétriques, observation de
nivellement, les systèmes de positionnement globaux (GPS), etc. ....
Généralement, Ó est
l'ellipsoïde de référence, le géoïde ou la
surface de la Terre, et B distingue les opérateurs de
Dirichlet, Neumann ou le problème mixte selon la formulation du BVP
convenant à l'étude [Zhiling Fei 2000].
Selon les différences des données, on énonce
le problème de valeurs aux limites géodésiques sous
diverses formes:
(1) Problème de 1ère
espèce (Dirichlet):
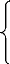
?T = 0 à l'extérieur de
Ó
T = W - U sur Ó
T = O(r-1) à l'infini
Les données de ce problème sont le potentiel de
pesanteur terrestre W sur la surface Ó
(Ó= SE).
(2) Problème de 2ème
espèce (Neumann):
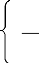
?T = 0 à l'extérieur de
Ó
?T sur Ó
? h
T = O(r-1) à l'infini
= - äg
où ?(.) représente la dérivée
normale.
?h
Dans ce cas, les données sont la pesanteur g
à la surface topographique SE, qui peut être obtenue
par les mesures GPS et gravimétriques.
(3) Le problème de 3ème
espèce (mixte) :
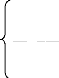
?T = 0 à l'extérieur de
Ó
? T - 1 ?ã T = -?
g
?h ã ?h
sur Ó
T = O(r-1) à l'infini
Les données sont le potentiel de pesanteur W
et la pesanteur g sur la surface SE, qui est obtenue
à partir des mesures gravimétriques et nivellement. Ce
problème représente le problème fondamental de la
géodésie physique dont la formulation est donnée, selon
l'approche de Stokes [Heiskanen et al.1967] par l'équation :
T (rt ) + ?g
(rt ) 0
(1.8)
(1.9)
?T (rt ) 1 ?ã
?h ã ?h
où T est le potentiel perturbateur et
?g est l'anomalie de pesanteur.
Une approximation sphérique à cette équation
est donnée par :
? T (rt ) +
2 T r
( ) ( ) 0
+ ? g r =
?
r R
t t
où R est le rayon moyen de la Terre défini
par : R = 3
a2eb e et ae
, be sont les demigrand axe et demi-petit axe, respectivement, de
l'ellipsoïde de référence.
T (r t)
? - g(rt )
+ã(rt ) + å äg
(rt ) = -äg(rt )
+ åäg(rt) .
?
?r
(1.10)
åäg (rt) est la correction ellipsoïdale
à la perturbation de pesanteur, due au remplacement de la
dérivée normale par la dérivée radiale :
f ? T
åä g ( t ) sin 2
r = ? + Ï ( 2 )
R ? ?
f (1.11)
où f est l'aplatissement
géométrique donné par:
La solution du 3éme problème consiste
à déterminer le potentiel perturbateur T sur le
géoïde par la résolution de l'équation de Laplace
(1.5) sous la condition de la formule fondamentale (1.8) et en connaissant les
valeurs des anomalies de pesanteur ?g sur le géoïde. Sous
ces conditions, il peut être ramené à un problème de
valeurs aux limites de première espèce de la théorie du
potentiel (ou problème de Dirichlet) en considérant le
géoïde comme surface de référence.
Toutefois nous relevons deux importantes objections à
cette théorie. D'une part le manque de précision de la
densité des masses topographiques entre le géoïde et la
surface topographique ne permet pas au potentiel perturbateur de satisfaire
à l'équation de Laplace. D'autre part, nous ne connaissons pas la
valeur de la pesanteur au niveau du géoïde.
Rappelons que les mesures de pesanteur sont effectuées
à la surface du sol ou à une certaine hauteur de celui-ci ; ce
qui nous amène à utiliser une méthode de réduction
pour le calcul de la pesanteur au géoïde. Cependant le manque
d'informations précises sur la densité de la masse topographique
ne permet pas de calculer correctement la pesanteur au niveau du
géoïde. Pour pallier à ces inconvénients ; plusieurs
approches ont été proposées dont la méthode de
Helmert [Helmert, 1884] que nous décrirons en détails dans le
chapitre qui suit.


| 


