I.3.2 Voltammétrie à onde carré
(VOC)
La voltammétrie à onde carrée est
basée sur la combinaison d'une modulation d'onde carrée
d'amplitude avec une rampe en escalier. Le signal mesuré est la
différence Ai entre les courants mesurés à la fin de
chaque pulse montant et descendant de l'onde carrée (Daamouche, 2009)
.La figure 6 schématise la forme de potentiel appliquée dans le
cas de la VOC.
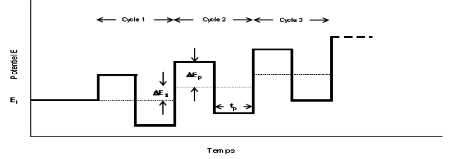
Thèse de" Master of Science " de TAGNE TIEGAM RUFIS 32
Figure 4 : Allure de la commande
de potentiel imposé en fonction du temps en voltammétrie à
ondes carrées.
Les paramètres caractéristiques de la
voltammétrie à onde carrée sont : - ÄES :
incrément de potentiel au début de chaque cycle.
- ÄEP : amplitude d'une demi-période
La voltammétrie à onde carré a l'avantage
supplémentaire d'être plus rapide que les méthodes
conventionnelles à impulsion différentielle, permettant ainsi de
réduire les durées d'analyse. En effet, alors qu'en
voltammétrie à impulsion différentielle les vitesses de
balayage varient de 1 à 10 mV/s, la voltammétrie à onde
carré autorise des vitesses de balayage de plus de 1 V/s.
I.3.4 La spectroscopie d'impédance
électrochimique (SIE)
La spectroscopie d'impédance électrochimique
« STE » est une technique non destructive adaptée à
l'étude des propriétés électriques interfaciales
(Monk et al., 2008). Elle permet de différencier les divers
phénomènes susceptibles de se produire dans la cellule
électrochimique en fonction de la fréquence : les
phénomènes rapides se produisent à hautes
fréquences, tandis que les phénomènes lents ont lieu
à basses fréquences (Ribaut, 2008).
La STE repose sur la mesure d'une fonction de transfert suite
à la perturbation volontaire du système électrochimique
étudié. Ce système peut être considéré
comme étant une « boîte noire »qui réagit en
émettant un signal y(t) quand il est soumis à une perturbation
x(t) (figure 7). Les deux signaux x(t) et y(t) sont alors reliés par une
fonction de transfert 11(w) telle que Y (w) = 11(w) X(w), X(w) et Y (w)
étant respectivement les transformées de Fourier de x(t) et y(t)
(Yang et al. ,1994).

Thèse de" Master of Science " de TAGNE TIEGAM RUFIS 33
Figure 5 : Une fonction de
transfert.
Classiquement, la perturbation imposée est
sinusoïdale. Le signal appliqué est donc de la forme x(t) = A sin
(wt) et la réponse du système est y(t) = B sin (wt+ (p) avec une
fréquence f, une pulsation w = 2ðf et un déphasage (p.
L'impédance électrochimique se définie comme étant
le nombre complexe Z (w) résultant du rapport :
1 Zj
? ? tan?
(I-9)
Où, en mode potentiostatique, ?E(w) est la perturbation
imposée à un potentiel choisi E0, et ?I (w) la réponse en
courant du système étudié avec une composante continue I0
. Il est aussi possible d'utiliser le mode galvanostatique. Dans ce cas, c'est
une perturbation en courant de faible amplitude qui est appliquée au
système et c'est la réponse en potentiel qui est mesurée.
L'impédance Z(w) est un nombre complexe qui peut être écrit
sous deux formes équivalentes :
Z (w) = |Z (w)| ej(p(w) ou Z (w) = Zr(w) + jZj(w) avec
, (I-10)
|Z | étant le module de l'impédance, (p le
déphasage, Zr la partie réelle et Zj la partie imaginaire.
Pour passer d'une forme à l'autre, il suffit d'utiliser
les relations suivantes :
|Z |2= Z2r+ Z2j et
Zr ou Zr = |Z | cos (p et Zj = |Z | sin (p ...
(I-11)
L'impédance d'un système électrochimique,
quel qu'il soit, peut en effet être assimilée par analogie
à une impédance électrique. On peut donc associer à
ce système un circuit électrique équivalent ou (CEE)
où chaque phénomène physico-chimique se déroulant
à l'interface électrode/électrolyte peut être
modélisé par un composant électrique.
| 


