Education et croissance économique en Algérie: Une analyse en terme de causalité à l'aide des modèles VAR

CHAPITRE III

ÉTUDE ÉCONOMETRIQUE

« Un modèle n'est jamais juste, il est juste utile »

B.F

Introduction :

L'analyse de l'évolution du système éducatif Algérien du chapitre1 a mis en évidence les efforts considérables consentis par l'Etat Algérien à l'éducation. Néanmoins, la revue de littérature empirique du chapitre 2 montre qu'il y a un débat concernant l'effet de l'éducation sur la croissance économique.

Le but de cette étude économétrique est d'étudier les liaisons entre la croissance économique et les variables éducatives pour le cas de l'Algérie. La première section rappelle les définitions et les principales propriétés des processus aléatoires univariés et multivariés. La seconde section présente les variables utilisées, et commente les principaux résultas.

SECTION 1 : Processus aléatoires et représentation VAR.

Nous rappelons tout d'abord en (1.1) les définitions et les principales propriétés des processus aléatoires stationnaires et non stationnaires. Puis nous présentons en (1.2) la modélisation multivariée et la notion de cointégration.

1.1. Généralités sur les processus aléatoires univariés : 1.1.a. Notions et Définitions :

1. Processus Aléatoire :

Un processus aléatoire est une suite de variables aléatoires indexées dans le temps et définies sur un espace des états de la nature. Ainsi, pour chaque instant du temps, la valeur de la quantité étudiée X_t est appelée variable aléatoire et l'ensemble des valeurs X_t quand t varie est appelé processus

aléatoire

2. Série Chronologique :

En économie, les données constituent souvent des séries d'observations sur une ou plusieurs variables faites à différentes dates : les observations ne sont pas indépendantes.

On appelle série chronologique (ou série temporelle) toute suite d'observations (X_t, t ? T) indexées par un ensemble ordonné T (le « temps »).

Types de Séries :

Une série chronologique ou encore chronique est un ensemble d'observations d'un processus aléatoire (Xt)t?T se réalisant en un instant spécifié t ? T.

· Série continue: Une série chronologique est dite continue si l'ensemble des instants d'observations est continu (non dénombrable).

· Série discrète: Une série chronologique est dite discrète si l'ensemble des instants d'observations est discret (dénombrable).

1.1.b. Processus Aléatoire stationnaire :

1. Stationnarité Stricte et Stationnarité faible :

Nous commencerons par poser la définition d'un processus stationnaire au sens strict (ou stationnarité forte) et par là étudier ensuite les propriétés de la stationnarité du second ordre (ou stationnarité faible).

Le processus aléatoire (X_t, t ? T) est dit strictement stationnaire si :

? i=1 ,..., n avec t₁ < t₂ <...< t _n tel que t_i?T et h ? T avec t_i+h ? T, les deux suites (x t 1 ,... , x _tn ) et (xt 1+h,..., xtn +h) ont la même loi de probabilité.

Autrement dit :

? (x₁ ,..., x_n ), ? (t1,..., t_n) et ? h ? T : P [xt 1 < x₁ ..., x _tn <x_n ] = P [x t 1+h < x ₁ ,..., xtn +h <x_n ].

Le processus aléatoire (X_t, t? T) serra dit stationnaire au sens faible, s'il aura une moyenne et une

variance qui ne changeront pas avec le temps, et si la covariance entre les valeurs du processus en deux points dans le temps ne va dépendre que de la distance entre les points dans le temps et non du temps lui-même. C'est à dire :

1. 2. 3.

E (X t ) = ì < 8 + 2 Var (X t ) = ó Cov(X t ,X t+h)=( h)

? t ? T; ? t ? T; ? t, h ? T .

En résumé, un processus est stationnaire au second ordre si l'ensemble de ses moments sont indépendants du temps.

2. Processus Bruit Blanc (White Noise):

Parmi la classe des processus stationnaires, il existe des processus particuliers que sont les processus bruit blanc (ou White Noise). Ces processus sont très souvent utilisés en analyse des séries temporelles, car ils constituent en quelque sorte les »briques élémentaires» de l'ensemble des processus temporels. Tout processus stationnaire peut s'écrire comme une somme pondérée de bruits blancs (théorème de Wold).

Le processus {å _t ,t ? Z} est dit un bruit blanc faible noté ( ) 2

å t~wn(0,ó _å ) si:

3. E(å _t )=0,?t? Z. 3. V(å _t )=ó _å 2,?t?Z.

ó ² 0.

si h =

å

3. ( )

COV E h

( , ) ( )

å å - å å - í

= = =

t t h t t h ^å 0 0.

? ?

h

Le processus { å _t , t ? Z} est dit un bruit blanc fort s'il est indépendant et identiquement distribué (i.i. d). Si le bruit blanc (å_t) est normalement distribué, on parle de bruit blanc Gaussien :

å t ~ Í 0, ó å

( ² )

3. Fonction d'Autocovariance : La fonction d'autocovariance du processus aléatoire (X_t ,t ? T ) mesure la covariance pour un couple de

valeurs séparées par un intervalle de longueur h appelé retard, elle fournit des informations sur la variabilité de la série et sur les liaisons temporelles qui existent entre les différentes composantes de la série Xt .

Définition : La fonction d'autocovariance du processuus {X_t ,t? T } est définie :

í : T * T ? IR

(t , s) ? í (t, s)= Cov (X t, X _s)

= E [ (X _t - E (X t)) (X s - E (X _s )) ] ? t, s ? T Estimation de la fonction d'autocovariance :

Considérons un ensemble d'observations X₁,... ,X_n. Issues d'un processus (X_t ,t? Z ) La moyenne empirique est donnée par :

t

1 ⁿ

X X

=

n =

1

t

La fonction d'autocovariance empirique est donnée par :

t = 1

n h

-

= - -

( )( )

X X X X

t t h

-

, h +

? ? Z .

í à( )

h

1

n h

-

ñ ? ñ

à

t N 0,1 h

ñ h ( ) ( )

= ? ? ?

h h

V ñ à h

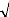
Cet estimateur est biaisé mais il est asymptotiquement sans biais.

4. La fonction d'autocorrélation (AC):

La fonction d'autocorrélation notée ñ(h) mesure la corrélation de la série avec elle-même décalée de

h périodes.

On supposera par la suite que le processus {X_t ,t ? Z } est stationnaire du second ordre. Définition :

On définit la fonction d'autocorrélation par la formulation suivante :

ñ(h)= Corr ( Xt , Xt-h) =

í h

( )

= (0)

í

, ?h? Z.

COV X X

( )

t , t h

-

VAR X VAR X

( ) ( )

t t h

-

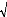
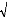
Cette fonction ñ(h) est à valeurs dans[-1,+1] .Sa représentation graphique est appelée corrélogramme. Propriétés: La fonction d'autocorrélation d'un processus (Xt ) stationnaire vérifie :

· ñ(0)= 1;

· ñ(h) = ñ(0) ;

· ñ(h) = ñ(-h) (c'est une fonction paire).

Estimation de la fonction d'autocorrélation :

La fonction d'autocorrélation empirique est donnée par : ( )

à h

ñ í

h í

à( ) à 0

= ? h ? Z

( )

Cet estimateur est biaisé, mais il est asymptotiquement sans biais.

D'après le théorème central limite, la variable centré ñh

t suit une loi normale réduite :

où V (àñ_h) désigne l'estimateur de la variance empirique des estimateurs ñà_h:

h - 1

( )

ñ à h

ñ ²

j

n j = -

V

1

=

à

( 1)

h -

En utilisant la symétrie des ñ_h , on obtient :

h - 1

V ( )

ñ à h

(1 2 à )

ñ ²

= + j

j 1

1

n

la statistique de Student associée au test H₀: ñ_h = 0, est donnée par :

?Z

ñ à

t N 0,1 h

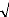
ñ h ( ) ( )

= ? ?

h

V ñ à h

au seuil	á= 5%, si	tñàh		= 1.96, on rejette l'hypothèse H0, c'est à dire la nullité de ñh.

5. Fonction d'Autocorrélation Partielle (PAC) :

Définition :

La fonction d'autocorrélation partielle de retard h notée ø(h) , mesure la corrélation entre X _t et Xt - h

une fois retirée l'influence des variables antérieures àX t - h.

R h

ø = ? ?Z

( ) , .

h h

R h

( )

* ( )

La fonction d'autocorrélation partielle est donné par :

La représentation graphique de cette fonction est appelée corrélogramme partiel. avec :

1 (1) ( 2) ( 1)

ñ ñ ñ

h h

- -

ñ(1) 1( 2)

? ? ñ h -

=

R h

( )

? ? ?

ñ ( 2) 1 (1)

h - ? ? ñ

ñ ñ ñ

( 1) ( 2) (1) 1

h h

- -

et on introduit de façon analogue la matrice R * ( h ) obtenue en remplaçant la dernière colonne de R ( h ) par le vecteur [ ]'

ñ (1), , ñ ( h ) .

1 (1) ( 2) 1

ñ ñ h -

ñ ( )

1 1 ? ? ñ ( )

1

R h

*( ) = ? ? ñ (1)

ñ ( )

h - 2 1 ( 1)

? ? ñ h -

ñ ñ ñ ñ

( 1) ( 2) (1) ( )

h h

- - h

Estimation de la Fonction d'Autocorrélation:

-Un estimateur naturel øà h de l'autocorrélation partielle ø_h du processus (X_t, t ?Z) consiste en l'estimateur des MCO du dernier paramètre de la régression :

X + c ø X ø X ø _h X t h å t h

t à à t à t à 1 à ,

1 1 2 1

= + + + + - + + ? ?Z

-

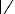
-On peut également utiliser la relation : à ( ) ( ) ( )

ø = R h R h h

h à * à , ? ? Z

6. Les Opérateurs Linéaires :

Opérateurs de Retard et d'Avance:

On considère le processus stochastique (aléatoire) stationnaire {X_t ,t ? Z } .

Définitions :

· On appelle opérateur retard L (L =lag, ou B =backward) l'opérateur linéaire défini par

L : X t ? L (X_t) = LX t = X t-1

· On appelle et opérateur avance F (F =forward) l'opérateur linéaire défini par

F : X t ? F (X_t) = FX t = X t+1

Propriétés :

1. L² = L o L, et plus généralement, L j = LoLo~~~~~~~ oL,j ? N.

j fois

2. L ^j X t = X _t-j, ? j ? Z , en particulier on a 0 L X t = X _t .

3. Si X = C, ? t ? a v ec C ? R , L X t = L C = C , j .

Z ? ?

j ^j Z

t

4. i j i+ j

L(LX _t )= L X t = X _t-i-j , ? ( i, j) ? Z .

2

5. L o F = F o L = I (opérateur identité) et on note -1

F = L et -1

L = F .

6. -j j

L = F pour j? N.

Opérateur de Différence :

On considère le processus stochastique {X_t ,t ? Z } non stationnaire, pour le rendre stationnaire on utilise des opérateurs de différentiation et de désaisonnalisation.

1. ÄX t = (1 - L) X t = X _t - X _t-1 , opérateur de différentiation (première différence).

2. j j

Ä X t = (1 - L) X _t pour tout j N,

? opérateur de différentiation.

Ä _S Xt = (1 - L ) X t = X _t - X _t-s, opérateur de désaisonnalisation.

7. Processus MA et AR :

Processus MA :

Le processus (X_t, t ? Z) satisfait une représentation MA d'ordre q, notée MA(q), si et seulement si :

q

è L ^j

= j

.

X = m+ È (L) å t

t

avec E (X_t) = m ,le polynôme È (L) étant défini par : ( )

È L

j 0

où ?jq,è _j ?R,è0=1 *

et è q ?R avec ( )

å _t i . i . d 0, ó _å .

2

Processus AR :

Le processus (X_t, t ? Z) satisfait une représentation AR d'ordre P, notée AR(p), si et seulement si :

Ö (L)X t = m+ å t

p

avec E (Xt) = m. et c? R ,le polynôme étant défini par : ( ) Ö L

= èL j

j

j 0

où ?jp,è _j ?R,è0=1 *

et è p ? R , avec ( )

å _t i . i . d 0, ó _å .

2

1.1.b. Processus Aléatoires non stationnaires :

La plupart des séries économiques sont non stationnaires, c'est -à- dire que le processus qui les décrit ne vérifie pas au moins une des conditions de la définition d'un processus stationnaire du second ordre. Le fait qu'un processus soit stationnaire ou non conditionne le choix de la modélisation que l'on doit adopter. Par exemple, si l'on s'en tient notamment à la méthodologie de Box et Jenkins, et si la série étudiée est issue d'un processus stationnaire, on cherche alors le meilleur modèle parmi la classe des processus stationnaires pour la représenter, puis on estime ce modèle. En revanche, si la série est issue d'un processus non stationnaire, on doit avant toutes choses, chercher à la »stationnariser», c'est à dire à trouver une transformation stationnaire de ce processus. Puis, on modélise et on estime les paramètres associés à la composante stationnaire.

Pour détecter la non stationnarité, on utilise en premier lieu la méthode graphique pour avoir une idée sur le type de non stationnarité, et par suite on utilise la méthode analytique.

Méthode graphique :

Analyse du graphe de la série :

· Si le modèle est avec rupture, la série présente une rupture de moyenne à partir d'une certaine date.

· Si la moyenne du processus qui génère la série évolue avec le temps, la non stationnarité est de type déterministe.

· L'étude des graphes représentant l'évolution de la moyenne, ainsi que celui de la variance peut aider à détecter une éventuelle non stationnarité.

Analyse du corrélogramme :

· L'étude du corrélogramme, nous permet de détecter une non stationnarité.

· La décroissance de manière non exponentielle de la fonction d'autocorrélation, nous indique une non stationnarité de la série. (le corrélogramme d'un processus stationnaire présente une décroissance «rapide»)

Toutefois, si ces représentations graphiques peuvent (dans certains cas) nous indiquer qu'une série est non stationnaire, elles ne nous permettent pas de déterminer le type de non stationnarité c'est pourquoi il faut recourir par la suite à la méthode analytique.

Il existe différentes sources de non stationnarité et à chaque origine de la non stationnarité est associée une méthode propre de stationnarisation. Selon la terminologie de Nelson et Plosser (1982) il y'a deux classes de processus non stationnaires : les processus TS (Trend Stationary) et les processus DS (Differency Stationary).

1. Processus TS :

Cette forme de non stationnarité provient de la présence d'une composante déterministe tendancielle. Définition: (X_t, t? Z) est un processus TS s'il peut s'écrire sous la forme X t = f (t) +z t

où f (t) est une fonction du temps et z _t est un processus stochastique stationnaire.

le processus X _t s'écrit comme la somme d'une fonction déterministe du temps et d'une composante

stochastique stationnaire. Ce processus ne satisfait plus la définition de la stationnarité du second ordre. On a en effet :

E (X_t) = f (t) + E(z _t )

Une des propriétés importantes de ce type de processus réside dans l'influence des innovations stochastiqueså _t . Lorsque un processus TS est affecté par un choc stochastique, l'effet de ce choc tend à

disparaître au fur et à mesure que le temps passe : C'est la propriété de non persistance des chocs.

Pour stationnariser un processus TS, il convient de retirer la composante déterministe f(t) en régressant la série X _t sur la plan défini par les puissances de t.

2. Processus DS: Cette forme de non stationnarité est de nature stochastique.

Définition:

Un processus non stationnaire (X_t, t? Z) est un processus DS (Differency Stationnary) d'ordre d, où d

désigne l'ordre d'intégration, si le processus filtré défini par d

(1 - L) X _t est stationnaire. On dit aussi

que (X_t, t ?Z) est un processus intégré d'ordre d, noté I (d).

- Ainsi, on peut définir une classe de processus stochastiques qui ne satisferont pas les conditions de la stationnarité, mais dont la différence à l'ordre d satisfait elle les propriétés de la stationnarité.

-la définition des processus DS repose sur la présence de racines unitaires dans le polynôme associé à la dynamique autorégressive du processus.

Dans la classe générale des processus DS, un type de processus apparaît de façon régulière, si bien que l'on lui a attribué un nom particulier : la marche aléatoire.

Définition : Une marche aléatoire (Random Walk), ou martingale, est un processus AR(1) intégré d'ordre un, noté I (1) :

ÄX t = (1 - L) X t = c + å t ? X t = c + X _t-1 + å t

où å _t est un bruit blanc i.i.d. ( )

0, ó_å . Si c = 0, on parle d'une marche aléatoire pure (Pure Random

2

Walk).

Pour stationnariser un processus DS d'ordre d, il convient d'appliquer le filtre d

(1 - L) .

Propriétés des processus DS :

1. Un processus non stationnaire (X_t, t? Z) est un processus DS intégré d'ordre d, noté I (d), si

le polynôme ö (L) défini en l'opérateur retard L, associé à sa composante autorégressive admet

d racines unitaires :

ö(L) X t = Z _t avec ö (L) = (1 - L) ö^? (L)

d

où Zt est un processus stationnaire, et si les racines du polynôme ö (L)	sont toutes strictement

supérieures à l'unité en module.

2. L'influence d'une innovation å _t à une date T sur un processus I (d) : d

(1 - L) X t = è (L) å t

est permanente. On a ainsi une propriété de persistance des chocs.

Conséquences d'une mauvaise stationnarisation du processus :

· La différenciation d'un processus TS conduit à une autocorrélation fallacieuse du résidu du filtre.

· L'extraction d'une tendance linéaire d'un processus DS conduit à créer artificiellement une forte autocorrélation des résidus aux premiers retards.

3. Tests de Racine Unitaire:

Ces tests permettent, tout d'abord de vérifier que les séries sont non stationnaires, et d'autre part de discriminer entre les processus DS et TS.

Le Test de Dickey Fuller simple (DF) :

Le test de Dickey Fuller simple (1979) est un test de racine unitaire (ou de non stationnarité) dont l'hypothèse nulle est la non stationnarité d'un processus autorégressif d'ordre un. Considérons un processus (X_t, t ?Z) satisfaisant la représentation AR(1) suivante :

X t = ñ X _t-1 + å t avec ( ² )

å _ti . i . d 0, ó _å ,et ñ ?R .

Le principe général du test de Dickey Fuller consiste à tester l'hypothèse nulle de la présence d'une racine unitaire :

H : = 1

ñ

0

H : || < 1

ñ

1

La distribution asymptotique de l'estimateurñà obtenue sous H₀ est non standard (non normale), et en particulier non symétrique.

La distribution asymptotique, sous H₀, de la statistique de Student t ñ à = 1 du test de Dickey-Fuller n'est
pas standard. On a :

1

2 x t 2 - 1 1

N

ñ à 1

= 2

=

= - = -

( ) ( )

ñ ñ

t

à 1 à 1 t

ó S

ñ

à N

N N

et 2 = = -

( ) ( ) ( )2

1 1

å ñ -

2

S à à

N X X 1

- -

1 1

t t t

N N

t = 1 t = 1

Sous l'hypothèse H₀ de non stationnarité, la distribution asymptotique de la statistique de Student t ñ à = 1 diffère suivant que le modèle utilisé soit sans constante, ou avec constatnte, ou bien avec constate et trend.

Le test de l'hypothèse ñ = 1 est identique au test de l'hypothèse ö = 0 dans le modèle transformé suivant:

ÄX t = öX _t-1 + å t

Avec ö = ñ-1 et t

Ä X = (1 - L)X t = X _t - X t -1, et le test de Dickey-Fuller se ramène alors à : H : = 0

ö

0

H : < 0

ö

1

La statistique à = 0

t _ö a la même distribution asymptotique quet ñ à = ₁, et il faux utiliser les seuils critiques tabulés par Dicke-Fuller (1979) ou Mc Kinnon (1981) pour effectuer les test de non stationnarité. Stratégie du Tests:

Une stratégie de tests de Dickey Fuller permet de tester la non stationnarité conditionnellement à la spécification du modèle utilisé. On considère trois modèles définis comme suit :

Ä X t = öXt-1 + å_t modèle 1;

Ä X t = ö X _t-1 + c + å t modèle 2;

ÄX t = öX _t-1+ c + â t + å t modèle 3.

Déroulent de la stratégie du test DF :

On commence par tester la racine unitaire à partir du modèle 3.Si la réalisation de à = 0

t _ö est

supérieure au seuil ³

C_á tabulé par Dickey et Fuller, pour le modèle 3, on accepte l'hypothèse nulle de

nonstationnarité. Par la suite on cherche à vérifier si la spécification du modèle 3, était une spécification compatible avec les données. On teste alors la nullité du coefficient â de la tendance. Deux cas sont envisageables:

· Soit on a rejeté au préalable l'hypothèse de racine unitaire, dans ce cas on teste la nullité de â par un test de Student avec des seuils standards (test symétrique, donc seuil de 1.96 à 5%), si l'on rejette l'hypothèse â = 0, cela signifie que le modèle 3 est le »bon» modèle pour tester la racine unitaire, la série est TS. En revanche, si l'on accepte l'hypothèse â = 0, on doit refaire le test de racine unitaire à partir du modèle 2.

· Soit, on avait au préalable, accepté l'hypothèse de racine unitaire, et dans ce cas, on doit construire un test de Fischer de l'hypothèse jointeö = 0 et â = 0.

On teste ainsi la nullité de la tendance, conditionnellement à la présence d'une racine unitaire: H : (c; â; ö) = (c; 0; 0) contre H 1

3 3

0

La statistique de ce test se construit par la relation :

2

F 3 =

( )

SCR _C SCR

-

3, 3

3

SCR

( )

N K

-

SCR3 ,C : somme des carrés des résidus du modèle 3 contraint sous 3

H₀ (ÄX t = c + å _t ).

SCR₃ : somme des carrés des résidus du modèle 3 non contraint.

N : nombre d'observations.

K : nombre de coefficients à estimer.

y' Si la réalisation de F₃ est supérieure à la valeur ö₃ lue dans la table à un seuil á %, on rejette l'hypothèse 3

H₀ .Dans ce cas, le modèle 3 est le »bon», et la sérieX _t est intégrée d'ordre 1

(I(1)+T+c).

y' Si on accepte ³

H₀ , le coefficient de la tendance est significativement nul, conditionnellement à la présence d'une racine unité, le modèle 3 n'est pas le »bon» modèle, on doit effectuer à nouveau le test de non stationnarité dans le modèle 2.

Si l'on a accepté la nullité du coefficient â de la tendance, on doit alors effectuer à nouveau les tests de non stationnarité à partir cette fois-ci du modèle 2. Si la réalisation de à = 0

t _ö est supérieure au seuil ²

C_á tabulé par Dickey et Fuller, pour le modèle 2, on accepte l'hypothèse nulle de non stationnarité. Par la suite on cherche à vérifier si la spécification du modèle 2, était une spécification compatible avec les données. On teste alors la nullité du coefficient C de la constante. Deux cas sont envisageables:

· Soit on a rejeté au préalable l'hypothèse de racine unitaire, dans ce cas on teste la nullité de C par un test de Student avec des seuils standards (test symétrique, donc seuil de 1.96 à 5%). Si l'on rejette l'hypothèse C = 0, cela signifie que le modèle 2 est le »bon» modèle pour tester la racine unitaire. La série est stationnaire. En revanche, si l'on accepte l'hypothèse C = 0. On doit refaire le test de racine unitaire à partir du modèle 1.

· Soit, on avait au préalable, accepté l'hypothèse de racine unitaire, et dans ce cas, on doit construire un test de Fischer de l'hypothèse jointeö = 0 et C = 0.

On teste ainsi la nullité de la constante, conditionnellement à la présence d'une racine unitaire:

H : (c; ö ) = (c;0) contre H 1

2 2

0

La statistique de ce test se construit par la relation :

( )

SCR _C SCR

-

2, 2

( )

N K

-

F₂ =

2

2

SCR

SCR2,C : somme des carrés des résidus du modèle 2 contraint sous 2

H₀ (ÄX t = å _t ).

SCR₂ : somme des carrés des résidus du modèle 2 non contraint.

N : nombre d'observations.

K : nombre de coefficients à estimer.

y' Si la réalisation de F₂ est supérieure à la valeur ö₂ lue dans la table à un seuil á%, on rejette l'hypothèse ²

H₀ . Dans ce cas, le modèle 2 est le »bon» modèle et la série X _t est intégrée d'ordre 1 (I(1)+C).

y' Si on accepte ²

H₀ , le coefficient de la constante est nul, le modèle 2 n'est pas le »bon» modèle, on doit donc effectuer à nouveau le test de non stationnarité dans le modèle.

Si l'on a accepté la nullité du coefficient C de la constante, on doit alors effectuer à nouveau les tests de non stationnarité à partir cette fois-ci du modèle 1.

y' Si la réalisation de à = 0

t _ö est supérieure au seuil ¹

C_á tabulé par Dickey et Fuller, pour le modèle 1, on accepte l'hypothèse nulle de non stationnarité, la série est intégrée d'ordre1 I (1). (pure marche aléatoire).

y' Si la réalisation de à = 0

t _ö est inférieure au seuil ¹

C_á tabulé par Dickey et Fuller, pour le modèle 1,

on refuse l'hypothèse nulle de non stationnarité, la série est stationnaire I (0).

Le Test de Dickey Fuller Augmenté (ADF):

Il est nécessaire de tester la non stationnarité de la série en prenant en compte l'autocorrélation des perturbationså_t . C'est précisément l'objet des tests de Dickey Fuller Augmentés (ou ADF). Les trois modèles utilisés pour développer le test ADF sont les suivants :

p

Ä = +

X Ä + modèle1;

t 1

ö X - î X - å t j t j t
j 1

p

Ä = +

X Ä + + modèle2;

t 1

ö X - î X - c å t j t j t
j 1

p

Ä = +

X Ä + + + modèle3.

t 1

ö X - î X c â t å

t j t j t

-

j

1

Déroulent de la stratégie du test ADF :

· Déterminer le nombre de retard p nécessaire pour blanchir les résidus.

· Appliquer la stratégie du test de Dickey Fuller Simple aux modèles, 1,2 et 3. Les distributions asymptotiques des statistiques de test _töà obtenues dans ces trois modèles sont identiques à celles

obtenues dans les modèles de Dickey Fuller Simple correspondants. 4. Choix du nombre de retards optimal :

Critères d'information :

Pour un modèle avec p retard, ayant comme somme des carrées des résidusSCR _P obtenu avec N

observations.

Le critère d'Akaike, ou AIC, est défini par :

AIC p N N

( ) 2

= log SCR P P

+

Le critère de Schwarz, ou SC, est défini par:

SC p N N

( ) log

= log SCR P P N

+

On retient comme p celui qui minimise ces deux critères. Principe de parcimonie:

Lorsque l`on désir modéliser une série chronologique, par un processus stochastique, on doit chercher à minimiser le nombre de paramètres requis, tout en expliquant le mieux possible le comportement de la série.

5. Estimation des paramètres: Une fois le nombre de retards optimal déterminé, on estime les paramètres du modèle retenu par la

méthode des moindres carrée.

Test concernant les paramètres :

Une fois les paramètres estimés, il faut vérifier que les paramètres estimés sont bien

significativement différents de zéro. Pour cela on utilise : Le test de Student : t obs = bjóà bj

b_j: f^i' Coefficient du modèle.

er_b : écart type du f^i' Coefficient du modèle.

j

Si la statistique _tobs est supérieure à 1.96(quantile d'ordre (1- á) de la loi normale),le coefficient est approximativement significatif au niveau de risque de 5%.

6. Analyse du résidu : Pour un ordre h Le test de Box-Pierce permet d'identifier les processus bruit blanc .le test s'écrit :

H0 : ñ₁ = ñ₂ = ñ₃ = = ñh = 0 Contre H₁ : ?j ? [1, h]tq : ñ_h = 0

Pour effectuer ce test, on utilise la statistique de Box et Pierce (1970) Q, donnée par:

h

Q_h =NE 7,2

k'k

k 1

- N : nombre d'observation.

- h : pris généralement égal à N/4.

- ñà_h : autocorrélation empirique d'ordre h.

Asymptotiquement, sous H₀ , Q_h suit un ²

÷ à h degrés de liberté. Nous rejetons l'hypothèse de bruit blanc au seuil h si Q est supérieure au quantile d'ordre (1-á) de la loi du 2^,2 à h degrés de liberté.

Une statistique ayant de meilleures propriétés asymptotiques peut être utilisée celle de Ljung -Box:

2

Q' _h=N (N +2)Y ñk

-K

Asymptotiquement, sous H₀, Q^'_h suit un ²÷ à h degrés de liberté. Nous rejetons l'hypothèse de bruit blanc au seuil h si Q est supérieure au quantile d'ordre (1-á) de la loi du 2^,2 à h degrés de liberté.

h

1.2. Modélisation Multivariée et Cointégration:

Un modèle VAR(vector autoregressive) est un outil économétrique particulièrement adapté pour mesurer et utiliser en simulation, l'ensemble des liaisons dynamiques à l'intérieur d'un groupe de variables donnés. Toutes les variables sont initialement considérées comme étant potentiellement endogènes. C'est-à-dire chaque variable est expliquée par chacune des autres variables, et par sa propre évolution, mais est simultanément variable explicative d'une ou de plusieurs autre variables du modèle.

En règle général, la modélisation VAR consiste à modéliser un vecteur de variables stationnaires à partir de sa propre histoire et chaque variable et donc expliquée par le passé des autres variables.

1.2.a. Modélisation VAR :

1. Représentation générale d'un modèle VAR:

Définition:

Un processus vectoriel {X_t , t ? Z}, de dimension (k, 1) , admet une représentation VAR d'ordre p,

notée VAR(p) si :

X = c + Ö X + Ö X + + Ö _p X _t-p + å_t

t 1 t-1 2 t-2

ou de façon équivalente :

Ö (L)X t = c + å t

P

où c de dimension (k, 1) désigne un vecteur de constantes,( ) 2

Ö L = I ? Ö L ? Ö L - ??? ? Ö _P L n 1 2

où les matrice Ö _i ,i ? [0,p] de dimension (k, k), satisferont Ö 0 = I_k etÖ _P ?0_k .Le vecteur (k,1) des

Ö Ö Ö

i i i

? ?

innovations å_t est i.i.d. (0_k, Ù ) où Ù est une matrice (k, k) symétrique définie positive. On pose les définitions suivantes:

1,1 1,2 1, k

t

x1,

x 2, t

?

X_t

å_t

x k t

,

1 ,

å t Ö Ö Ö

i i i

? ?

2,1 2,2 2, k

å 2, t

? Ö = ? ? ? ?

Ö ? ?

ⁱ . 1,

i p

[ ]

i j , f

å k t

, Ö Ö Ö

i i i

? ?

k k

,1 ,2 k k

,

? ? ? ? ?

Le processus vectoriel des innovations { å _t , t ?Z } est i. i.d. (0_k , Ù ) , et satisfait par conséquent les propriétés suivantes :

Ù =

E, ( )
å å - = t t j

j 0

0 0

j ?

E ( å _t ) = 0 et

Conditions de stationnarité :

La définition de la stationnarité d'ordre deux (ou stationnarité du second ordre) est identique à celle du cas des processus univariés.

Définition:

Un processus vectoriel {X_t , t ? Z}, de dimension (k, 1) , est dit stationnaire au second ordre, ou

stationnaire au sens faible, si:

1. E(X _t )=m,?t?Z.

2. V(X t ) 8 ,?t?Z.

3. ( ) ( )( ) ( ) 2

COV X _t X t + h E X _t m X t h m ( h ), t , h .

, = - + - = ? ? Z

Propositions:

1.Un processus vectoriel {X_t , t ? Z}, de dimension (k, 1) , est stationnaire si et seulement si les racines

du déterminant du polynôme matricielÖ(L), notéeë _i i? [1, k], sont toutes supérieures à l'unité en

module.

2.Un processus vectoriel {X_t , t ? Z}, de dimension (k, 1) , est stationnaire si et seulement si les valeurs

propres de l'application linéaire Ö (L), notéesë ? _i,i ? [1, k], sont toutes inférieures à l'unité en module.

3. Tout processus {X_t , t ? Z}, de dimension (k, 1), stationnaire, satisfaisant une représentation VAR(p), admet une représentation moyenne mobile VMA (8) définie par :

8

X = + = + Ø ( )

t i t i

ì ø å ì L å

- t

i = 0

8

avec -1

ì = E (X _t ) = Ö (1) c.

Le polynôme matriciel ( ) Ø L

=øL i

i

satisfait la relation de récurrence suivante :

i = 0

ø 0 = I_k

ø ø - ø - p ø S p s

S 1 S 1 2 S 2 , 1

= Ö + Ö + ??? + Ö - ? = avec ø_S =0 ?S0 .

2. Estimation d'un modèle VAR:

Les paramètres du modèle VAR ne peuvent être estimés que sur des séries chronologiques stationnaires. Le modèle peut être estimé en appliquant la méthode des moindres carrés ordinaires(MCO), sur chaque équation séparément, ou on peut appliquer également la méthode du maximum de vraisemblance.

Le nombre de paramètres à estimer pour un modelé VAR avec k variables et p décalages est égale à pk ou 2

² pk+ k en prenant les termes constants contenus dans le vecteur C.

Soit le modèle VAR(p) estimé :

X = à c + Ö à X + Ö à X + + Ö à X + e_t

t 1 t-1 2 t-2 p t-p

e_t : vecteur des résidus d'estimation de dimension (k,1) , ( )

e t = e 1, t , e 2, t , , e k , t .

3. Détermination du nombre de retards p:

On peut déterminer le nombre de décalage p en utilisant les critères d'information. En pratique, il suffit de déterminer "à priori" un nombre de décalage maximal p_Max et d'estimer successivement les

modèles VAR(p) pourp = 1, _,pMax .pour chaque modèle estimé la valeur du critère d'information est

calculée. Et le retard p retenu est celui qui minimise ce critère pour p = 1, , p _Max .

Le critère d'Akaike, ou AIC, est défini par :

AIC p N

( ) ( ) 2

2

= Ù +

log à K P

Le critère de Schwarz, ou SC, est défini par:

( ) ( ) ² log

N

= Ù +

log à K P N

SC p

Ù^à: matrice de variance covariance des résidus estimés du modèle, K : nombre de variables du modèle,

N : nombre d'observations.

4. Dynamique d'un modèle VAR:

Les modèles VAR permettent d'analyser les effets de la politique économique, cela à travers de l'analyse de chocs aléatoires (innovations) et de la décomposition de la variance de l'erreur. Cependant, cette analyse s'effectue, en supposant l'invariabilité de l'environnement économique.

Analyse des chocs :

On considère un processus {X_t , t ? Z}, avec '

X t = (x1, t , ... , x k, t ) satisfaisant une représentation VAR (p). On suppose que les innovations { å _t , t ?Z} sont i.i.d. (0_k, Ù ) .et que l'on dispose de T + p réalisations de ce processus, on suppose en outre que les paramètres Ù , Ö _i sont connus, mais la même analyse peut être menée lorsque l'on ne dispose que d'estimateurs convergents de ces paramètres.

Idée Générale: Une fonction de réponse aux innovations résume l'information concernant l'évolution d'une composante xi , t qui intervient suite à une impulsion sur xj , t à la date T, en supposant que toutes les autres variables sont constantes pour t = T.

Pour expliciter les choses, on considère le VAR(1) suivant :

x

x c x x

Ö + Ö

¹

t t t t

= + + å

- -

, 1 1,1 1, 1 1,2 2, 1 1,

= + Ö + Ö +

c x x å

2, 2 2,1 1, 1 2,2 2, 1 2,

t t t t

- -

Avec ( )'

X t = x _1,t , x _2,t et( )'

å t = å 1, t , å 2 , t .

On suppose que les chocs å 1 , t et å 2 , t sont corrélés, avec : ( ) E t t å å '

ó ó 2 1 12 = = Ù ó ó ^2 12 2

On cherche à identifier l'impact d'un choc sur x2 , T à la date T sur la dynamique de la variable x _1,t aux périodes postérieures à T, en supposant les évolutions de ces deux variables pour t = T connues et données.

On cherche donc à déterminer la variation de x_1,t engendrée par ce choc. Pour cela, considérons la décomposition suivante :

8

x i t

= +

ì ø å

1 ,t 1 1 ,

i =0

Où ø_1,i désigne la première ligne de la matrice Ø _i issue de la représentation VMA( 8).

En raison de la corrélation des deux chocs, l'impulsion initiale sur å _2,T influence l'innovation å _1,T qui entre elle aussi dans la représentation moyenne mobile infinie de x 1 , t . Or ,Ce qui est intéressant sur le plan économique, c'est d'isoler l'innovation »propre» au processus x 2 ,t . non »polluée» par la réaction de l'innovation x 1 , t . C'est pourquoi, il convient dans le cas général où Ù ? I_K d'orthogonaliser les innovations.

On considère donc la décomposition suivante de la matrice de covariance des innovations:( )'

Ù = P P

-1 -1

où 1

P- est une matrice (k, k) triangulaire inférieure.

Dans notre exemple:

ó12

2 1 1

ó ó

0

( ) P ^-1

'

ó ó ó

1 12 1 -1

Ù= = 2

ó ó ó

2 2

ó ó = P

12 12 2

ó

12 2 2 2

-

ó ó ó

2 12

0 -

1 1 2 2

ó 1

On pose : -1

í t = På _t (ce qui garanti que ces innovations ne sont pas corrélées).

Si on pose å t = Aí _t la représentation VMA (8) peut se réécrire en fonction des innovations í_t non corrélées. De façon équivalente, on peut réécrire le V AR en fonction des innovations orthogonales :

x 1, t = c₁ +Ö _1,1 x 1, t - 1 + Ö _1,2 x _2,t-1 + ó ₁ í 1 , t

ó ó ²

x c x x t

t = + Ö t - + Ö t - + t + -

12 2 12

í ó í

( )

2, 2 2,1 1, 1 2,2 2, 1 1, 2 2 2,

ó ó

1 1

Cette phase d'orthogonalisation implique toutefois que l'ordre dans lequel sont disposées les variables du VAR affecte l'analyse dynamique et en particulier l'analyse des fonctions de réponse.

Les fonctions de réponses sont souvent représentées sous la forme d'un tracé permettant de visualiser simplement les effets instantanées et dynamiques associées aux chocs d'innovations sur les variables du vecteurX _t .

Décomposition de la variance:

Définition: Partant de la décomposition des résidus en innovations »pures» ou orthogonales, on peut calculer quelle est la contribution de chaque innovation à la variance totale de l'erreur de prévisions du processus x _i,t . C'est ce que l'on appelle la décomposition de la variance.

On considère un processus {X_t , t ? Z}, avec '

X t = (x1, t , ..., x k, t ) satisfaisant une représentation VAR (p). On suppose que les innovations { å _t , t ?Z} sont i. i.d. (0_k, Ù ) . On suppose que ce processus est stationnaire et peut être représenté sous la forme d'un VMA(8) :

8

X ø å L å

= = Ø

t i t i t

( )

-

i=0

L'erreur de prévision à l'horizon h s'écrit :

X - à X = X - E (X /X ,X , . . . ,X )

T+h T+h T+h T+h T T-1 1

= X_T+h - E _(XT+h/ å _T, å _T-1, ..., å ₁ )

.

h - 1

= ø å

i T h i

+ -

i = 0

La matrice de variance covariance de l'erreur de prévision est donc :

( ) ( ) 1

h -

' ø ø '

E X - X à X - X à = Ù + Ù .

T+h T+h T+h T+h i i

i = 1

En considérant : í t = På t å t í t 1 ? = P -

où la matrice 1 P- est issue de l'orthogonalisation de ~ : ( )' Ù = P P . -1 -1

On suppose que ?t ? Z:

å í

1, t 1, t

å í

2, 2,

å = =

t t

t 1 2

( ) ? Où a_i désigne la i^ème colonne de la matrice 1

P- ? i ? [ 1,k ] . Dès

a a a

? k

?

å í

k t

, k t

,

lors:

Ù = E ( å _t å _t ) = a1a ₁ V _(v1,t ) + a2a ₂ V _(v2,t )+ +aka _k V (vk,t).

' ' ' '

En substituant cette expression dans la variance de la prévision pour un horizon h, cela donc permet de réexprimer cette variance en fonction de la variance des innovations »orthogonales» :

k h - 1

'

EX - X à X - X à

( ) ( ) ( ) ( )

V í ø a a ø

' '

=

T +h T +h T + h T +h j t i j j i

,

j = =

1 1

i

A partir de cette formule, on est en mesure de calculer la contribution d'une innovation pure íj _,t à la variance totale de la prévision à un horizon h :

V í ø a a ø + ø a a ø + + ø _k a _j a _j ø k

( ) { ( ) ( ) ( )

' ' ' ' ' ' }

j , t 1 j j 1 2 j j 2

La Causalité:

Une des questions que l'on peut se poser à partir d'un VAR, est de savoir s'il existe une relation de causalité entre les différentes variables du système.

Causalité au sens de Granger:

Définition :

On dit que la variable x cause au sens de Granger la variable y si et seulement si la connaissance du passé de x améliore la prévision de y à tout horizon.

Considérant le VAR(p) suivant avec k=2 avec x _t et y _t stationnaires :

x x

c x x

1 1 2 ² Ö Ö

p ^p å

t t p

1 1,1 1,2 1,1 1,2 2

Ö Ö t - -

Ö Ö

1 t - 1,1 1,2 t

= + + + ????? + +

y y

1 1 2 ² Ö Ö

p p

t t p

c y y

2 2,1 2, 2 2,1 2,2 2

Ö Ö í

t - -

Ö Ö

1 t - 2,1 2,2 t

Un test d'hypothèses jointes permet de conclure sur le sens de la causalité. Ainsi, x _t cause y _t au sens de Granger si l'hypothèse nulle définie ci-dessous peut être rejetée au profit de l'hypothèse alternative:

De façon analogue, y _t cause x _t au sens de Granger si l'hypothèse nulle définie ci-dessous peut être rejetée au profit de l'hypothèse alternative :

H 0 : 1,2 1,2 p 1,2

Ö = Ö = ?? = Ö

1 2

H₁ : Au mois un des _1,2 0 [ 1, ]

Ö i ? ? i ? p .

Les tests peuvent être conduites en utilisant les tests portant plusieurs paramètres à la fois (test de Wald) Par ailleurs, si l'on est amené à rejeter les deux hypothèses nulles, on a une causalité bidirectionnelle, on parle de boucle rétroactive (feedback effect).

1.2.b. Cointegration :

Rappelons la définition d'un porcessus intégré :

Définition :

Un processus (X_t, t? Z) est un processus DS (Differency Stationnary) d'ordre d, ou un processus intégré d'ordre d, si le processus filtré défini par d

(1 - L) X _t est stationnaire.Partant de là, on peut

introduire la notion de cointégration :

Définition :

On considère un processus vectoriel '

X t = (x _1,t x _2,t ...x _N,t ) de dimension (N, 1) intégré d'ordre d. Les processus _(xi,t , t ?Z) sont dits cointégrés si et seulement si il existe un vecteur

á = (á₁ á₂ .. .á_N) ?Rtel que la combinaison linéaire '

^N áX _t est stationnaire ou intégré d'ordre 0. Le

vecteurá correspond à un vecteur de cointégration.

Test du nombre de relation de cointégration (Test de la trace):

Le test de Johansen (1988) est fondé sur l'estimation de :

Ä X t = ₀ + 1ÄX _t-1 + 2ÄX _t-2 + ... + p-1ÄX t-p+1 + Ð X _t-1 + å t

i Où 0=C et [ ] = Ö ? ? ? I, j 1,i i j j 1 =

p , et la matrice Ö - I = áâ de dimension r × k . ' Ð = m m=1

r étant alors le nombre de relations de cointégrations, k le nombre de variable du modèle VAR, et les colonnes de â Correspondant aux vecteurs de cointégration.

Ce test est fondé sur les vecteurs propres correspondant aux valeurs propres les plus élevées de la

K

matrice Ð. A partir des valeurs de celle ci on construit la statistique : ë (r) N ln(1 ë )

= - -

trace i

i r 1

= +

- N : nombre d'observation, - r : rang de la matrice,

-ë i : ivaleur propre de la matrice Ð ,

éme

- K : nombre de variable du modèle VAR.

Cette statistique suit une loi de probabilité tabulée par Johansen et Juselius (1990). Ce test fonctionne par exclusion d'hypothèses alternatives :

1. Test 0

H : r = 0 contre H₁ : r > 0. Test de l'hypothèse aucune relation de cointégration contre au moins une relation. Sië _trace(0) est supérieur à la valeur lue dans la table au seuil á %, on rejette H₀ , il existe au moins une relation, on passe alors à l'étape suivante, sinon on arrête et r = 0.

2. Test 0

H : r = 1 contre H₁ : r > 1. . Test de l'hypothèse une relation de cointégration contre au moins deux relation. Si ë _trace(1) est supérieure à la valeur lue dans la tableau seuil á %, on rejette H₀ , il existe au moins deux relations, on passe alors à l'étape suivante, sinon on arrête et r = 1.

Et ainsi de suite jusqu'à la dernière étape (si elle est nécessaire) :

Test H0 : 0

H : r = k-1 contre H₁ : r > k-1. Test de l'hypothèse k-1 relation de cointégration contre au moins k-1 relations. Si ë _trace (k-1) est supérieure à la valeur lue dans la table au seuil á %, on rejette H₀ , il existe K relations de cointégration.

Johansen propose cinq spécifications :

1. Pas de tendance déterministe pour X_t , équations de cointégration sans constantes,

2. Pas de tendance déterministe pourX_t , équations de cointégration avec constantes,

3. Tendance déterministe pourX_t , équations de cointégration avec constantes,

4. Tendance déterministe pourX_t , équations de cointégration avec tendances linéaires,

5. Tendance quadratique pourX_t , équations de cointégration avec tendances linéaires.

Section 2: Principaux résultats et interprétation. 2.1. Présentation des données et méthodologie suivie. 2.1.a. Données :

Dans le cadre de ce mémoire, et pour tester la présence d'une relation entre éducation et croissance économique, nous nous proposons de retenir deux types de variables : les variables éducatives et économiques .Ces différentes catégories de variables seront analysées dans le cas de l'Algérie sur la période 1963-2004.

Compte tenu que le capital humain est lié aux efforts d'éducation consentis par un pays, en ce qui concerne les variables éducatives, nous nous proposons de retenir :

- Effectifs scolarisés à tous les niveaux confondus (SCO), ( er éme éme

1 , 2 ,3 Cycle),

- Nombre de bacheliers (BAC),

- Nombre de diplômés du supérieur (SUP),

- Dépenses d'éducation à prix constants (DEP), (dépenses au niveau du ministère de l'éducation national).

On a calculé les dépenses d'éducation à prix constants de la façon suivante:

( ) =

t

DEPprix courants

t ( )

DEPprix constants déflateur du PIB de la date t

Enfin, la variable économique retenue pour mesurer la croissance économique est le Produit intérieur brut à prix constants (PIB).

Nos donnés sont extraites de trois sources nationales : Le Ministère de L'Enseignement Supérieur et de la Recherche Scientifique (MESRS), le Ministère de l'éducation Nationale (MEN), l'Office National des Statistiques (ONS), et une source internationale: la Banque Mondiale (BM).

2.1.b. Méthodologie :

Afin d'étudier les liaisons entre le PIB et les variables éducatives, nous allons utiliser l'approche des vecteurs autorégressifs (VAR). Dans un premier temps, un modèle VAR à quatre variables est estimé pour étudier la relation entre les variables éducatives (jusqu'à l'obtention du baccalauréat) et le PIB. Dans un second temps, un modèle VAR à deux variables est estimé pour étudier la relation entre le nombre de diplômés et le PIB.

Pour que ces modèles autorégressifs donnent des résultats satisfaisants, nous procédons à la stationnarisation des séries chronologiques avant de déterminer l'ordre du VAR. Nous testons également les degrés de signification des résidus, et enfin nous vérifions la stabilité du modèle.

2.2. Application.

2.2.a. Analyse et traitement des séries :

1. Analyse de la série du produit intérieur brut :

Cette série correspond au produit intérieur brut à prix constant (PIB) de 1963 à 2004. Données, Banque Mondial, annuelles, 1963 à 2004, 42 observations.

Evaluation graphique de la non stationnarité : Série brut :

Figure 1: graphique de la série PIB.

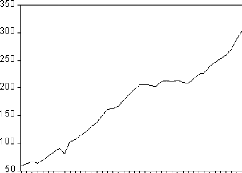
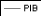
Le graphique de la série du produit intérieur brut fait ressortir une tendance globale à la hausse. Il semble donc que la série soit non stationnaire.

Série transformée :

Afin de stabiliser la série, on lui applique une transformation logarithmique.

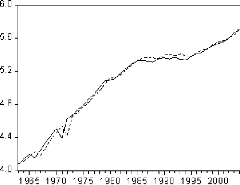
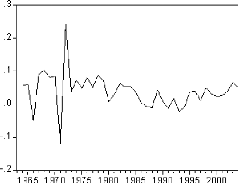
Figure 2: graphique de la série LPIB

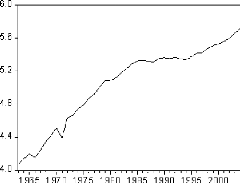
De même, Le graphique de la série logarithme fait ressortir une tendance globale à la hausse. Il semble donc que la série soit non stationnaire. Néanmoins, cette transformation nous assure une première différence plus stable.

Analyse des autocorrélations et autocorrélations partielles:

Figure 3 : corrélogramme de la série LPIB.

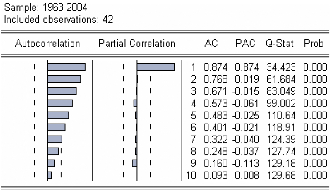
Le premier graphique (corrélogramme) représente les autocorrélations d'ordre h=1,... ,10 , et le
deuxième (corrélogramme partiel) les autocorrélations partielles d'ordre h=1,...,10 . Les colonnes AC

et PAC reportent les valeurs numériques correspondantes. Q-Stat est la valeur de la statistique de LjungBox et Prob la p-value associée.

On remarque que jusqu'au retard h=7 les termes du corrélogramme sont à l'extérieur de l'intervalle de confiance (représentées par des traits pointillés horizontaux).

On constate aussi que toutes les autocorrélations sont significativement différentes de 0 (Prob pour
h=1,... ,10 inférieurs au seuil de 5%) et décroissent très lentement. Ceci est aussi caractéristique d'une

série non stationnaire.

Le test Augmented Dickey Fuller (ADF): Choix du nombre de retards optimal P :

Dans Eviews 5.0, la spécification qui minimise les critères d'information Akaike (AIC) et Schwarz(SC), est faite automatiquement dans le cadre de la procédure de test de racine unitaire. Compte tenu du nombre d'observations disponibles on choisis p_Max =5.

	Modéle1	Modéle2	Modéle3
AIC	0	1	1
SC	0	1	1

Selon le principe de parcimonie, On retient donc p=0 retard.

Stratégie du test:

1-On teste la racine unitaire dans le modèle3 incluant une constante, et un trend :

ÄLPIB _t =öLPIB t - 1 +c +ât + å t

On teste : H₀: ö = 0 vs H₁: ö < 0

t _ö = - 1.481118 > 3

C_á = -3.50 pour un seuil á = 5% (-3.50 pour 50 observations). Donc pour un

à = 0

niveau de risqueá =5% , on accepte l'hypothèse nul de racine unitaire( ö = 0). comme H₀ est acceptée on teste: ³

( )

-

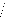
H : (c; â; ö) = (c; 0; 0) contre H 1

3

0

SCR _C SCR 2 0.11236 0.10019 2

-

3, 3 = ( )

F = =2.307

³ SCR N K

( )

- 0.10019 41 3

( )

-

3

Pour une 50 d'observations et un risque de première espèce deá =5% on a: F 3 = 2.307 ö 3 = 6.73.

On accepte ³

H₀ , le modèle 3 n'est pas le »bon» modèle, on doit effectuer à nouveau le test de non

stationnarité dans le modèle 2.

2-On teste la racine unitaire dans le modèle2 incluant une constante :

ÄLPIB _t =öLPIB t - 1 +c + å t

On teste : H₀: ö = 0 vs H₁: ö < 0

t _ö = - 1.932263 > 2

C_á = -2.93 pour un seuil á = 5% (-2.93 pour 50 observations). Donc pour un

à = 0

niveau de risqueá =5% , on accepte l'hypothèse nul de racine unitaire( ö = 0). Comme H₀ est acceptée on teste : 2

H : (c;ö) = (c;0) contre H ₁ .

2

0

Pour une 50 d'observations et un risque de première espèce deá =5% on a: F₂ = 3.73 ö ₂= 5.13. (F₂ dans le test DF simple c'est F-statistic ).

On accepte l'hypothèse ²

H₀ . Dans ce cas, le modèle 2 n'est pas le »bon» modèle, on doit effectuer à nouveau le test de non stationnarité dans le modèle 1.

3-On teste la racine unitaire dans le modèle1 sans constante ni tendance:

ÄLPIB _t =öLPIB t - 1 + å t

On teste : H₀: ö = 0 vs H₁: ö < 0

t _ö = 4.5 1528 > 1

C_á = -1.95 pour un seuil á =5% (-1.95 pour 50 observations). Donc pour un

à = 0

niveau de risqueá =5% , on accepte l'hypothèse nul de racine unitaire( ö = 0). Par conséquent, la série LPIB _t est : I(1).

Vérification de l'ordre d'intégration:

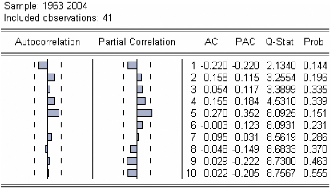
Figure 4 : graphique de la série DLPIB.

D'après le graphique de la série en différence première. Il semble que la série soit stationnaire.

Le test Augmented Dickey Fuller (ADF):

On teste la racine unitaire dans le modèle suivant: 2

Ä LPIB _t =öÄLPIB t - 1 +í t

t _ö = - 5.022624 < 1

C_á = -1.95 pour un seuil á = 5% (-1.95 pour 50 observations). Donc pour un

à = 0

niveau de risqueá =5% , on refuse l'hypothèse nul de racine unitaire( ö = 0). Autrement dit : la série ÄLPIB t = å _test : I(0). (Correspond à un l'innovation å_t ).

Graphiques de la série originale et la série générée:

On compare ici, le graphique de la série originale (LPIB) et la série générée (GLPIB, avec:GLPIB t = LPIB t - 1 +e _t ), pour s'assurer que notre démarche de stationnarisation nous a

donné de bons résultas.

Figure 5: graphiques de LPIB et GLPIB.

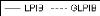
Analyse du résidu :

On analyse le résidu : å t = ÄLPIB t

Figure 6: corrélogramme de l'innovation å_t .

On remarque que pour les retards h=1, ,10 , les termes du corrélogramme sont à l'intérieur de

l'intervalle de confiance (représentées par des traits pointillés horizontaux).

Le test de Ljung -Box nous indique que toutes les autocorrélations sont significativement nulles:

H : ñ = ñ = ñ = = ñ 10 = 0 Contre H 1 : ? j ? [ 1,10 ] tq : ñ j = 0

0 1 2 3

10 2

ñ à

Q N N

' = + =

( )

2 8.7567

k < 2

÷ ₁₀(10) = 18.307 .on accepte H ₀ , en plus (Prob pour

h -

k = 1 N K

h=1, ... ,10 supérieurs au seuil de 5%).Par conséquent, le résidu peut être assimilé à un processus bruit blanc.

En définitive : la série LPIB _t est non stationnaire (I(1)). Dés lors, pour rendre la série

stationnaire, il faut la différencier une fois.

La série SLPIB _t issue de la série LPIB _t est quant à elle stationnaire. On note alors : SLPIB t = ÄLPIB t

2. Analyse de la série des dépenses d'éducation:

Cette série correspond aux dépenses d'éducation à prix constant (DEP) de 1964 à 2004. Données, Ministère de l'éducation nationale, annuelles, 1964 à 2004, 41 observations.

Evaluation graphique de la non stationnarité :

Série brute :

Figure 1: graphique de la série DEP.

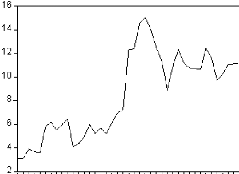
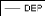
Le graphique de la série brute des dépenses d'éducation fait ressortir une tendance globale à la hausse. Il semble donc que la série soit non stationnaire.

Série transformée :

Afin de stabiliser la série, on lui applique une transformation logarithmique.

Figure 2: graphique de la série LDEP.

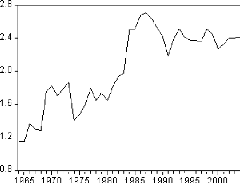
De même, Le graphique de la série logarithme fait ressortir une tendance globale à la hausse. Il semble donc que la série soit non stationnaire. Néanmoins, cette transformation nous assure une première différence plus stable.

Analyse des autocorrélations et autocorrélations partielles:

Figure 3 : corrélogramme de la série LDEP.

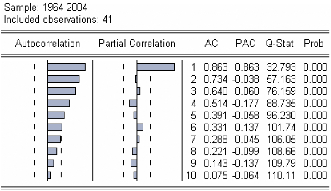
Le premier graphique (corrélogramme) représente les autocorrélations d'ordre h=1,... ,10 , et le
deuxième (corrélogramme partiel) les autocorrélations partielles d'ordre h=1,...,10 . Les colonnes AC
et PAC reportent les valeurs numériques correspondantes. Q-Stat est la valeur de la statistique de Ljung-
Box et Prob la p-value associée.

On remarque que jusqu'au retard h=6 les termes du corrélogramme sont à l'extérieur de l'intervalle de confiance (représentées par des traits pointillés horizontaux).

On constate aussi que toutes les autocorrélations sont significativement différentes de 0 (Prob pour h=1,... ,10 inférieurs au seuil de 5%) et décroissent très lentement. Ceci est aussi caractéristique d'une série non stationnaire.

Le test Augmented Dickey Fuller (ADF):

Choix du nombre de retards optimal P :

Dans Eviews 5.0, la spécification qui minimise les critères d'information Akaike (AIC) et Schwarz(SC), est faite automatiquement dans le cadre de la procédure de test de racine unitaire. Compte tenu du nombre d'observations disponibles on choisis p_Max =4.

	Modéle1	Modéle2	Modéle3
AIC	0	0	0
SC	0	0	0

On retient donc p=0 retard.

Stratégie du test:

1-On teste la racine unitaire dans le modèle3 incluant une constante, et un trend :

ÄLDEP _t =öLDEP t - 1 + c + ât + å _t .

On teste : H₀: ö = 0 vs H₁: ö < 0

t _ö = - 2.120489 > 3

C_á = -3.50 pour un seuil á =5% (-3.50 pour 50 observations). Donc, pour un

à = 0

niveau de risqueá =5% , on accepte l'hypothèse nulle de racine unitaire( ö = 0).

comme H₀ est acceptée on teste: ³

H : (c; â; ö) = (c; 0; 0) contre H 1

3

0

2 = ( )

1.15200 1.00809 2

-

=2.6409

F₃

( )

SCR _C SCR

3, 3

-

SCR N K

( )

- 1.00809 40 3

( )

-

3

Pour 50 observations et un risque de première espèce deá =5% on a: F 3 = 2.64 ö 3 = 6.73 .

On accepte ³

H₀ , le modèle 3 n'est pas le »bon» modèle, on doit effectuer à nouveau le test de non

stationnarité dans le modèle 2.

2-On teste la racine unitaire dans le modèle2 incluant une constante :

ÄLDEP _t =öLDEP t - 1 + c + å t

On teste : H₀: ö = 0 vs H₁: ö < 0

t _ö = - 1.870984 > 2

C_á = -2.93 pour un seuil á = 5% (-2.93 pour 50 observations). Donc pour un

à = 0

niveau de risqueá =5% , on accepte l'hypothèse nul de racine unitaire( ö = 0). 2-comme H₀ est acceptée on teste: ²

H : (c;ö) = (c;0) contre H 1

2

0

Pour 50 observations et un risque de première espèce deá =5% on a: F₂ = 3.50 ö 2 = 5.13. (F₂ dans le test DF simple c'est F-statistic )

On accepte l'hypothèse ²

H₀ . Dans ce cas, le modèle 2 n'est pas le »bon» modèle, on doit effectuer à nouveau le test de non stationnarité dans le modèle 1.

3-On teste la racine unitaire dans le modèle1 sans constante et sans tendance:

ÄLDEP _t =öLDEP t - 1 + å t

On teste : H₀: ö = 0 vs H₁: ö < 0

t _ö = 0.725219> 1

C_á = -1.95 pour un seuil á = 5% (-1.95 pour 50 observations). Donc, pour un

à = 0

niveau de risqueá =5% , on accepte l'hypothèse nul de racine unitaire( ö = 0). Par conséquent, la série LDEP _t est : I(1).

Vérification de l'ordre d'intégration:

Figure 4 : graphique de la série DLDEP.

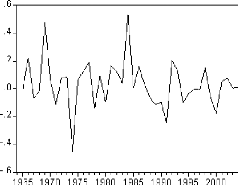
D'après le graphique de la série en différence première, il semble que la série soit stationnaire.

Le test Augmented Dickey Fuller (ADF):

On teste la racine unitaire dans le modèle suivant: 2

Ä LDEP _t =öÄLDEP t - 1 +í t

t _ö = - 6.385222 < 1

C_á = -1.95 pour un seuil á = 5% (-1.95 pour 50 observations). Donc, pour un

à = 0

niveau de risqueá =5% , on refuse l'hypothèse nul de racine unitaire( ö =0) Autrement dit : la série ÄLDEP t = å _test : I(0). (Elle Correspond à l'innovation å_t ) Graphiques de la série originale et la série générée:

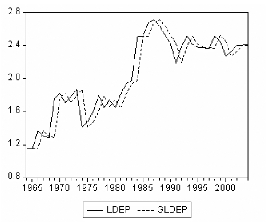
On compare ici, le graphique de la série originale (LDEP) et la série générée (GLDEP, avec: GLDEP t = LDEP t - 1 + e_t), pour s'assurer que notre démarche de stationnarisation nous a donné bons résultas.

Figure 5: graphiques de LDEP et GLDEP.

Analyse du résidu :

On analyse le résidu : å t = ÄLDEP t

Figure 5: corrélogramme de l'innovation å_t .

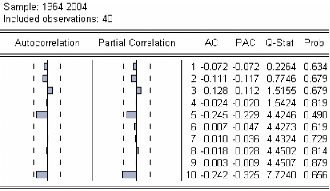
On remarque que pour les retards h=1,... ,10 , les termes du corrélogramme sont à l'intérieur de l'intervalle de confiance (représentées par des traits pointillés horizontaux).

Le test de Ljung -Box nous indique que toutes les autocorrélations sont significativement nulles:

H : ñ = ñ = ñ = = ñ 10 = 0 Contre H 1 : ? j ? [ 1,10 ] tq : ñ j = 0

0 1 2 3

10 2

ñ à

Q N N

' = + =

( )

2 7.7240

k < 2

÷ ₁₀(10) = 18.307 .on accepte H ₀ , en plus (Prob pour

h -

k = 1 N K

h=1, ... ,10 supérieurs au seuil de 5%).Par conséquent, le résidu peut être assimilé à un processus bruit blanc.

En définitive : la série LPDEP _t est non stationnaire (I(1)).Dés lors, pour rendre la série stationnaire, il faut la différencier une fois.

La série SLDEP _t issue de la série LDEP _t est quant à elle est stationnaire. On note : SLDEP t = ÄLDEP t

3. Analyse de la série des effectifs scolarisés à tous les niveaux confondus:

Cette série correspond aux effectifs scolarisés à tous les niveaux (SCO) de 1963 à 2004. Données, Ministère de l'éducation nationale, annuelles, 1963 à 2004, 42 observations,

Evaluation graphique de la non stationnarité :

Série brut :

Figure 1: graphique de la série SCO.

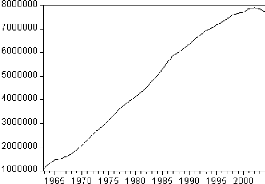
Le graphique de la série des effectifs scolarisés à tous les niveaux fait ressortir une tendance globale à la hausse. Il semble donc que la série soit non stationnaire.

Série transformée :

Afin de stabiliser la série, on lui applique une transformation logarithmique.

Figure 2: graphique de la série LSCO.

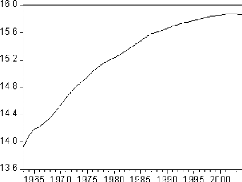
De même, Le graphique de la série logarithme fait ressortir une tendance globale à la hausse. Il semble donc que la série soit non stationnaire. Néanmoins, cette transformation nous assure une première différence plus stable.

Analyse des autocorrélations et autocorrélations partielles:

Figure 3 :corrélogramme de la série LSCO.

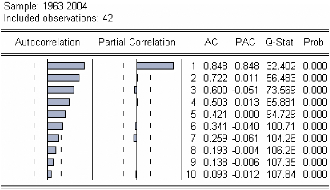
Le premier graphique (corrélogramme) représente les autocorrélations d'ordre h=1,... ,10 , et le
deuxième (corrélogramme partiel) les autocorrélations partielles d'ordre h=1,...,10 . Les colonnes AC

et PAC reportent les valeurs numériques correspondantes. Q-Stat est la valeur de la statistique de LjungBox et Prob la p-value associée.

On remarque que jusqu'au retard h=6 les termes du corrélogramme sont à l'extérieur de l'intervalle de confiance (représentées par des traits pointillés horizontaux).

On constate aussi que toutes les autocorrélations sont significativement différentes de 0 (Prob pour
h=1,... ,10 inférieures au seuil de 5%) et décroissent très lentement. Ceci est aussi caractéristique d'une

série non stationnaire.

Le test Augmented Dickey Fuller (ADF): Choix du nombre de retards optimal P :

Dans Eviews 5.0, la spécification qui minimise les critères d'information Akaike (AIC) et Schwarz(SC), est faite automatiquement dans le cadre de la procédure de test de racine unitaire. Compte tenu du nombre d'observations disponibles on choisis p_Max =4.

	Modéle1	Modéle2	Modéle3
AIC	4	3	3
SC	1	1	3

Selon le principe de parcimonie, on retient donc p=1 retard.

Stratégie du test:

1-On estime le modèle3 incluant une constante, un trend, et un terme différencié retardé:

Ä = ö + + â + î Ä - + å

LSCO LSCO - c t LSCO t t

t 1

t 1

On teste : H₀: ö = 0 vs H₁: ö < 0

t _ö =0.804372 > 3

C_á = -3.50 pour un seuil á =5% (-3.50 pour 50 observations). Donc pour, un

à = 0

niveau de risqueá =5% , on accepte l'hypothèse nul de racine unitaire( ö = 0). 2-comme H₀ est acceptée on teste: 3

H : (c; â; ö) = (c; 0; 0) contre H 1

3

0

F₃

=

2 = ( )

0.00978 0.00666 2

-

=8.439

( )

SCR _C SCR

3, 3

-

SCR N K

( )

- 0.00666 40 4

( )

-

3

Pour une 50 d'observations et un risque de première espèce deá =5% on a: F 3 = 8.43 9 ö 3 = 6.73. On rejette l'hypothèse ³

H₀ , le modèle 3 est le »bon» modèle.

Conclusion:

LSCO _t est I(1)+T+C et ÄLSCO _t est TS . Avec: Ä t = + â + îÄ - 1 + å .

LSCO c t LSCO t t

Vérification de l'ordre d'intégration:

Figure 4 : graphique de la série DLSCO.

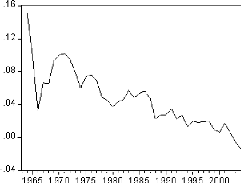
D'après le graphique de la série en différence première, il semble que la série soit affectée d'une tendance déterministe.

Le test Augmented Dickey Fuller (ADF):

On teste la racine unitaire dans le modèle suivant: 2

Ä LSCO = c + â t + îÄ LSCO t - + í t

2

t 1

On teste : H₀: ö = 0 vs H₁: ö < 0

t _ö =-5.259241 < 3

C_á = -3.50 pour un seuil á =5% (-3.50 pour 50 observations). Donc pour un

à = 0

niveau de risqueá = 5% , on refuse l'hypothèse nul de racine unitaire( ö = 0). La différence première n'admet alors pas de racine unitaire.

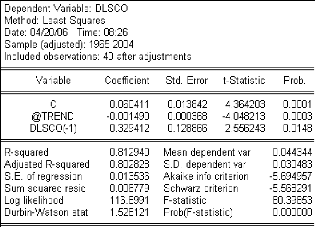
Estimation du modèle :

On estime le modèle suivant : Ä t = + â + îÄ - 1 + å .

LSCO c t LSCO t t

Figure 5 : Estimation du modèle.

-Le coefficient de la tendance est significativement non nul pour un niveau de risqueá =5%,

à

0.001490

ó à 0.000368

â

4.048> 1.96. (Prob inférieure à 5%).

â

tâà = 0

-La constante est significativement non nulle pour un niveau de risqueá =5%,

0.078971

t 4.92 1.96

= = =

à C= 0 ó à C 0.016037

Cà

. (Prob inférieure à 5%).

-Le coefficient î est significativement non nul pour un niveau de risqueá =5%, à

î 0.3294 12 t2.55 1.96

à= 0 = = =

ó à 0.128866

î

î

(Prob inférieure à 5%).

Par conséquent, le modèle en différence première peut être estimé par:

ÄLSCO = 0.06 - 0.001 t + 0.33 LSCO t-1 .

Ä + e_t

t

Graphiques de la série originale et la série générée:

On compare ici, le graphique de la série originale (LSCO) et la série générée (GLSCO,

avec: t t

GLSCO =LSCO+ 0.06 - 0.001 t + 0.33 ÄLSCO _t-1 +e_t .), pour s'assurer que notre démarche de

stationnarisation nous a donné bons résultas.

Figure 5: graphiques de LSCO et GLSCO.

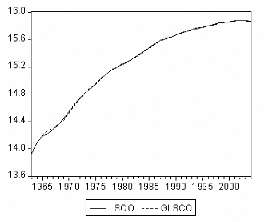
Analyse du corrélogramme des résidus d'estimation:

On analyse le résidu d'estimation å_t du modèle: Ä t = + â + îÄ - 1 + å .

LSCO c t LSCO t t

Figure 6: corrélogramme des résidus d'estimation.

On remarque que pour les retards h=1,... ,10 , les termes du corrélogramme sont à l'intérieur de

l'intervalle de confiance (représentées par des traits pointillés horizontaux).

Le test de Ljung -Box nous indique que toutes les autocorrélations sont significativement nulles:

H : ñ = ñ = ñ = = ñ 10 = 0 Contre H 1 : ? j ? [ 1,10 ] tq : ñ j = 0

0 1 2 3

10 2

ñ à

QN N

' = + =

( )

2 15.487

k < 2

÷ ₁₀(10) = 18.307 .on accepte H₀ , en plus (Prob pour

h -

k = 1 N K

h=1, ... ,10 supérieurs au seuil de 5%).Par conséquent, le résidu peut être assimilé à un processus bruit blanc.

En définitive, la série LSCO _t est non stationnaire de type DS (I(1)+T+C). Dés lors, on considère

la série SLSCO _t stationnaire définie par :

SLSCO = (LSCO -LSCO ) - (0.06 - 0.001 t ) LSCO _t - (0.06 - 0.001 t )

= Ä .

t t t-1

4. Analyse de la série du nombre de bacheliers :

Cette série correspond au nombre de bacheliers (BAC) de 1963 à 2004.

Données, Ministère de l'éducation nationale, annuelles, 1963 à 2004, 42 observations.

Evaluation graphique de la non stationnarité : Série brut :

Figure 1: graphique de la série BAC.

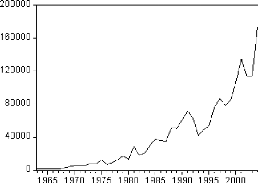
Le graphique de la série du nombre de bacheliers fait ressortir une tendance globale à la hausse. Il semble donc que la série soit non stationnaire.

Série transformée :

Afin de stabiliser la série, on lui applique une transformation logarithmique.

Figure 2: graphique de la série LBAC.

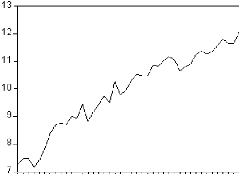
De même, Le graphique de la série logarithme fait ressortir une tendance globale à la hausse. Il semble donc que la série soit non stationnaire. Néanmoins, cette transformation nous assure une première différence plus stable.

Analyse des autocorrélations et autocorrélations partielles:

Figure 3 :corrélogramme de la série LBAC.

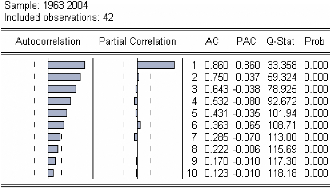
Le premier graphique (corrélogramme) représente les autocorrélations d'ordre h=1,... ,10 , et le
deuxième (corrélogramme partiel) les autocorrélations partielles d'ordre h=1,...,10 . Les colonnes AC

et PAC reportent les valeurs numériques correspondantes. Q-Stat est la valeur de la statistique de LjungBox et Prob la p-value associée.

On remarque que jusqu'au retard h=6 les termes du corrélogramme sont à l'extérieur de l'intervalle de confiance (représentées par des traits pointillés horizontaux).

On constate aussi que toutes les autocorrélations sont significativement différentes de 0 (Prob pour
h=1,... ,10 inférieurs au seuil de 5%) et décroissent très lentement. Ceci est aussi caractéristique d'une

série non stationnaire.

Le test Augmented Dickey Fuller (ADF): Choix du nombre de retards optimal P :

Dans Eviews 5.0, la spécification qui minimise les critères d'information Akaike (AIC) et Schwarz(SC), est faite automatiquement dans le cadre de la procédure de test de racine unitaire. Compte tenu du nombre d'observations disponibles on choisis p_Max =5.

	Modéle1	Modéle2	Modéle3
AIC	1	5	1
SC	1	1	1

Selon le principe de parcimonie, on retient donc p=1 retard.

Stratégie du test:

1-On teste la racine unitaire dans le modèle3 incluant une constante, un trend,et un terme différencié retardé :

ÄLBAC =öLBA C_- + c + â t + î Ä LBAC + å t

t 1

t t -1

On teste : H₀: ö = 0 vs H₁: ö < 0

t _ö = -2.256430 > 3

C_á = -3.50 pour un seuil á =5% (-3.50 pour 50 observations). Donc, pour un

à = 0

niveau de risqueá =5% , on accepte l'hypothèse nul de racine unitaire( ö = 0).

comme H₀ est acceptée on teste: ³

( )

-

H : (c; â; ö) = (c; 0; 0) contre H 1

3

0

SCR _C SCR 2 2.9333 2.5375 2

-

3, 3 = ( )

F = =2 .808

³ SCR N K

( )

- 2.5375 40 4

( )

-

3

Pour une 50 d'observations et un risque de première espèce deá =5% on a: F 3 = 2.808 ö 3 = 6.73.

On accepte ³

H₀ , le modèle 3 n'est pas le »bon» modèle, on doit effectuer à nouveau le test de non

stationnarité dans le modèle 2.

2-On teste la racine unitaire dans le modèle2 incluant une constante et un terme différencié retardé:

ÄLBAC = ö LBA C - + c + Ä LBAC + å _t .

t t 1 t - 1

On teste : H₀: ö = 0 vs H₁: ö < 0

t _ö = - 1.162102 > 2

C_á = -2.93 pour un seuil á = 5% (-2.93 pour 50 observations). Donc pour un

à = 0

niveau de risqueá =5% , on accepte l'hypothèse nul de racine unitaire( ö = 0). 2-comme H₀ est acceptée on teste: ²

H : (c;ö) = (c;0) contre H 1

2

0

( )

SCR _C SCR

2, 2

-

( )

N K

-

2 = ( )

3.71 2.83 2

-

2.83 40 3

( )

-

F₂ =

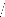
=5.7523.

2

SCR

Pour une taille de 50 et un risque de première espèce deá = 5% on a: F₂ = 5.75 ö ₂= 5.13 On rejette l'hypothèse ²

H₀ . Dans ce cas, le modèle 2 est le »bon» modèle, et la série LBAC _t est non stationnaire (I(1)+C ou I(d)+C ), d > 1.

Vérification de l'ordre d'intégration:

Figure 4 : graphique de la série DLBAC.

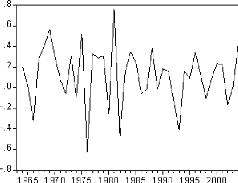
D'après le graphique de la série du nombre de bacheliers en différence première, il semble que la série soit stationnaire.

Le test Augmented Dickey Fuller (ADF):

On teste la racine unitaire dans le modèle suivant:

Ä LBAC = ö Ä LBAC - + c + Ä LBAC + t

2 ² í

t 1

t t - 1

On teste : H₀: ö = 0 vs H₁: ö < 0

t _ö = - 5.33666 < 2

C_á = -2.93 pour un seuil á =5% (-2.93 pour 50 observations). Donc, pour un

à = 0

niveau de risqueá =5% , on refuse l'hypothèse nul de racine unitaire( ö = 0). Autrement dit : la série ÄLBA C _t est stationnaire I(0)+C.

Analyse des résidus d'estimation de la série LBAC : On analyse le résidu d'estimation å_t du modèle : t

Ä LBAC = c + î ÄLBA C t - 1 + å t

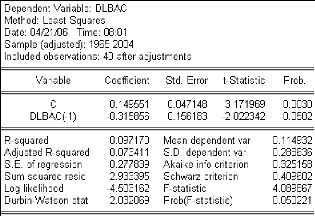
Figure 5 : résultats d'estimation du modèle.

-La constante t risqueá = 5% , ^àC= 0 -Le coefficient

=

Cà

est =

significativement non nul pour 0. 149551 =3.17 1.96 inférieur à 5%) (Prob

un un

niveau niveau

de de

î

ó àC0.047148 est significativement non nul pour

risqueá = 5% , à= 0 t î

à î

0.3 15856 0. 156183

=2.02 1.96

(Prob ? 5%).

à

ó î

Graphiques de la série originale et la série générée:

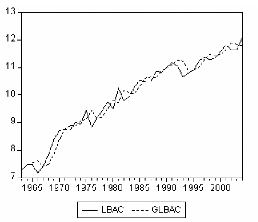
On compare ici, le graphique de la série originale (LBAC) et la série générée (GLBAC,

avec: t t

GLBA C = LBA C + 0.149 - 0.31 6ÄLBA C t - 1 + e_t), pour s'assurer que notre démarche de

stationnarisation nous a donné bons résultas.

Figure 5: graphiques de LBAC et GLBAC.

Analyse du corrélogramme des résidus d'estimation:

Figure 6: corrélogramme des résidus d'estimation

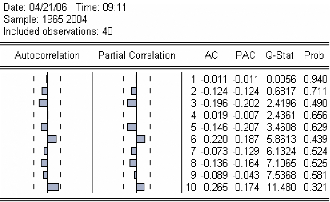
On remarque que pour les retards h=1,... ,10 , les termes du corrélogramme sont à l'intérieur de

l'intervalle de confiance (représentées par des traits pointillés horizontaux).

Le test de Ljung -Box nous indique que toutes les autocorrélations sont significativement nulles:

H : ñ = ñ = ñ = = ñ 10 = 0 Contre H 1 : ? j ? [ 1,10 ] tq : ñ j = 0

0 1 2 3

10 2

ñ à

QN N

' = + =

( )

2 11.48

k < 2

÷ ₁₀(10) = 18.307 .on accepte H₀ en plus (Prob pour

h -

k = 1 N K

h=1, ... ,10 supérieurs au seuil de 5%).Par conséquent, le résidu peut être assimilé à un processus bruit blanc.

En définitive : la série LBAC _t est non stationnaire (I(1)+C). Dés lors, pour rendre la série stationnaire

il faut la différencier une fois.

La série SLBA C _t issue de la série LBAC _t et quant à elle,stationnaire. On note :

SLBAC _t =ÄLBAC t

5. Analyse de la série du nombre de diplômés :

Cette série correspond au nombre de diplômés (DIP) de 1963 à 2004.

Données, Ministère de l'enseignement supérieur et de la recherche scientifique, annuelles, 1963 à 2004, 42 observations.

Evaluation graphique de la non stationnarité :

Série brut :

Figure 1: graphique de la série DIP.

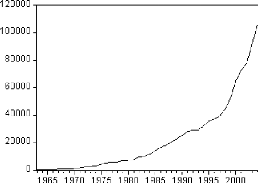
Le graphique de la série du nombre de diplômés fait ressortir une tendance globale à la hausse. Il semble donc que la série soit non stationnaire.

Série transformée :

Afin de stabiliser la série, on lui applique une transformation logarithmique.

Figure 2: graphique de la série LDIP.

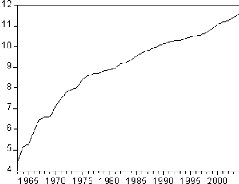
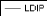
De même, Le graphique de la série logarithme fait ressortir une tendance globale à la hausse. Il semble donc que la série soit non stationnaire.

Analyse des autocorrélations et autocorrélations partielles:

Figure 3 : corrélogramme de la série LDIP.

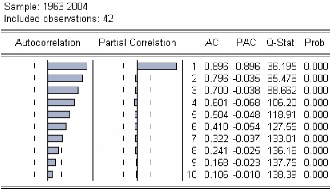
Le premier graphique (corrélogramme) représente les autocorrélations d'ordre h=1,... ,10 , et le
deuxième (corrélogramme partiel) les autocorrélations partielles d'ordre h=1,...,10 . Les colonnes AC

et PAC reportent les valeurs numériques correspondantes. Q-Stat est la valeur de la statistique de LjungBox et Prob la p-value associée.

On remarque que jusqu'au retard h=7 les termes du corrélogramme sont à l'extérieur de l'intervalle de confiance (représentées par des traits pointillés horizontaux).On constate aussi que toutes les autocorrélations sont significativement différentes de 0

(Prob pour h=1,... ,10 inférieures au seuil de 5%) et décroissent très lentement. Ceci est aussi

caractéristique d'une série non stationnaire.

Le test Augmented Dickey Fuller (ADF): Choix du nombre de retards optimal P :

Dans Eviews 5.0, la spécification qui minimise les critères d'information Akaike (AIC) et Schwarz(SC), est faite automatiquement dans le cadre de la procédure de test de racine unitaire. Compte tenu du nombre d'observations disponibles on choisis p_Max =4.

	Modéle1	Modéle2	Modéle3
AIC	4	2	2
SC	4	2	2

Selon le principe de parcimonie, on retient p=2 retards.

Stratégie du test:

1-On estime le modèle3 incluant une constante, un trend, et deux termes différenciés retardés:

Ä = t + + + Ä - + Ä - +

LDIP ö LDIP c â t î LDIP t î LDIP t å t

t - 1 1 1 2 2

On teste : H₀: ö = 0 vs H₁: ö < 0

t _ö = -6.408049 < 3

C á = -3.50 pour un seuil á =5% (-3.50 pour 50 observations). Donc, pour un

à = 0

niveau de risqueá =5% , on refuse l'hypothèse nul de racine unitaire( ö = 0).

comme H₀ est refusée on teste: H₀ :â = 0 vs H₁ :â ? 0

Le coefficient de la tendance est significativement non nul pour un niveau de risqueá =5%.

à

0.027470

ó à 0.005474

â

5.017 > 1.96. (Prob inférieure à 5%)

â

tâà = 0

Le modèle 3 est le »bon» modèle, pour tester la racine unitaire. Par conséquent, la série LDIP _t est TS. Estimation du modèle :

On estime le modèle : t - 1 1 1 2 2

LDIP ä LDIP c â t î LDIP t î LDIP t å t

= t + + + Ä - + Ä -+

Figure 5: estimation du modèle.

-Le coefficient ä est significativement non nul pour un niveau de risqueá =5%.

à

0.730770

t 17.39 1.96

à= 0 = = =

^ä ó à 0.042014

ä

ä

(Prob inférieure à 5%).

-Le coefficient de la tendance est significativement non nul pour un niveau de risqueá =5%.

à

0.027470

ó à 0.005474

â

5.017 > 1.96 (Prob inférieure à 5%)

â

tâà = 0

-La constante est significativement non nulle pour un niveau de risqueá =5%.

Cà 2.073594 t 7.25 1.96 = = = ^àC= 0 óC à0.285877

(Prob inférieure à 5%)

-Le coefficient î₁ n'est pas significativement non nul pour un niveau de risqueá =5%.

à

1 0.003565

t 0.031 1.96

= = =

î à = 0

1 ó à 0.113581

î 1

î

(Prob supérieure à 5%).

-Le coefficient î₂ est significativement non nul pour un niveau de risqueá =5%.

à

2 0.313388

t 2.89 1.96

= = =

î à = 0

2 ó à 0.108198

î 2

î

(Prob inférieure à 5%).

Par conséquent, la série LDIP _t peut être estimé par :

LDIP LDIP t LDIP t e _t .

t = + t + ? Ä - +

2.07 0.73 - 0.027 0.31 2

1

Graphiques de la série originale et la série générée:

On compare ici, le graphique de la série originale (LDIP) et la série générée (GLDIP, avec: t

LDIP LDIP t LDIP t e _t ), pour s'assurer que notre démarche de

= + t + ? Ä - +

2.07 0.73 - 0.027 0.31 2

1

stationnarisation nous a donné bons résultas.

Figure 5: graphiques de LDIP et GLDIP.

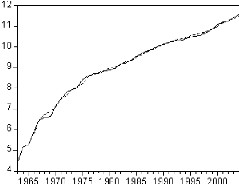
Analyse du corrélogramme des résidus d'estimation:

On analyse le résidu d'estimation å_t du modèle: t ä - 1 â î 2 2 å .

LDIP LDIP c t LDIP t t

= t + + + Ä - +

Figure 6: corrélogramme des résidus d'estimation.

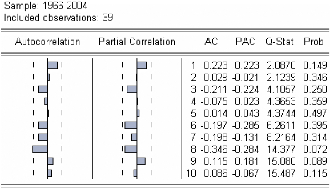
On remarque que pour les retards h=1,... ,10 , les termes du corrélogramme sont à l'intérieur de

l'intervalle de confiance (représentées par des traits pointillés horizontaux).

Le test de Ljung -Box nous indique que toutes les autocorrélations sont significativement nulles:

H : ñ = ñ = ñ = = ñ 10 = 0 Contre H 1 : ? j ? [ 1,10 ] tq : ñ j = 0

0 1 2 3

10 2

ñ à

QN N

' = + =

( )

2 15.487

k < 2

÷ ₁₀(10) = 18.307 .on accepte H₀ , en plus (Prob pour

h -

k = 1 N K

h=1, ... ,10 supérieurs au seuil de 5%).Par conséquent, le résidu peut être assimilé à un processus bruit blanc.

En définitive, la série LDIP _t est non stationnaire de type TS. Dés lors, on considère la série stationnaire

SLDIP _t issue de la série LDIP _t engendré par :

SLDIP =LDIP -(2.07+0.73LDIP t - 1 +0.027t).

t t

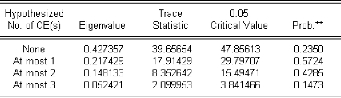
2.2.b. Résultats d'estimation des modèles :

1. Estimation du premier modèle VAR:

Afin de déterminer si les scolarisés, les bacheliers et les dépenses d'éducation ont une implication dans la croissance économique, nous considèrerons les quatre séries :

- SCO : Effectifs scolarisés à tous le niveaux confondus (processus DS, I(1)+T+C ), - BAC : Nombre de bacheliers (processus DS, I(1 )+C ),

- DEP : Dépenses d'éducation (processus DS, I(1)),

- PIB : Produit intérieur brut (processus DS, I(1) ).

Après avoir procédé à une transformation logarithmique puis à leurs stationnarisation (les séries transformées et stationnarisées seront précésées par les lettre L et S respectivement), on estime par la suite le modèle VAR.

Choix du nombre de retards :

On utilise les critères d'information AIC et de Schwarz

	AIC	SC
P=1	-9.574658	-8.712770
P=2	-9.579533	-8.012153
P=3	-9.905313	-7.618008

Selon le principe de parcimonie, on retient p=1 retard.

Les séries SCO, BAC, DEP, et PIB étant des processus DS intégrées de même ordre 1. Il faut vérifier qu'il n'y a pas de cointégration en niveau entre ces variables.

Test de cointégration :

Les séries initiales étant caractérisées par une tendance générale à la hausse, nous choisissons la spécification 3 (tendance dans les données, constante dans la ou les relations de cointégration) avec 1 retards.

Figure 1 : Test de Cointégration entre LPIB, LBAC, LDEP, LSCO.

(Statistique de Johansen)

On teste : 0

H : r = 0 contre H₁ : r > 0. la statistique de Johansenëtrace(0) = 39.6547.85 au seuil 5%. Le test indique que les quatre séries ne sont pas cointégrées.

Résultats d'estimation :

Le VAR estimé s'écrit :

e1,t

+ e2,t e3,t e4,t

SLSCO 0.001 0.146 0.002 0.004 0.001 SLSCO

t t 1

-

SLDEP 0.014 1.565 0.097 0.016 0.460 SLDEP

- -

t t 1

-

= +

SLBAC 0.106 4.313 0.280 0.313 1.792 SLBAC

- - -

t t 1

-

SLPIB0.047 0.135 0.0002 0.022 0.210 SLPIB

- -

t t - 1

Vérification de la stabilité du VAR :

Figure 3 : vérification de la stabilité de VAR.

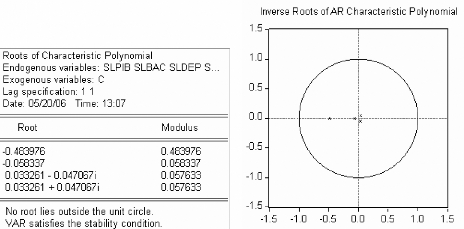
La première colonne donne les l'inverse des racines associées à la partie AR, et la deuxième colonne leurs modules. L'inverse des 4 racines associées à la partie AR appartient au disque unité complexe. Le VAR est par conséquent stationnaire.

Analyse des résidus :

Figure 4 : graphique des autocorrélations et des corrélations croisées des résidus.

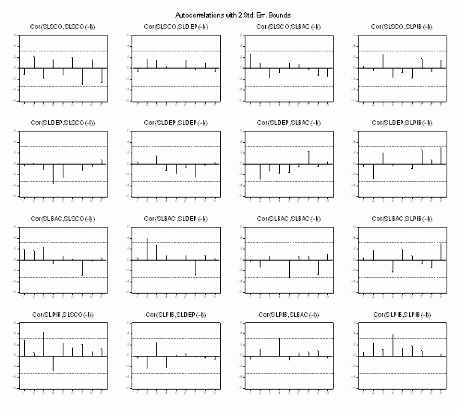
Les graphiques sur la diagonale (corrélogrammes) représentent les autocorrélations d'ordre h=1,... ,9 , et les autres graphiques (corrélogrammes croisées) représentent les corrélations croisées d'ordre h=1,... ,9 . On remarque que pour les retards h=1,... ,9, les termes des corrélogrammes et des corrélogrammes croisées sont à l'intérieur de l'intervalle de confiance (représentées par des traits pointillés horizontaux).Par conséquent, chaque résidu peut être assimilé à un processus bruit blanc.

Etude des fonctions de réponse :

Les influences simultanées entre les différentes variables sont déterminées par les fonctions de réponses impulsionnelles suivantes :

Figure 4 : Fonctions de Réponses Impulsionnelles.

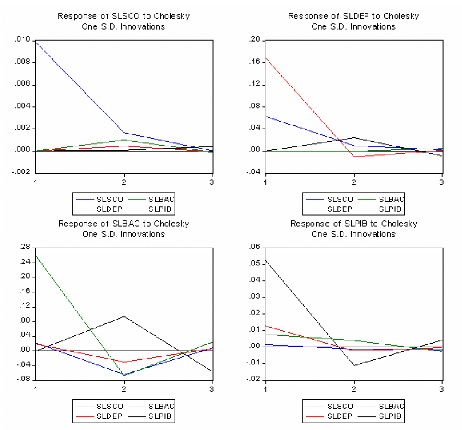
De façon générale, nous remarquons que les chocs sont transitoires, c'est-à-dire que les variables retrouvent leur équilibre de long terme au bout de 3 périodes. Toutes les fonctions de réponse tendent vers 0, ce qui confirme que le modèle VAR est stationnaire.

Conséquences d'un choc sur La variable SCO:

L'impact d'un choc sur la variable SCO est égal à 0.009847, il se répercute ensuite sur les 4

variables:

- La variable DEP est affectée d'une manière positive (0.000446) à la éme

2période, puis elle décroît pour

atteindre son niveau d'équilibre,

- La variable BAC est affectée d'une manière positive (0.000998) à la éme

2période, puis elle décroît pour

atteindre son niveau d'équilibre,

- Le PIB semble ne pas être affecté par ce choc, et reste sur son sentier d'équilibre.

Conséquences d'un choc sur La variable DEP:

L'impact d'un choc sur la variable DEP est égal à 0.168211, il se répercute ensuite sur les 4 variables: - La variable SCO et Le PIB sont affectées d'une manière positive à la éme

1 période et la éme

2période

respectivement mais décroissent rapidement pour retrouver leur niveau d'équilibre,

- La variable BAC semble ne pas être affecté par ce choc, et reste sur son sentier d'équilibre. Conséquences d'un choc sur La variable BAC:

L'impact d'un choc sur la variable BAC est égal à 0.2587, il se répercute ensuite sur les 4 variables: - Le PIB est affecté d'une manière positive (0.093) la éme

2période, puis décroît et retrouve son niveau

d'équilibre,

- L variables DEP et SCO sont affectées d'une manière positive et décroissent jusqu'à la éme

2période,

puis ils croissent pour atteindre leur niveau d'équilibre.

Conséquences d'un choc sur le PIB:

L'impact d'un choc sur la variable BAC est égal à 0.0522, il se répercute ensuite sur les 4 variables:

- Les variables DEP et BAC sont affectées d'une manière positive, mais décroissent rapidement pour retrouver leur niveau d'équilibre.

- La variable SCO semble ne pas être affecté par ce choc et reste sur son sentier d'équilibre. Etude de la causalité :

On étudie la causalité entre le PIB, la variable BAC, la variable DEP, et la variable SCO.

Figure 5 : causalité à la Granger.

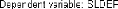
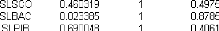
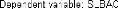
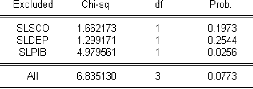
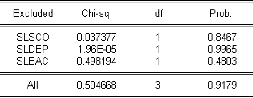
Dans la première équation du modèle VAR:

SLSCO = 0.001 SLPIB + 0.004 SLBAC + 0.002 SLDEP + 0.146 SLSCO _t-1 + 0.001 + e _1,t .

t t-1 t-1 t-1

au risque 5% les variables PIB, BAC , et DEP ne causent pas la variable SCO ni individuellement(prob supérieures à 5%), ni conjointement (ALL: prob supérieures à 5%).

Dans la seconde équation du modèle VAR :

SLDEP = 0.460 SLPIB - 0.016 SLBAC - 0.097 SLDEP + 1.565 SLSCO _t-1 + 0.014 +e _2,t .

t t-1 t-1 t-1

au risque 5% les variables PIB, BAC , et SCO ne causent pas la variable DEP ni individuellement(prob supérieures à 5%), ni conjointement (ALL: prob supérieures à 5%).

Dans la troisième équation du modèle VAR:

SLBAC = 1.792 SLPIB - 0.313 SLBAC - 0.280 SLDEP - 4.313 SLSCO _t-1 + 0.106 + e _3,t .

t t-1 t-1 t-1

au risque 5% les variables DEP et SCO ne causent pas la variable BAC (prob supérieures à 5%). Par contre le PIB cause la variable BAC (prob inférieures à 5%), mais conjointement ces trois variables ne causent pas la variable BAC (prob supérieures à 5%).

Dans la quatrième équation du modèle VAR:

SLPIB = - 0.210 SLPIB + 0.022 SLBAC + 0.0002 SLDEP - 0.135 SLSCO _t-1 + 0.047 + e _4,t .

t t-1 t-1 t-1

au risque 5% les variables BAC ,DEP, et SCO ne causent pas le PIB ni individuellement(prob supérieures à 5%), ni conjointement (ALL: prob supérieures à 5%).

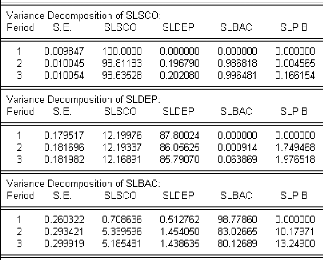
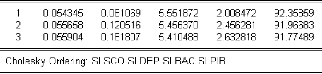
Circuit de causalité:

Figure 6 : circuit de causalité.
+

PIB BAC

- la direction désigne le sens de la causalité.

- le signe (+) peut être obtenu à partir de la réponse au choc su le PIB.

Analyse de la décomposition de la variance :

Elle nous permettra de voir dans quelle mesure les variables ont une interaction entre elles, et dans quel sens l'impact du choc est le plus important.

Figure 7 : Décomposition de la variance.

Décomposition de la variance de la variable SCO :

- La variance de l'erreur de prévision de la variable SCO est due à 98% à ses propres innovations, et à 1% à celle de la variable DEP.

Décomposition de la variance de la variable DEP :

- Pour la éme

1période: La variance de l'erreur de prévision de la variable DEP est due à 88% à ses

propres innovations, et à 12% à celle de la variable SCO.

-Pour les périodes 2 et 3 : elles est due à 86% à ses propres innovations,à 12% à celle de la variable SCO,et à 2% au PIB.

Décomposition de la variance de la variable BAC :

- Pour la éme

1période: la variance de l'erreur de prévision de la variable BAC est due à 99% à ses

propres innovations.

- Pour la éme

2période: la variance de l'erreur de prévision de la variable BAC est due à 83 % à ses

propres innovations, à 5% à celle de la variable SCO, et à 10% au PIB.

- Pour la éme

3période: la variance de l'erreur de prévision de la variable BAC est due à 80 % à ses

propres innovations, à 5% à celle de la variable SCO, et à 13% au PIB.

Décomposition de la variance du PIB:

- La variance de l'erreur de prévision du PIB est due à 92% à ses propres innovations et à 2% à celle de la variable BAC, et à 5% à celle de la variable DEP .

2. Estimation du deuxième modèle VAR:

Afin de déterminer si les diplômés ont une implication dans la croissance économique, nous considèrerons les deux séries :

- DIP : nombre de diplômés du supérieur (processus TS),

- PIB : produit intérieur brut (processus I(1) ).

Après avoir procédé à une transformation logarithmique des séries, puis à leurs stationnarisation (les séries transformées et stationnarisées seront précédées par les lettres L et S), on estime par la suite le modèle VAR.

Choix du nombre de retards :

On utilise les critères d'information AIC et de Schwarz

	AIC	SC
P=1	-5 .100696	-4.842129
P=2	-5.026720	-4.835370
P=3	-5 .616068	-5.000255
P=4	-5.770901	-4.971008
P=5	-5.850764	-4.863118

Selon le principe de parcimonie, on retient p=3 retards.

Les séries DIP et PIB étant des processus TS et DS respectivement. Il n'y a donc pas de risque de cointégration entre ces variables.

Résultats d'estimation: Le VAR estimé s'écrit:

SLDIP 0.02 0.22 0.34 SLDIP 0.25 0.09 SLDIP 0.20 0.98 SLDIP e

t 1,t

- - -

t - 1 t - 2 t - 3

= + + + +

SLPIB0.030.08 0.11 SLPIB 0.22 0.16 SLPIB 0.07 0.16 SLPIB e

t 2,t

- - -

t 1

- t - 2 t - 3

Vérification de la stationnarité du VAR :

Figure 3 : vérification de la stabilité de VAR.

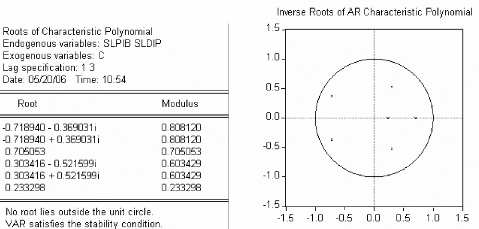
La première colonne donne les inverses des racines associées à la partie AR (les valeurs propres), et la deuxième colonne leurs modules. L'inverse des 6 racines associées à la partie AR appartient au disque unité complexe. Le VAR est par conséquent stationnaire.

Analyse des résidus :

Figure 4 : graphique des autocorrélations et des corrélations croisées des résidus.

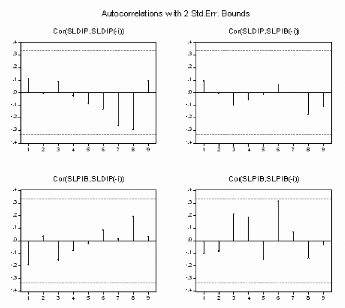
Les graphiques sur la diagonale (corrélogrammes) représentent les autocorrélations d'ordre h=1,... ,9 , et
les autres graphiques (corrélogrammes croisées) représentent les corrélations croisées d'ordre h=1,... ,9 .
On remarque que pour les retards h=1,... ,9, les termes des corrélogrammes et des corrélogrammes
croisées sont à l'intérieur de l'intervalle de confiance (représentées par des traits pointillés
horizontaux).Par conséquent, chaque résidu peut être assimilé à un processus bruit blanc.

Etude des fonctions de réponse :

Les influences simultanées entre les différentes variables sont déterminées par les fonctions de réponses impulsionnelles suivantes :

Figure 4 : Fonctions de Réponses Impulsionnelles.

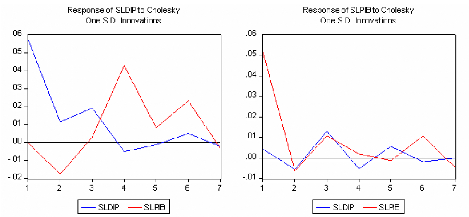
De façon générale, nous remarquons que les chocs sont transitoires, c'est-à-dire que les variables retrouvent leur équilibre de long terme au bout de 7 périodes. Toutes les fonctions de réponse tendent vers 0, ce qui confirme que le modèle VAR est stationnaire

Conséquences d'un choc sur La variable DIP:

L'impact d'un choc sur la variable DIP est égal à 0.05745 1, il se répercute ensuite sur les 2 variables: - Le PIB est affecté d'une manière positive et décroît jusqu'à la éme

2période, puis il croît et atteint son

maximum à la éme

4 période. Par la suite il décroît et retrouve son niveau d'équilibre.

- La variable DIP est affectée d'une manière négative (-0.0 17554) à la éme

2période, puis elle croît et

atteint son point maximale à la éme

4période, par la suite elle décroît et retrouve son niveau

d'équilibre.

Conséquences d'un choc sur La variable PIB:

L'impact d'un choc sur le PIB est égal à 0.05 1728, il se répercute ensuite sur les 2 variables: - Le PIB est affecté d'une manière positive (0.051728) et décroît jusqu'à la éme

2période, puis il croît

jusqu'à la éme

3 période, par la suite il décroît et retrouve son niveau d'équilibre.

- La variable DIP est affectée d'une manière positive (0.004434) et décroît jusqu'à la éme

2période, puis

elle croît et atteint son point maximale à la éme

3période, par la suite elle décroît et retrouve son niveau

d'équilibre.

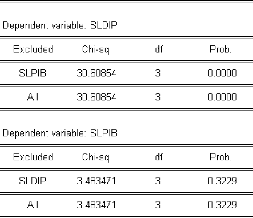
Etude de la causalité :

On étudie la causalité au sens de Granger entre le PIB et la variable DIP.

Figure 5 : causalité à la Granger.

Dans la première équation du modèle:

SLDIP = - 0.02 - 0.33 SLPIB + 0.09 SLPIB + 0.98 SLPIB + 0.22 SLDIP t-1

t t-1 t-2 t-3

+0.24 SLDIP _t-2 - 0.20 SLDIP _t-3 + e_1,t . au seuil 5% : le PIB cause la variable DIP (prob inférieures à 5).

Dans la seconde équation du modèle:

SLPIB = 0.03 - 0.11 SLPIB + 0.16 SLPIB + 0.16 SLPIB - 0.09 SLDIP t-1

t t-1 t-2 t-3

+ 0.22 SLDIP _t-2 - 0.07 SLDIP t-3 +e2,t .

au seuil 5% : la variable DIP ne cause pas le PIB (prob inférieures à 5%).

Circuit de causalité:

Figure 6 : circuit de causalité.

+

PIB DIP

- la direction désigne le sens de la causalité.

- le signes (+) peut être obtenu à partir des réponses au chocs.

~

104

~

Analyse de la décomposition de la variance :

Va nous permettre de voir dans quelle mesure les variables ont une interaction entre elles, et dans quel sens l'impact du choc est le plus important.

Figure 7 : Décomposition de la variance.

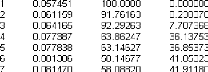
Décomposions de la variance de la variable DIP:

- Pour les périodes 2 et 3: la variance de l'erreur de prévision de la variable DIP est due à 92% à ses propres innovations, et à 8% à celle du PIB.

- Pour les périodes 4, 5,6 et 7: la variance de l'erreur de prévision de la variable DIP est due en moyenne à 60% à ses propres innovations, et à 40% à celle du PIB.

Décomposions de la variance du PIB:

-Pour la période 1: la variance de l'erreur de prévision du PIB est due à 99 % à ses propres innovations et à 1% à celle de la variable DIP.

-Pour la période 2: la variance de l'erreur de prévision du PIB est due à 98 % à ses propres innovations et à 2 % à celle de la variable DIP.

-Pour les périodes 3: la variance de l'erreur de prévision du PIB est due à 93 % à ses propres innovations et à 7 % à celle de la variable DIP.

-Pour les périodes 5, 6 et 7: la variance de l'erreur de prévision du PIB est due à 91 % à ses propres innovations et à 9 % à celle de la variable DIP.

Interprétation économique de l'ensemble des résultats :

Afin d'interpréter économiquement les résultats de l'analyse des fonctions de réponses impulsionnelles, et les tests de causalités dans les deux modèles Var, il est utile de rappeler que les fonctions de réponses impulsionnelles représente l'effet d'un choc d'une innovation sur les valeurs courantes et futures des variables endogènes. Ainsi, l'explication de l'interaction entre les variables, sera en fonction de l'environnement économique de l'année où le choc a été appliqué (2004) et les années future (les années après 2004). Par contre, les tests de causalités englobent toute la période de l'étude. Donc, notre interprétation tiendra en compte de l'histoire économique de l'Algérie indépendante.

Par conséquent, on peut dire que, l'augmentation du nombre de bacheliers dans le 1^er modèle VAR et celui du nombre de diplômés dans le 2^nd modèle VAR suite à une augmentation significative de la croissance économique, peut être due à un phénomène d'anticipation, c'est-à-dire que, la croissance future augmente le rendement de l'éducation, car les revenus futures seront plus élevés que les revenus sacrifiés aujourd'hui. Ainsi, si les Algériens anticipent que la croissance sera élevée, ils s'éduqueront davantage immédiatement.

Les deux relation de causalités positives trouvées entre la croissance économique et les bacheliers d`une part, et le PIB et les diplômés d'autre part, sont dues essentiellement aux investissements effectués par l'Algérie dans le passé. Ces derniers ont permis la créations et le développement des structures d'accueils des étudiants, ce qui à engendré la croissance au fil du temps du nombre de bacheliers et de diplômés.

En combinons les différents résultats issus de l'analyse des chocs, des tests de causalités, et de la décomposition de la variance de l'erreur de prévision on montre que :

Dans le 1 modèle VAR,

· Une augmentation significative des effectifs scolarisés n'a pas d'impact sur le PIB, sa variance de l'erreur de prévision est due à 98% à ses propres innovations,

· Une augmentation significative des dépenses d'éducation conduit à une augmentation des effectifs scolarisés et de celle du PIB pendant les 2 années qui suivent le choc, mais cet impact et non significatif car on n'a pas trouvé de relations de causalités entre ces variables,

· Une augmentation significative de la richesse du pays, conduit dans la première année, à une croissance des dépenses de l'éducation et du nombre de bacheliers, puis à leur décroissance dans la 2ème année. Cet impact est significatif pour la variable BAC, car ont a trouver une causalité entre la croissance économique vers le nombre de bacheliers. Néanmoins, cette relation de causalité positive reste très fragile, la variable PIB participe seulement à hauteur de 10% dans la variance de l'erreur de prévision de la variable BAC,

· Une croissance significative du nombre de bacheliers conduit à l'augmentation de la croissance économique dans les 2 ans qui suivent le choc. Mais cet impact est non significatif, car on n'a pas trouvé de relation de causalité de la variable BAC vers la croissance économique, et en plus la variance de l'erreur de prévision du PIB est due à 92 % à ses propres innovations.

Dans le 2^ème modèle VAR,

· Une augmentation significative du nombre de diplômés, conduit ce dernier à décroître dans la 2ème année, puis à croître est décroître encore dans les années qui suivent jusqu'a l'extinction du choc après une période de 7 ans. Cette dynamique du nombre de diplômés est la même que c'elle du PIB. Mais, cette interaction entre les diplômés est la croissance économique reste non significative car, on a pas trouvé de relation de causalité des diplômés vers le PIB.

· Une augmentation de la croissance économique, conduit le PIB et le nombre de diplômés à suivre la même dynamique. Cette interaction parfaite entre la variable PIB et DIP laisse penser à l'existence d'une relation de causalité positive entre la croissance économique et le nombre de diplômés. Cette intuition est vérifiée par les résultats des tests de causalités, qui montrent que la croissance économique cause le nombre de diplômés, et par la décomposition de la variance de l'erreur, qui montre que, la croissance économique explique à hauteur de 8% de la variance de l'erreur de prévision des diplômés dans les 2 première années, puis 40% à partir de la 3 années.