4.1.2 Présentation du modèle
Les variables ainsi définies, nous pouvons construire
un modèle logistique dichotomique admettant comme variable
expliquée la probabilité 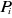 d'apparition de l'événement : « l'individu d'apparition de l'événement : « l'individu
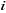 est pauvre». Ainsi, on postule le modèle suivant : est pauvre». Ainsi, on postule le modèle suivant :
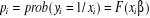
Où la fonction 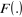 désigne la fonction logistique, désigne la fonction logistique,
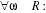 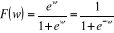
Avec 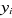 , la variable explicative qui prend la valeur 1 si l'enfant , la variable explicative qui prend la valeur 1 si l'enfant 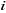 est pauvre et 0 sinon. est pauvre et 0 sinon.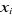 , le vecteur des caractéristiques sociodémographiques de
l'enfant, de son ménage de résidence et de son environnement. , le vecteur des caractéristiques sociodémographiques de
l'enfant, de son ménage de résidence et de son environnement.
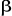 est le vecteur des paramètres du modèle. Les valeurs
numériques de ses composantes est le vecteur des paramètres du modèle. Les valeurs
numériques de ses composantes 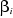 associées aux variables explicatives associées aux variables explicatives 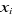 n'ont pas d'interprétation économique directe en raison du
problème de la normalisation de la variable résiduelle.
Cependant, leur signe est la seule information réelle directement
utilisable. Ce signe indiquera dans le cas précis de notre modèle
si la variable associée à ce paramètre influence à
la hausse ou à la baisse la probabilité qu'un enfant soit
pauvre. n'ont pas d'interprétation économique directe en raison du
problème de la normalisation de la variable résiduelle.
Cependant, leur signe est la seule information réelle directement
utilisable. Ce signe indiquera dans le cas précis de notre modèle
si la variable associée à ce paramètre influence à
la hausse ou à la baisse la probabilité qu'un enfant soit
pauvre.
Pour compléter l'analyse, il est possible de calculer
les effets marginaux mesurant la sensibilité de la probabilité
qu'un enfant soit pauvre par rapport aux variations dans les variables
explicatives.
| 


