2.2 La valve aortique
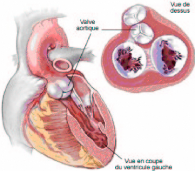
FIG. 2.2Shémas de la valve aortique
La valve aortique qui assure l'écoulement continu de
sang du ventricule gauche dans l'aorte, est située à la sortie du
ventricule gauche et constituée de trois feuillets semi-lunaires
très flexibles qui sont attachés à la racine aortique par
le point commissure, ces derniers s'emboîtent parfaitement lorsque la
valve est fermée. Voir la figure 2.2.
En systole le ventricule se contracte, la pression
intra-ventriculaire dépasse la pression dans l'aorte (Pv > Pa) ce qui
ouvre la valve en permettant la sortie du sang.Voir figure 2.3.
En diastole le coeur se relache, la pression diminue (Pv <
Pa) la valve se referme sans fuite pour empêcher tout flux sanguin vers
le ventricule.
Le mécanisme de l'ouverture et la fermeture de la valve
aortique est lié aux variations de pression entre les deux
cavités.
Certaines malformations de la valve aortique peuvent
gêner le fonctionnement du coeur, pendant la fermeture et l'ouverture, la
valve devient incontinente et une fuite aortique (reflux de sang de l'aorte
vers le ventricule) apparaît. A l'inverse, si la valve ne s'ouvre pas
complètement, une petite quantité de sang ne peut pas sortir. On
parle alors de rétrécissement.
Cela entraîne une surcharge de travail pour le coeur
(ventricule gauche) qui doit assurer un débit suffisant pour l'organisme
malgré la fuite. Cette surcharge peut parfois conduire à une
insuffisance cardiaque.
Ces troubles peuvent obliger le remplacement de la valve
défectueuse par une valve artificielle ou une valve provenant d'un coeur
de porc.
|
CHAPITRE 2. LE COEUR ET LA CIRCULATION SANGUINE
|
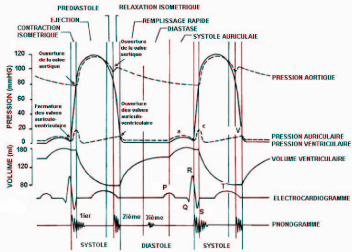
FIG. 2.3Cycle cardiaque
2.3 propriétés
Le tissu de la valve aortique est une structure
élastique et linéaire, les propriétés
mécaniques sont prisent du modèle de Grande [2] ont
été utilisées pour la racine aortique, voir le tableau
2.3.
Tab. 2.2 - Les epaisseurs du tissu utilisé pour les
feuillets et la racine de la valve, pris du modèle de Grande
.
Epaisseur (mm)
|
gauche et droit (mm)
|
sans coronnaire (mm)
|
|
Bord d'attachement
|
1.16
|
0.155
|
|
Belly
|
0.18 - 0.58
|
0.18 - 0.58
|
|
Bord libre
|
1.53
|
1.96
|
|
Nodulus of aranti
|
2.06
|
2.75
|
|
CHAPITRE 2. LE COEUR ET LA CIRCULATION SANGUINE
|
Par contre les feuillets sont trop raides pour s'ouvrir sous
le chargement physiologique de pression ce qui explique son comportement
non-linéaire, Thubrikar [2]. Les propriétés
mécaniques du tissu utilisées dans le modèle
élastique de Thubrikar, sont énumérées dans le
tableau 2.3.
Tab. 2.3Propriétés mécaniques
utilisées pour le tissu de la valve et la racine aortique, pris de
l'étude par éléments finis du modéle de
Thubrikar
.
Propriété
|
Valve aortique
|
Racine aortique
|
|
Ecirc(KPa)
|
220,000
|
334,000
|
|
Erad(KPa)
|
200,000
|
-
|
|
Elong(KPa)
|
-
|
350,000
|
|
?xy
|
0,450
|
0,450
|
|
?zy
|
0,450
|
0,450
|
|
?xz
|
0,450
|
0,429
|
Le module de Young et le coefficient de Poisson pour le mur et
les feuillets aortiques ont été obtenus à partir de
l'étude par éléments finis faite par Grande.
Tab. 2.4 - Propriétés mécaniques
utlisées pour le tissu des feuillets
.
Propriété
|
Feuillet
|
Mur aortique
|
|
Epaisseur(mm)
|
0,500
|
1,000
|
|
Comportement
|
Isotropique
|
Isotropique
|
|
Module de Young(MPa)
|
0,900
|
6,000
|
|
Coefficient de Poisson
|
0,450
|
0,450
|
Pour le cylindre à paroi mince (rapport,
rayon/épaisseur, > 10) soumis à la pression interne, l'effort
est uniforme à travers cette l'épaisseure. Cet effort est dit
effort de membrane, et dans la direction circulaire il est defini par la
relation suivante [8] :
Où p est la pression, r est le rayon du feuillet, e est
l'épaisseure du feuillet
| 


