B. L'équilibre de run bancaire
L'analyse offerte par Diamond et Dybvig indique la
fragilité des transactions bancaires basées sur des passifs
liquides et des actifs illiquides, mais elle ne prend pas en
considération l'équilibre dans le secteur bancaire. Cependant,
elle suppose que le portefeuille de la Banque (x, y) et le contrat de
dépôt (c1, c2) sont choisis à la date 0, dans l'attente que
la première répartition optimale sera atteinte. En d'autres
termes, la ruée à la date 1, s'elle se produit, est totalement
inattendu à la date 0. En prenant les décisions à la date
0 comme donnée, l'équilibre à la date 1 dans lequel la
ruée survient est facile à définir, mais ce n'est pas
pareil que de montrer qu'il existe un équilibre qui commence à la
date 0 où une ruée est prévue de se produire. Si les
banques anticipent la possibilité d'une ruée, leurs
décisions à la date 0 seraient différentes et cela,
à son tour, pourrait avoir une incidence sur la probabilité ou la
possibilité d'une ruée à la date 1. Ce dont on a besoin
est de considérer un équilibre qui décrit les
décisions cohérentes à toutes les trois dates. Dans ce
sens, le modèle nous fournit une justification cohérente de la
ruée bancaire comme faisant partie d'un équilibre qui inclut les
décisions prises à la date 0. Il procède en
établissant un certain nombre de faits ou de propriétés de
l'équilibre de ruée bancaire avant de décrire la situation
globale.
a. L'impossibilité de prévoir la
ruée bancaire
Notant d'abord au sujet de la construction d'un
équilibre de ruée bancaire que ce dernier ne peut pas se produire
avec probabilité 1. Si une ruée bancaire est certaine à la
date 0, la banque sait que chaque unité du bien investi dans l'actif
long sera r unités à la date 1. Si r <1, l'actif long
est dominé par l'actif court et la banque ne peut pas du tout investir
dans des actifs long. Si r = 1, les deux actifs sont identiques. Dans les deux
cas, le contrat de dépôt est optimal (c1, c2) = (1, 1) et il n'y a
pas de motif pour une ruée bancaire: les épargnants auront la
même consommation, qu'ils rejoignent le ruée ou pas. Donc, le
mieux que nous pouvons espérer est qu'une ruée bancaire se
produise avec probabilité positive.
b.

16
Le rôle des taches solaires (Sun
spots)
L'incertitude sur la ruée bancaire introduit un nouvel
élément dans la théorie. Dans le modèle actuel, il
n'y a aucune incertitude sur les agrégats fondamentaux, tels que les
rendements des actifs, la proportion de consommateurs de type 1, et ainsi de
suite. Le type d'incertitude que Allen et Galle considère ici est
endogène, dans le sens où elle n'est pas expliquée par les
chocs sur les fondamentaux du modèle. Pour expliquer une telle
incertitude, les justifications de ruée bancaire vont souvent être
appelées psychologie de foule. Les justifications modernes
l'expliquent comme le résultat de la coordination entre les personnes,
qui sont facilitées par des variables extérieures appelé
taches solaires, il suffit pour le moment de constater que
l'incertitude n'est pas expliquée par des chocs exogènes, mais
qu'elle est complètement compatible avec les exigences de
l'équilibre, à savoir que chaque individu ait la maximisation de
son utilité espérée et que les marchés
s'éclaircissent.
Le modèle commence par l'hypothèse que la
ruée bancaire apparait à la date 1 avec la probabilité 0
<ð <1. Pour être plus concret, le modèle présume
qu'il existe une variable aléatoire (taches solaires) qui prend deux
valeurs, disons, élevé et faible, avec des probabilités
ð et 1 - ð, respectivement. Lorsque la réalisation de la
variable aléatoire est élevée, les déposants
courent à la banque et inversement. Notez que la variable
aléatoire n'a pas d'effet direct sur les préférences ou
bien sur les rendements d'actifs. Il s'agit simplement d'un dispositif pour
coordonner les décisions des épargnants. Il est rationnel pour
les déposants de modifier leur comportement en fonction de la valeur de
la tache solaire simplement parce qu'ils s'attendent à ce que tout le
monde fasse pareil.
c. Le comportement de la banque en présence d'une
ruée bancaire
L'attente d'une ruée bancaire à la date 1 change
le comportement de la banque à la date 0. La banque doit choisir
habituellement un portefeuille (x, y) et proposer un contrat de
dépôt (c1, c2), mais elle le fait dans l'espoir que les flux de
consommation (c1, c2) ne seront atteints que si elle est solvable. Dans le cas
d'une ruée bancaire, d'autre part, le déposant typique recevra la
valeur du portefeuille liquidé rx + y à la date 1. Cela signifie
que
? avec une probabilité ð il y a une ruée et la
consommation du déposant est, rx + y quel que soit son type;
? avec une probabilité (1-ð) ë il n'existe pas de
ruée : le déposant est un consommateur de type 1, et sa
consommation à la date 1 est c1;
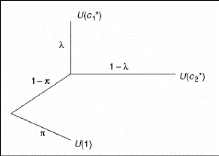

y' et avec une probabilité (1 - ð) (1 - ë), il
n'y a pas de ruée: le déposant est un consommateur de type 2, et
sa consommation à la date 2 c2.
Les résultats des décisions de la banque lorsque
les ruées sont anticipées sont illustrés dans la Figure
1
Figure 1. Résultats de l'équilibre lorsque les
ruées sont anticipées avec probabilité
Source : Allen et Gale (2008)
d. Le portefeuille optimal
Si c1 représente le paiement aux consommateurs de type 1
lorsque la banque est solvable et (x, y) désigne le portefeuille.
L'utilité espérée du déposant représentatif
est donc :
ðU(y + rx) + (1 - ð)
{ëU(c1) + (1 - ë)U (c2)}
.
Le modèle suppose maintenant que nous augmentons y
par un petit montant å> 0 et nous baissons x par ce même
montant. Nous augmentons ëc1 par å et réduisions (1 - ë)
c2 par Rå. Cela garantit que les contraintes de faisabilité sont
satisfaites à chaque date. Le changement d'utilité
espérée est donc le suivant :
ð U (1) (1 ð 0) ë U (
c ) (1 ë ) U ( c 2 )
ë U (1) (1 ë ) U ( R )
0 { }
+ - + - = + -
* *
1
Le portefeuille optimal doit donc satisfaire la condition de
premier ordre suivante :

18
ð U y rx 1 r 1 U c1 1 U c2 R
' ( ) ( ) ( ) ( ) ( ) ( )
+ - + - ð = - ð
' '
Si ð = 0, cela réduit alors à la condition
courante U (c1) = U (c2) R. Ces relations sont représentées dans
le graphique de la figure 2. Cette dernière condition tient à y*
tandis que la première tient à y** . Ainsi, la possibilité
d'une ruée augmente la valeur marginale y (court actif a un rendement
plus élevé qu'un actif long en état de faillite, si r
<1) et, par conséquent, augmente le montant de l'actif court tenue
dans le portefeuille.
Figure 2. La détermination du portefeuille
optimal lorsque la ruée est
possible
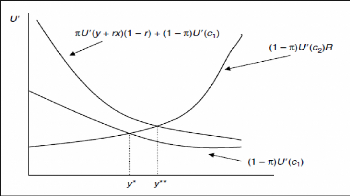
Source : Allen et Gale (2008)
e. Le contrat de dépôt optimal
Il est ici question de montrer que la ruée bancaire est
possible lorsque le contrat de dépôt est choisi pour
résoudre le problème de décision de la banque. Pour
maximiser l'utilité espérée, la banque doit choisir le
contrat de dépôt (c1*, c2*) satisfaisant la condition de premier
ordre suivante :
U' (c1 *) = RU' (c2 *)
Cette condition joue un rôle crucial pour
déterminer si la banque manquera de liquidité ou pas. Et si
l'aversion relative pour le risque est supérieure à 1, la
solution de la condition de premier ordre doit vérifier :
c1 >1

Cette condition implique qu'il existe la possibilité
d'une ruée. Si tous les déposants essaient de retirer à la
date 1, la demande totale de la consommation est c1* > 1. Or, le maximum qui
peut être fournie par la liquidation de tous les actifs longs est de 1.
Toutefois, il ne restera plus rien à la date 2, les déposants
vont se rejoindre à la ruée au lieu d'attendre jusqu'à la
date 2 pour retirer. Dans ce qui suit, le modèle suppose que les
préférences de l'agent doivent satisfait la condition que
· aversion relative pour le risque est supérieure
à 1, qui est,
> ? >
1, c 0
U»( c ) c
-
U' (c)
Afin de simplifier la caractérisation de
l'équilibre, le modèle ne considère que le cas particulier
dans lequel les actifs longs, une fois liquidés
prématurément, rapportent beaucoup plus que les actifs courts. En
d'autres termes :
· la valeur de liquidation de l'actif long est r = 1.
Cela implique que l'actif long domine l'actif court; le
modèle suppose ainsi dans ce qui suit que l'ensemble du portefeuille
bancaire est investi dans l'actif long.
Dans le cas d'une ruée bancaire, la valeur
liquidée du portefeuille de la banque est 1 unité du bien, de
telle manière que chaque consommation du déposant est aussi 1
unité de bien. Si la banque est solvable, les déposants
reçoivent le profil de consommation promise (c1, c2). Ces
quantités choisies pour maximiser l'utilité espérée
du consommateur typique dans le cas où la banque est solvable. Le
contrat de dépôt doit résoudre le problème de
décision suivant :
max ëU (c1) + (1 - ë) U(c2)
Rëc1 + (1 - ë) c2 = R
Pour comprendre la raison pour laquelle la contrainte
budgétaire prend cette forme, il faut noter que la banque a promis un
total de ëc1 unités aux consommateurs de type 1 qu'elle doit
liquider à la date 1. Le montant de l'actif long à gauche est de
(1 - ëc1) et cela rapporte R (1 - ëc1) d'unités de
consommation à la date 2. Ainsi, le montant maximum qui peut être
engagé aux épargnants (qui est de (1 - ë) c2) doit

20
être inférieur ou égal à R (1 -
ëc1). En effet, une unité de consommation à la date 1 est la
valeur R d'unités de consommation à la date 2.
f. Equilibre sans ruée
La banque peut éviter une ruée par le choix
d'un contrat sûr12 . En effet, les arguments en faveur de
l'existence d'un équilibre d'une ruée à la date 1 ont
été fondés sur l'hypothèse que c1> 1. Ainsi, si
tous les consommateurs rejoignent la ruée bancaire à la date 1,
il n'est pas possible que la banque puisse offrir à chacun c1. En fait,
la banque va procéder à la liquidation de tous ses actifs. En
outre, vu que les actifs de la banque sont épuisés à la
date 1, les personnes en attente jusqu'à la date 2 pour retirer ne
recevront rien. Afin de supprimer cette incitation à rejoindre la
ruée, la banque doit choisir un contrat de dépôt qui
satisfait la contrainte supplémentaire c1 = 1. Si on résout le
problème
max ëU(c1) + (1 -
ë)U(c2) s.t. Rëc1 + (1 -
ë)c2 = R c1 = 1
Le modèle trouve la solution (c1**, c2**) = (1, R).
Dans ce cas, la banque sera en mesure de donner à chacun le
remboursement promis c1 à la date 1. Plus précisément, si
1 - å des déposants retire nt à la date 1, la banque doit
liquider 1 - å unités des actifs longs, laissant å unit
és de ces actifs à pour les autres consommateurs. Ensuite, chaque
consommateur qui retire à la date 2 recevra åR / å = R>
1.
g. Caractérisation des régimes avec et
sans ruée
Si la banque s'attend à une ruée avec une
probabilité ð, la consommation du déposant est alors 1, quel
que soit son type. Avec une probabilité 1 - ð il n'y a pas de
ruée et avec une probabilité ë le déposant est de
type 1 et sa consommation est c1* et avec une probabilité 1-ë, il
est de type 2 et sa consommation c2*. Les résultats possibles sont
illustrés à la figure 3. L'utilité espérée
du déposant typique sera :
ð U 1 1 ð ë U c 1 ë
Uc 2 ,
( ) ( ) { ( 1 ) ( ) }
+ - + -
* *
12 Jusqu'à présent, le modèle a
supposé que la ruée se produit avec une probabilité ð
et que la banque prend cette possibilité comme étant donné
dans le choix d'un contrat de dépôt optimal

Le modèle nous a montré que le choix de
portefeuille de la banque (x, y) = (1, 0) et le contrat de dépôt
(c1*,2*) optimisera cet objectif, en prenant la ð probabilité d'un e
ruée comme donnée. Par ailleurs, si la banque choisit un contrat
de dépôt qui permet d'éviter tous les ruées,
l'utilité espérée du déposant typique est
ëU c 1 ë U c 1 ë
U 1 1 ë UR
( 1 ) ( ) ( ) ( ) ( ) ( )
** + - = + -
**
Le fait qu'il est préférable pour la banque
d'éviter la ruée ou d'accepter le risque d'une ruée avec
une probabilité ð dépend d'une comparaison entre les services
publics prévu dans chaque cas. Précisément, il sera
préférable d'éviter les runs si :
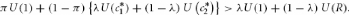
Maintenant, l'utilité espérée de la
stratégie de sécurité ëU (1) + (1 - ë) U (R) se
situe entre ces deux valeurs:
U (1) <ëU (1) + (1 - ë) U(R)
< + -
ë U c 1 ë U(c 2 )
( 1 ) ( )
* *
Figure 3. La détermination des zones qui
supportent les ruées
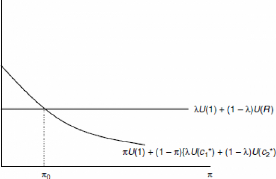
Source : Allen et Gale (2008)
Ainsi, il existe une valeur unique 0 <ð0 <1 tels que
:

22
ð U (1) (1 ð 0) ë U (
c ) (1 ë ) U ( c 2 )
ë U (1) (1 ë ) U ( R )
0 { }
+ - + - = + -
* *
1
Si ð = ð0, la banque va être indifférente
entre les deux stratégies. Evidemment, si ð <ð0 la banque va
préférer la ruée et ne préfère pas de
ruée si ð> ð0. Ces deux régions sont illustrées
dans la Figure 3. Le modèle nous avez montré que, tant que la
probabilité de ruée bancaire est suffisamment faible, il existe
un équilibre dans lequel la banque est prête à courir le
risque d'une ruée, parce que le coût d'éviter le
ruée est supérieur aux profits de la banque.
| 


