2.3 Le rapetissement de polygone
Dans cette section, nous appliquerons la théorie du
rapetissement de courbe aux SMA. Si on considère que les agents
représentent les sommets d'un polygone, en utilisant les
résultats du rapetissement de courbe euclidien, nous prouvons que ce
polygone va se rétrécir jusqu'à devenir un point qui n'est
autre que le centre des agents, et par ce fait réaliser la
stratégie de rendez-vous.
Nous commencerons par un aperçu mathématique sur
la géométrie euclidienne, le rapetissement de courbe, les
différentes propriétés des polygones, ensuite nous
étudierons deux méthodes mise en oeuvre par S. L. Smith [1] qui
appliquent le rapetissement de polygone au problème de rendez-vous, dont
Menger-Melnikov, et un autre schéma linéaire.
Considérons toujours le système
représenté ci-dessous, où les z sont les positions des
agents et
_zi leur vitesses respectives :
p
zi = xi + jyi i = 1, . . . , n j = -1
_zi = ui
où ui est calculé en fonction de la méthode
utilisée.
2.3.1 Préalables mathématiques
Dans ce qui suit, et pour pouvoir poursuivre, un aperçu
sur la géométrie euclidienne, la dynamique du rapetissement de
courbe qui en dérive, ainsi que quelques propriétés des
polygones.
Géométrie euclidienne
Définition 2.6 Une transformation euclidienne de
R2 est une fonction L : R2 . R2, L(x) = Ux+a.
Où U est une matrice orthogonale (2 x 2), a 2 R.
U est une matrice orthogonale == U~1 = UT
L'ensemble des transformations euclidiennes est l'ensemble de
toutes les rotations, translations, réflexions d'une figure dans
R2. Autrement dit, la géométrie euclidienne est
l'étude des propriétés des figures qui restent
inchangeables par des transformations euclidiennes. Ces
propriétés euclidiennes comprennent la distance, la courbure et
la colinéarité des points.
Rapetissement de courbe euclidien
Soit une famille de courbes lisses et fermées, x(p, t)
: [0, 1] x [0, r] - R2, situées dans un plan complexe
où p désigne les points le long de chaque courbe et t la famille
de courbe. La courbe initiale x(p, 0) évolue en fonction du temps
à x(p, r). Nous allons considérer dans un premier temps seulement
la première courbe noté x(p) = (x1(p), x2(p)).. Le vecteur
tangent à la courbe est donné pardx
dp = _x, son vecteur unité est T(p) = x_
k _xk = ( _x1(p); _x2(p))
k _xk .
et le vecteur unité de la normal qui est perpendiculaire
à la tangente (N(p) T(p) = 0) est : N(p) = (~ _x2(p)j
_x1(p))
k _xk .
Un nouveau paramètre de la courbe sera introduit pour les
prochains calculs "s" qui représente la longueur d'un arc, et ce afin de
décrire la distance autour de la courbe au lieu de p. Avec ds = k _xk
dp.
F 3 F 3
LT T L x' 1 x' 2
Soit la matrice de rotation A(s) = ] = ] où 0
décrit la différentielle par rapport
NT -x ' 2 x' 1
à "s". Pour calculer la dynamique du système,
nous allons d'abord calculer la dynamique des deux
vecteurs N et T pour obtenir l'équation de Frenet [12].
C'est à dire A'.
CHAPITRE 2. DIFFÉRENTES APPROCHES DE LA STRATÉGIE
DE RENDEZ-VOUS 31
A' = AGA~1A = C(s)A
Trouvons C(s)?
A-1 = AT = X0 --X2
001
(matrice orthogonale)
[ 0
X2X1

2
A' = 4
» »
X1 X2
--X »2 X » 1
3
5
2 3 2 3 2 3
» » 0 0 0 » 0 »C(s) = 1 = X1 X2
X1 --X2 = X1X1 + X2X2 X;X'2' -- X;i2 4 5
0 0 » 0 0
--X2 X1 X2 X1 --X1X2 -- X1X2 X1X1 +
X2X2
2 3
0
j 0 X1
posons : k(s) = X1X2 -- X1X2 = det 5=
det(X, ,X, ). Où k(s) est la courbure de la
courbe
X2 X2
X(s) et le rayon de courbure est : 1
1i(s)1-
Nous avons aussi :
(AAT)/ = A/AT + A(AT)/ = A/A-1 + (A-1)T(A/)T = A/A-1 +
(A/A-1)T
Avec : --(AAT )/ = 0, puisque : AAT = I.
--A/A-1 = C(s)
et donc : C(s) = --C(s).
[ 0 "
--X1X1 -- X2X2 --X1X2 + X1X2
» 0 0 » 0 » 0 »
X1X2
+
X1X2--X1X1
--
X2X2
--C(s) =

|
C(s) = --C(s) )
0 » 0 »
X1X1 + X2X2 = 0 D'où :
|
8
<
:
|
0 » 0 » 0 » 0 »
X1X1 + X2X2 = --X1X1 -- X2X2
0 » » 0 0 » » 0
X1X2 -- X1X2 = --X1X2 + X1X2
|
}
|
0 » 0 j ), i i ,
X1X1 + X2X2 = --(X1X1 + X2X2) )
|
C(s) =
[ 0 k(s)1
--k(s) 0 (2.19)
Retrouvons la dynamique du système :
dT
A(s) =[1 A/ (s) = [dd ds Ns1
A-1(s) = hT-1 N-1i
NT
d'après 2.19 :
|
2 AGA-1 = 4
dT
|
dT
ds
dN
ds
|
3hT-1 N-1i --k(s =[ 0 k(s)1
) 0
|
|
)
|
8
<
:
|
dTds N-1 = k(s)
dNds T-1 =
--k(s)
|
}
|
|
{
|
dTdsN-1N =
k(s)N
ddNs
T-1T = --k(s)T
|
}
|
)
|
8
<
:
|
dTds =
k(s)N
ddNs = --k(s)T
|
}
|
)L'équa-
|
|
|
|
|
2
)4
|
ds T-1 ds T-1
N-1
T
dN T-1 dN N-1 ds ' ds
|
1= [ 0 k(s)1
--k(s) 0
|
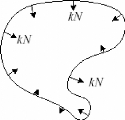
FIG. 2-5 - La dynamique du rapetissement de courbe
Dans la dynamique du rapetissement de courbe Euclidien, la courbe
x(p, t) est déformée le long de son vecteur normal N(p, t) avec
un taux proportionnel à sa courbure k(p, t). Et donc:
Dx
3p (p,t) = k(p,t)N(p,t) (2.20)
La formule 2.20 décrit la dynamique du rapetissement de
courbe Euclidien x(p, t) tel qu'il est montré dans la figure 2-5.
Rapetissement de polygone
Nous allons appliquer les résultats de Smith et autres
concernant le rapetissement de courbe aux systèmes multi-agents.
Considérons un groupe d'agents mobiles autonomes situés dans un
plan et formant les sommets d'un polygone à "n" cotés (voir la
figure 2-6). En créant un schéma de rapetissement de polygone
semblable à celui du rapetissement de courbe, les sommets (les agents)
convergeront à un point elliptique. Ainsi, la forme du polygone se
rétrécissant à un point aura les mêmes
propriétés que la théorie du rapetissement de courbe.
Avant, nous donnerons une définition formelle d'un n - gons ainsi que
quelques propriétés intéressantes.
Définition 2.7 Un n - gons est un circuit de "n"
segments de ligne : z1z2, z2z3,. . . , znz1,joignant chaque paire de
points consécutifs : z1, z2, . . . zn. Les segments sont
appelés cotés, et les points sommets.
Définition 2.8 Un polygone simple est un n - gons avec
les cotés non intersectés. Notons I3i les angles internes (dans
le sens contraire des aiguilles d'une montre) entre les côtés
consécutifs zizi+1 et zi_1zi d'un polygone. i = 1,.. . ,
n(modulo n). Ces angles satisfont :
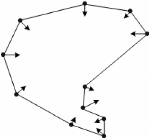
FIG. 2-6 - Rapetissement de polygone
Définition 2.9 Un n - gons convexe est n - gons simple
dont les angles internes satisfont : 0 ~ /3i ~ 7r,Vi=1,...,n.
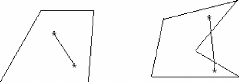
Polygone convexe Polygone concave
Une ligne tracée entre n'importe quels deux points
distincts du n-gons convexe appartient toujours à celui-ci.
| 


