Chapitre 2
Différentes approches de la stratégie
de rendez-vous
2.1 Introduction
Dans ce chapitre, nous étudierons plus en détail le
problème de rendez-vous, les différentes approches
adoptées par Smith [1] ainsi que les méthodes
associées.
Un schéma analytique du problème sera
présenté pour chaque méthode, vu qu'on utilise l'approche
de calcul numérique, par référence aux travaux de
Smith.
Dans le but de concevoir une stratégie de rendez-vous,
plusieurs méthodes suivant différentes approches ont
été étudiées dans la thèse de Smith, et ce
dans le but de trouver la méthode la plus efficace, la plus rapide et
aussi la moins coûteuse. Dans la première partie de ce chapitre,
nous expliquerons la première approche, qui est la poursuite cyclique et
dans la deuxième, le rapetissement de courbe appliqué au SMA.
2.2 La poursuite cyclique
Il a été montré dans la
littérature que le point de convergence d'un groupe d'agents et les
mouvements des agents mobiles autonomes peuvent être commandés en
employant des lois de poursuite cyclique (généralement
utilisée dans la commande de véhicules).
Smith et autres ont mis en place un modèle
mathématique décrivant cette stratégie comme suit : un
groupe d'agents représentés par des points de masses,
numérotés de 1 à n, la position de chaque agent peut
être décrite dans un plan complexe par le point z = x + jy , i =
1, ..., n, avec j = J--1
z = x + jy
CHAPITRE 2. DIFFÉRENTES APPROCHES DE LA STRATÉGIE
DE RENDEZ-VOUS 16
La stratégie est telle que l'agent « i » chasse
l'agent « i+1 ». La vitesse de l'agent « i » en direction
de l'agent « i+1 » est donnée par le modèle suivant
:
_zi =zi+1-zj, i=1,...,n-1
(2.1)
_zri = z1 - zri.
Suivant ce schéma, les agents vont converger à
leur centre stationnaire. Plusieurs stratégies peuvent être
inspirées de ce modèle de base, c'est ce que nous verrons dans
cette section. Mais avant, nous allons définir quelques concepts
mathématiques utiles à la suite du chapitre.
2.2.1 Préalables mathématiques
Pour continuer, nous avons besoin de définir quelques
concepts mathématiques utiles à la conception de notre
système, tels que les matrices circulantes, et circulantes par blocs, la
diagonalisation de matrices circulantes...
Matrices circulantes
Considérons un n-uplets (c1, C2, C3, ...,
cri) de nombres réels. La matrice circulante, est une matrice
carrée (n x n) dont les lignes sont composées du n-uplet
décalé à droite cycliquement modulo n. La forme
générale d'une telle matrice est la suivante :
|
6 6
6 Cri C1 C2 ~ ~ ~ Cri_1
6 6
C = 6 Cri_1 Cri C1 ~ ~ ~ Cri_2
|
(2.2)
|
|
...
2 C1 C2 C3 ~ ~ ~ Cri
|
...
|
...
|
..
.. ..
|
C2 C3 C4 ~ ~ ~ C1
D'une façon plus explicite, nous écrirons :
C =: circ(c1, C2, C3, ..., cri)
Définition 2.1 En algèbre linéaire, une
matrice carrée M d'ordre n (nEN*) à coefficients dans un corps
commutatif K, est dite diagonalisable si elle est semblable à une
matrice diagonale, c'est-à-dire s 'il existe une matrice inversible F
telle que F _1MF soit une matrice diagonale.
CHAPITRE 2. DIFFÉRENTES APPROCHES DE LA STRATÉGIE
DE RENDEZ-VOUS 17
C =cnP n1 + cn_1P n2 + ... + c2P + c1I (2.3)
avec:
010---0
001---0
P= =circ(0,1,0,...,0) (2.4)
... ... ... ... ...
100---0
Remarque 2.1 Ceci découle du fait que:
P2 =circ(0,0,1,0,..0,0), P3=circ(0,0,0,1,0,..,0),
...
Après certaines transformations sur la matrice C, nous
obtenons la formule . 3. Définition 2.2 posons :
qc(s) = cnsn_1 + cn_1sn~2 +
... + c2s + c1s°
d'où:
C = qc(P)
Pour le calcul des valeurs propres de C, que nous noterons VP(C),
nous devons d'abord calculer les valeurs propres de la matrice P. Davis [10] a
montré que :
VP(C) = {qc(.X) : 2 VP(P)}
Par définition de la matrice P dans [10] :
VP(P) =
{1,e2~jIn,e4~jIn,...,e2(n_1)~jIn}
(2.5)
Posons w = e2~iIn d'où:
VP(P) = {1,w,w2,...,wn_1}
= VP(C) = fqc(1);
qc(w); qc(w2); :::;
qc(wn~1)g
Après quelques calculs [1], nous obtenons la matrice
diagonale:
CHAPITRE 2. DIFFÉRENTES APPROCHES DE LA STRATÉGIE
DE RENDEZ-VOUS 18
qc(1) 0
·
·
· 0
A= 0 qc(w)
·
·
· 0
0
·
·
· 0
qc(wn-1)
C = FAF* avec F la matrice inversible de passage de la
forme :
1
F=
,Vn
1 1
·
·
· 1
1 w
·
·
· wn-1
. .
. .
. .
... ...
1 wn-1
·
·
·w(n-1)(n-1)
De cette manière, nous aurons montré que la matrice
circulante est diagonalisable.
Matrices circulantes par blocs
La matrice circulante par bloc est une matrice circulante
où chaque réel dans la matrice 2.2 est remplacé par une
matrice carrée Di (m x m), elle a la forme suivante :
2 D1 D2 D3
·
·
· Dn
6 6 6Dn D1 D2
·
·
· Dn-1
6
D =6 6Dn-1 Dn D1
·
·
·
Dn-2
D2 D3 D4
·
·
· D1
C'est une matrice de dimension (nm x nm), et elle peu aussi
être écrite en fonction de la matrice P(n x n) :
D= P n-1
0Dn+Pn-20Dn-1+
·
·
·+P0D2+I0D1
Définition 2.3 0 représente le produit de
kronecker.
Le produit de kronecker entre deux matrices A(n x m) et B est
définie comme suit :
a11B
·
·
· a1mB
an1B
·
·
· anmB
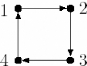
FIG. -1 - la structure d'une poursuite cyclique traditionnelle
à 4 agents
Les valeurs propres de A ® B sont données par tous
les produits possibles entre les valeurs propres de A et B.
| 

