2.2.2 Poursuite cyclique traditionnelle
C'est le cas le plus simple de la poursuite cyclique,
où chaque agent poursuit l'agent qui le suit dans l'ordre de
numérotation, tel qu'il est décrit dans le système 2.1. Ce
système peut aussi s'écrire dans la forme vectorielle suivante
:
z_ = A1z (2.6)
où A1 = circ(--1, 1,0, ..., 0). La matrice A1 = P -- I
où P est donnée par 2.4. Smith a démontré le
théorème suivant dans sa thèse [1] :
Théorème 2.1 Considérons la poursuite
cyclique dans le schéma . 6, pour toute configuration initiale, le
centre des agents z1(t), z2(t), ..., z,(t) est stationnaire et tous les zi(t),
(i = 1,..., n) convergent à ce centre.
Le centre des agents est donc stationnaire, et est donné
à chaque instant "t" par l'expression
1
n
z~ =
X,
i=1
suivante :
zi(t) (2.7)
Exemple 2.1 Prenons le cas de 4 agents, la poursuite cyclique est
représentée par le schéma -1, et la matrice de
transformation est :
--1 1 0 0
0 --1 1 0
A1=
0 0 --1 1
1 0 0 --1
2.2.3 Poursuite cyclique hiérarchique
Dans cette partie, le concept d'hiérarchie est
introduit et appliqué à la poursuite cyclique. La
hiérarchie veut dire une organisation des agents selon une
hiérarchie de groupes en plusieurs couches. Le cas le plus simple est le
schéma hiérarchique à deux couches, en suite nous
étudierons un schéma plus général avec un nombre de
couches quelconque.
Schéma hiérarchique à deux couches
Dans ce cas, les n agents de la poursuite cyclique
traditionnelle sont répartis en n2 groupes de tailles identiques, chaque
groupe contenant n1 agents (n1 x n2 = n). La stratégie est donc que, les
agents d'un groupe sont en poursuite cyclique (traditionnelle), et leurs
centres respectifs le sont aussi. Ceci veut dire que le centre de chaque groupe
d'agents poursuit le centre du groupe suivant dans l'ordre de
numérotation des groupes.
Chaque agent est caractérisé par sa position,
dans un plan complexe, notée zi,j où i (i = 1, :::,
n2) représente l'indice du groupe, et j (j = 1, ..., n1) l'indice de
l'agent dans le groupe "i". Le schéma décrivant cette
stratégie, et ainsi les vitesses de déplacement des agents est le
suivant :
|
8
|
_z1,1 = z1,2 -- z1,1 + d1,1
|
|
|
|
|
|
|
|
|
<>>>>>>
|
_z1,2
= z1,3 -- z1,2 + d1,2
|
|
|
|
groupe 1
|
>>>>>>:
|
}
|
|
(2.8)
|
|
|
...
|
|
|
|
|
|
|
|
|
|
_z1,n1
= z1,1 -- z1,n1 + d1,n1
|
|
|
|
...
|
|
|
|
|
|
8
|
_zn2,1 = zn2,2 -- zn2,1 + dn2,1
|
|
|
|
groupe 2
|
<>>>>> >
|
_zn2,2 = zn2 ,3 -- zn2 ,2 + dn2,2
|
}
|
|
|
|
...
|
|
|
|
>>>>>>:
|
|
|
|
|
|
_zn2,n1
= zn2,1 -- zn2,n1 + dn2,n1
|
|
|
Où les di,j sont les déplacements des
agents, la question est donc, : comment choisir ces déplacements pour
réaliser la stratégie décrite par 2.8
L'équation de déplacement des centres, sachant
qu'ils réalisent une poursuite cyclique, est :
:
zi = ~zi+1 -- zi, i = 1, ..., n2 -- 1 (2.9)
:
~zn2 = ~z1 -- ~zn2
CHAPITRE 2. DIFFÉRENTES APPROCHES DE LA STRATÉGIE
DE RENDEZ-VOUS 21
1
n1
~zi =
Xn 1
j=1
où le centre du groupe "i" est donné par:
zi;j (j = 1, ..., n1) (2.10)
1
n1
:
~zi =
Xn 1
j=1
en dérivant ce système, nous obtenons la vitesse de
déplacement du centre du groupe "i" :
di;j (j=1,...,n1) (2.11)
car, d'après 2.8 :
Xn 1 _zi,j = Xn 1 di;j Vi=
1,...,n2
j=1 j=1
d'après 2.11 et en remplaçant dans 2.9, nous
obtenons :
|
Xn 1
j=1
|
:
di;j = n1 ~zi= n1(~zi+1 -
~zi) (2.12)
|
|
Pn2
=
i=1
|
Pn1
j=1
|
di;j = n1
|
n2
P
i=1
|
:
~zi = 0
|
= le centre des n agents est stationnaire.
Plusieurs di;j peuvent être choisis satisfaisant
2.12, l'un des choix : di;j = zi+1,j - zi,j.
Ceci veut dire que l'agent "j" dans le groupe "i" poursuit
l'agent "j" dans le groupe "i+1". Si on remplace les di;j par leurs
expressions dans 2.8, nous obtenons la dynamique de l'agent "j" du groupe "i"
:
_zi;j = zi,j+1 - zi;j + zi+1,j -
zi;j (2.13)
nous remarquons que l'agent "j" du groupe "i" a un lien avec
l'agent "j+1" du même groupe, et un lien avec l'agent "j" du groupe "i+
1". D'où chaque agent aura besoin de deux liens de communication
(capteurs). Avec cette stratégie, le système comporte 2n
senseurs.
L'équation 2.13 s'écrit dans une forme vectorielle
:
z_=Bz+Dz
où B est la matrice diagonale par blocs
représentant la poursuite cyclique à l'intérieur d'un
groupe.
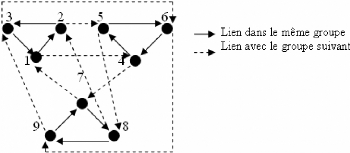
FIG. 2-2 - Structure d'un schéma hiérarchique
à 2 couches (9 agents, 3 groupes)
avec A1 = (P - I)(n 1Xn1) telle qu'elle est définie dans
la poursuite cyclique traditionnelle. La matrice D représente les
di;j et est donc de la forme :
D = circ(-1,1,0,...,0)(n2Xn2)®In1
= (P - I)(n2xn2) ® In1 = circ(-I, I,0,... , 0)
où In1 = S représente les connexions de chaque
agent dans un groupe aux agents du groupe suivant.
Un "1" dans la fg~emeposition de la matrice S (f,g =
1, ...,n1) indique que le f~eme agent dans un groupe détecte
le g~eme agent du groupe suivant (modulo n2).
posons A2 = B+D = circ(A1 -I, I,0, ..., 0), où A2 est une
matrice circulante à blocs de dimension (n x n) où chaque bloc
est de dimension (n1 x n1).
le système devient alors :
z_ =A2z
Exemple 2.2 Considérons un groupe de 9(n) agents, et un
schéma hiérarchique à deux couches, avec 3(n2) groupes de
3(n1) agents (voir figure 2-2). La matrice de transformation est donc :
|
2
-1 1 0
6
6
A2 = circ(A1 - I,I,0,...,0) avec A1 = 6 0 -1 1
4
1 0 -1
A2 = circ(-2, 1,0, 1,0,0,0,0,0).
|
= circ(-1, 1,0). et I =
|
100
010
001
|
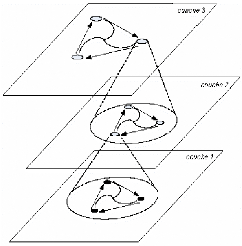
FIG. 2-3 - Trois couches d'hiérarchie dans une poursuite
cyclique
Schéma général
Dans un schéma plus général, nous avons L
couches d'hiérarchie. La première couche contient n1 agents, la
deuxième contient n2 sous-groupes de n1 agents, la troisième n3
groupes de n2 sous- groupes de n1 agents, ... (voir Figure 2-3)au total, nous
avons r'L nm = NL.
m=1
Le système est le suivant :
z_=ALz (2.14)
où z est un vecteur colonne de taille NL (le nombre
d'agents global), et AL est une matrice de dimension (NL x NL). Pour L = 1, la
matrice A1 = (P - I)n1~n1:
A chaque fois que nous ajoutons une couche, nous devons nous
assurer que le comportement de la couche inférieure reste stable. Ceci
veut dire que les agents / les groupes de la couche inférieure restent
en poursuite cyclique. Des senseurs sont ajoutés entre les centres des
groupes d'une même hiérarchie, pour qu'ils réalisent une
poursuite cyclique au niveau supérieur. Comme pour le schéma
hiérarchique :
- Les A1 au long de la diagonale représentent la poursuite
cyclique dans chaque groupe.
- Les "-I" au long de la diagonale, associés aux "I" au
long des blocs qui suivent, représentent les connexions entre les
groupes pour créer la nouvelle couche d'hiérarchie.
Chaque agent dans un groupe prend la position de l'agent dans le
groupe suivant moins sa propre
position, pour créer la nouvelle hiérarchie. Une
hiérarchie à L couches est décrite par le système
2.14 où, la matrice AL est obtenue de façon récursive
à partir de A1, de la façon suivante:
A1 = circ(-1,1,0,...,0) (2.15)
Am = circ(Am_1 - I,I,0, ..., 0) m = 2, ..., L
où Am est une matrice composée de
nm blocs de dimension Nm_1 X Nm_1.
Le nombre de liens de communication:
Nous remarquons que, pour mettre en place chaque nouvelle
couche, tout agent doit avoir un lien avec un agent d'un autre groupe, ceci est
décrit par la deuxième diagonale "I" dans 2.15. D'où
chaque agent aura L liens de communication avec les autres agents. Ainsi, le
système compte un total de LNL liens.
La question qui se pose naturellement est comment choisir la
distribution d'agents qui donne le meilleur taux de convergence (que nous
calculerons dans la dernière partie de cette section)? Smith [1] a
introduit et démontré le théorème suivant :
Théorème 2.2 Dans le cas où /NL est un
entier, la distribution uniforme des nm :
pn1 = n2 = ~ ~ ~ = nL = NL (2.16)
est une distribution optimale. De plus elle est la seule à
l'être. Sachant que la distribution optimale, qui satisfait
r'L nm = NL, est celle qui donne le taux de convergence
le plus important.
m=1
Remarque 2.2 Cette solution donne une augmentation dans le taux
de convergence équivalente à
RL = N2(n_1)' L
L que nous verrons ensuite comment calculer.
Remarque 2.3 Quand pNL n'est pas un entier, il peut exister
plusieurs distributions optimales.
Par exemple, pour NL = 12, L = 2, deux
solutions optimales : {n1, n2} = {3, 4} et {n1, n2} = {4, 3}.
| 


