La norme française définit la classification des
granulats d'après les dimensions de leurs grains exprimées en
ouvertures de tamis à mailles carrées en millimètres
(Jeuffroy, G. ; Sauterey, R., 1991).
· d/D s'il satisfait aux conditions suivantes :
Refus sur le tamis de maille D et tamisât au tamis de
maille d, compris :
- entre 1 et 15 % si D > 1,58d,
- entre 1 et 20 % si D = 1,58d.
Refus nul sur le tamis de maille 1,58D, tamisât au tamis
de maille 0,63d < 3 %, d étant = 0,5mm.
· 0/D s'il satisfait aux conditions suivantes :
Refus sur le tamis de maille D compris entre 1 et 15 %,
Refus nul sur le tamis de maille 1,58D.
Il existe six classes granulaires principales
caractérisées par les dimensions extrêmes d et D des
granulats rencontrés (Dupain ; Lanchon ; Arroman, St., 2004) :
- les fillers 0/D avec D < 2 mm et au moins 70 % de passant
à 0,063 mm,
- les sablons 0/D avec D = 1 mm, et moins de 70 % de passant
à 0,063 mm ; - les sables 0/D avec 1 < D = 6,3 mm ;
- les graves 0/D avec D > 6,3 mm ;
- les gravillons d/D avec d = 1 mm et D = 125mm ;
- les ballasts d/D avec d = 25 mm et D = 50 mm.
La norme française distingue deux types de Graves Non
Traitées (GNT), selon leur mode d'élaboration (Jeuffroy, G. ;
Sauterey, R., 1991) :
- GNT type A obtenue en une seule fraction (tout-venant)
directement sur une installation de criblage et de concassage, permettant
d'obtenir une compacité minimale à l'OPM de 80 %,
- GNT type B obtenue par mélange de deux (ou plusieurs)
fractions granulométriques différentes. Elles sont
malaxées et humidifiées en centrale, permettant d'obtenir une
compacité minimale à l'OPM de 80 % pour la catégorie B1 et
82 % pour la catégorie B2. Ce type de GNT permet d'obtenir une meilleure
qualité de mise en oeuvre.
3. - Les fuseaux granulométriques
Bien qu'elles soient appliquées dans ce paragraphe
à la granulométrie, elles doivent être
étendues
à l'ensemble des propriétés des granulats (Equivalent de
sables, etc.). Le fuseau
granulométrique est la zone délimitée par
deux courbes granulométriques enveloppes (Jeuffroy, G. ; Sauterey, R.,
1991). On distingue :
- Le fuseau de spécification propre à la technique
considérée, qui définit la zone dans laquelle doivent se
situer les fuseaux de tolérance,
- Le fuseau de fabrication, qui contient 95 % des courbes
granulométriques du matériau fabriqué. Un fuseau de
fabrication est entièrement inclus dans le fuseau de
régularité. Sa définition requière au moins 15
valeurs afin d'être suffisamment représentatif et est
établit par le producteur de granulats ;
- le fuseau de régularité, ou de tolérance,
qui définit l'étendue de la zone dans laquelle doivent se situer
95 % des courbes obtenues au cours du contrôle.
4. - Les différentes approches pour
l'étude des matériaux non liés
En fonction de l'échelle d'observation, il y a
différentes approches qui peuvent être adoptées pour la
détermination et l'étude des caractéristiques des
matériaux de chaussées (Gidel, 2001 ; Habiballah, 2005).
4.1. - L'approche microscopique
L'observation pour cette approche se fait à
l'échelle des granulats. On observe les caractéristiques
géométriques et mécaniques des grains.
Les observations à relever à l'échelle
granulaire afin de déterminer les caractéristiques de la grave
non traitée sont les suivantes :
- Les caractéristiques liées à la
géométrie globale des grains : la granularité, la taille
des grains et leur forme, l'angularité et la rugosité.
- Les caractéristiques mécaniques des grains
sont évaluées selon leurs duretés et leurs
résistances. La dureté des granulats est un facteur à
prendre en compte dans la classification des matériaux non liés
des chaussées souples. En absence de liant, les granulats sont
amenés à supporter plus d'efforts d'attrition et de
fragmentation. La résistance à ce genre d'agression repose sur la
nature minéralogique des granulats. Cette résistance est
mesurée par l'essai Los Angles (LA) et par l'essai Micro-Deval (MDE).
4.2. - L'approche macroscopique
L'échelle de l'observation est celle d'un
échantillon homogène dont les dimensions sont suffisamment
supérieures au diamètre maximal des grains afin de pouvoir
assimiler l'échantillon à un milieu continu. Grâce à
cette approche, il est facile de simuler des sollicitations et de relever les
réponses de l'échantillon. Cette approche est l'une des bases des
méthodes de dimensionnement rationnel des chaussées. Parmi les
essais utilisés, il y a l'essai CBR (Californian Bearing Ratio) et
l'essai triaxial à chargements répétés (TCR).
4.3. - L'approche globale
Pour cette approche, l'observation des
phénomènes se fait à l'échelle des couches. Elle
permet l'étude du comportement de l'ensemble d'une structure de
chaussée en prenant en compte les conditions in situ non
réalisables dans les deux premières approches. Dans le cas des
chaussées souples, l'approche globale de l'étude du comportement
mécanique des matériaux à l'échelle des couches est
basée sur la mesure de la déformation verticale en surface de la
chaussée. La méthode réglementaire consiste en une
évaluation globale de l'état de la structure et du sol support
à partir de la comparaison de la déflexion mesurée avec
des seuils prédéfinis (exemple de la structuration du code de
calcul Alizé 3). L'approche globale s'appuie sur des essais
réalisés sur l'ensemble chaussée-sol support, notamment
l'essai de
plaque statique et cyclique, la dynaplaque, le manège de
fatigue et les chaussées instrumentées.
5. - Caractéristiques géométriques
des granulats routiers
Les matériaux constituant les différentes
couches d'une chaussée peuvent être des matériaux
concassés ou roulés. Cependant, afin de disposer d'un angle de
frottement le plus fort possible, il est nécessaire d'exiger un indice
de concassage d'autant plus élevé que le trafic est plus
important et la charge légale à l'essieu plus lourde.
Les caractéristiques géométriques
principales des granulats routiers sont : l'état de surface,
l'angularité, la forme et la granularité (Tourenq ; Denis,
1982 in Gaye, 1995).
5.1. - Etat de surface des granulats
Dans le cas des roches polycristallines (Ø > 1 mm), la
rugosité dépend de la structure de la roche. Si le grain est
monominéral (Ø < 1 mm), la surface est
généralement lisse.
Pour les roches polycristallines, la rugosité
dépend de la dimension « d » des cristaux. Plus une roche a un
« grain fin », plus sa cassure est lisse. Par contre, les roches
à « gros grain » ont toujours des surfaces rugueuses.
L'état de surface des grains joue un rôle au
niveau de la maniabilité des matériaux, de la stabilité
des assises non traitées et de la microrugosité des couches de
surface. Cependant, l'action du trafic tend à polir la surface des
grains, mais il est admis qu'une bonne microrugosité assure
généralement une bonne adhérence à faible
vitesse.
5.2. - Angularité des granulats
Elle joue un rôle important pour les gravillons de la
couche de roulement, en améliorant l'adhérence, et pour ceux des
assises de chaussées, dont elle améliore la stabilité.
Pour un granulat concassé de roche massive, elle est
égale à 100 %.
Pour un granulat d'origine alluvionnaire, elle est définie
par deux données :
- l'indice de concassage IC, proportion en poids
d'éléments supérieurs à la dimension D du
granulat élaboré,
- le rapport de concassage RC, rapport entre d
du matériau soumis au concassage et D du granulat
obtenu.
Pour les assises de chaussées non traitées,
l'angularité favorise les propriétés mécaniques en
augmentant l'angle de frottement interne : celui-ci augmente d'environ 12°
dans un essai triaxial quand on passe des billes de verre entièrement
roulées aux billes de verre concassées. Pour les couches de
roulement, ce facteur favorise l'adhérence pneumatique, la rupture du
film d'eau et le drainage.
La maniabilité et la compactibilité sont
également liées à l'angularité : le
déplacement relatif des grains et leur mise en place sont
facilités lorsqu'ils sont arrondis.
5.3. - La forme des granulats
Elle joue un rôle important à la fois pour les
granulats de la couche de roulement, des gravillons plats ayant tendance
à se coucher au moment du compactage, et pour les matériaux
d'assise, des granulats plats ou allongés réduisant la
compacité et la stabilité.
Elle a aussi une grande influence sur les
caractéristiques mécaniques des matériaux (Los Angeles,
Micro-Deval, fragmentation dynamique).
10

Tableau 1. - Formes des granulats.
5.4. - La granularité des granulats
Elle caractérise la répartition du granulat en
tranches dimensionnelles. La granularité a une importance primordiale
car elle permet d'obtenir une compacité maximale et d'éviter la
ségrégation au moment de la mise en oeuvre.
La granularité que l'on peut maîtriser et
optimiser pour tous les matériaux, apparaît comme le recours le
plus général pour corriger les autres caractéristiques
géométriques des granulats et dans une certaine mesure une
résistance mécanique déficiente.
6. - Le Compactage des matériaux
6.1. - Définition
Compacter un matériau, c'est réduire le volume
des vides de ce matériau et organiser la structure des grains de
manière à obtenir un assemblage plus stable. Cette
opération qui s'appelle le compactage peut être obtenue par des
sollicitations statiques (compactage statique), dynamiques (compactage
dynamique), ou par vibrations (compactage in situ) (Kabre, 1991
in Gaye, 1995).
6.2. - Rôle du compactage sur la durée de
vie des ouvrages
Le compactage met le matériau dans un état
suffisamment serré de telle sorte qu'un tassement ultérieur soit
impossible ou peu important. Les mouvements relatifs sont réduits ou
supprimés, diminuant ainsi l'attrition. En réduisant le volume
des vides, le compactage augmente la densité apparente sèche et
diminue la perméabilité qui est fonction de l'indice des
vides.
Le compactage entraîne une élévation des
caractéristiques mécaniques. En effet, le resserrement des grains
augmente le nombre de contacts entre eux et par conséquent leur
frottement. L'angle de frottement interne et la cohésion en sont accrus.
Il y a également augmentation considérable du module de
déformation.
6.3. - Les paramètres influents du
compactage
o La teneur en eau
L'influence de la teneur en eau et de l'énergie de
compactage sur la densité sèche du matériau a
été mise en évidence en 1933 par l'ingénieur
américain Proctor (Tchouani Nana, J.M. ; Callaud, M., 2004).
En effet pour une énergie de compactage donnée,
si l'on fait varier la teneur en eau w et l'on
représente graphiquement la variation du poids
volumique sec ãd en fonction de cette teneur en eau, on obtient une
courbe en cloche qui présente un maximum appelé Optimum Proctor
séparant de gauche à droite la branche sèche et la branche
humide.
Lorsque la teneur en eau est raisonnable, l'eau joue un
rôle de lubrifiant et la densité sèche
augmente avec la
teneur en eau jusqu'à un maximum (branche sèche). Par contre
lorsque la
teneur en eau est élevée (branche humide), l'eau
absorbe une partie importante de l'énergie de compactage. Elle occupe la
place des grains solides et aucun tassement n'est possible.
o La nature du matériau
Le comportement et les sollicitations
développés par les matériaux sont plus ou moins fonction
de leur nature. De façon générale, la courbe Proctor est
très aplatie pour les sables et par contre présente un maximum
très marqué pour les argiles plastiques (Tchouani Nana, J.M. ;
Callaud, M., 2004).
Pour les matériaux à courbe Proctor aplatie, le
compactage est peu influencé par la teneur en eau. Ces matériaux
sont peu sensibles à l'eau mais il est souvent difficile
d'améliorer leurs caractéristiques (énergie de compactage
à fournir plus importante).
o L'énergie de compactage
Pour un matériau donné, si l'énergie de
compactage augmente, le poids volumique maximum augmente et les courbes
deviennent plus pointues.
Khaye ; Machet ; Morel (1979) in Gaye (1995) montrent
que la densité sèche après compactage augmente avec la
charge de la roue et la pression de gonflage.
Martinez (1980) in Gaye (1995) remarque que la
réponse des matériaux granulaires aux sollicitations cycliques
qui n'atteignent pas les charges de rupture peut être de trois types :
- Adaptation : l'énergie dissipée et la
déformation permanente sont nulles. La réponse
du matériau est réversible et élastique,
- Accommodation : les déformations permanentes sont
stabilisées et l'énergie dissipée
n'est pas nulle (phénomène
d'hystérésis). La réponse réversible est non
linéaire ;
- Rochet : l'énergie dissipée et les
déformations permanentes augmentent avec la
sollicitation jusqu'à la stabilisation ou la rupture
(déformation plastique).
o L'angularité, la forme, la granularité
et le pourcentage des fines
Des matériaux très anguleux se mettent
difficilement en place entraînant l'augmentation de l'énergie de
compactage.
Arquie ; Morel (1988) in Gaye (1995) montrent qu'un
matériau ayant une bonne granularité aura une densité
maximale plus élevée qu'un matériau creux ou ayant un
excès de sable. Kabre (1991) in Gaye (1995) indique que la
compacité augmente avec le coefficient
d'uniformité
CU = D 60
.
D10
D60 et D10 sont les
diamètres des tamis qui laissent passer respectivement 60 % et 10 %
du
matériau.
Machet et Morel (1980) in Gaye (1995) trouvent
que pour une énergie de compactage donnée, l'indice des vides
décroît avec le pourcentage d'éléments fins (<
80um).
o Le sol-support
Pour une même épaisseur de matériau, un
support plus rigide conduit à des densités plus
élevées. Les sollicitations développées par un
rouleau vibrant sont considérablement influencées par les
caractéristiques du sol-support.
7. - Dimensionnement des structures de
chaussées
Le sol ne peut seul supporter un trafic routier sans subir
d'importantes déformations. C'est pourquoi il est surmonté d'un
corps de chaussée dont le rôle principal est la répartition
latérale des contraintes dues à des charges roulantes en surface
afin de les amener à des niveaux compatibles avec les
caractéristiques mécaniques du sol naturel.
12
La structure de la chaussée est constituée du bas
vers le haut de la Plate-forme (éventuellement surmontée d'une
couche de forme), de l'assise et de la couche de surface.
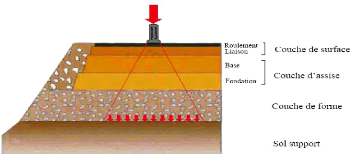
Fig. 1. - Structure de chaussée type et
répartition des contraintes (LCPC-SETRA, 1994)
La plate-forme constitue le support sur lequel repose la
chaussée. Elle est constituée du sol support (déblai ou
remblai) désigné dans sa zone supérieure (sur 1m
d'épaisseur environ), par le terme Partie Supérieure des
Terrassements (PST), et dont la surface constitue l'arase de terrassement ; et
d'une couche de forme éventuelle (LCPC-SETRA, 1992).
L'assise est généralement constituée de
deux couches, la couche de fondation surmontée de la couche de base. Ces
couches apportent à la chaussée la résistance
mécanique aux charges verticales induites par le trafic. Elles
répartissent les pressions sur la plate-forme afin de maintenir les
déformations à ce niveau dans des limites admissibles.
Eventuellement on peut trouver, entre la plate-forme et la
fondation une sous-couche.
La couche de surface est la couche supérieure de la
chaussée. Elle est constituée de la couche de roulement sur
laquelle s'exercent directement les agressions conjuguées du trafic et
du climat, et le cas échéant, d'une couche de liaison,
intermédiaire entre les couches d'assise et la couche de roulement qui
permet d'assurer une bonne adhérence entre la couche de base et la
couche de roulement.
7.1. - Les modèles empiriques et semi empiriques
de dimensionnement
Ces modèles sont fondés sur une observation
expérimentale des chaussées et de leur comportement sous trafic.
Il existe plusieurs méthodes empiriques et semi empiriques parmi
lesquelles nous avons l'habitude de citer la méthode du CBR et celle du
CEBTP.
7.1.1. - La méthode du CBR
Elle est basée d'une part sur la résistance au
poinçonnement du sol de fondation, résistance
appréciée par un essai normalisé, l'essai CBR, et d'autre
part sur la théorie de Boussinesq donnant la répartition en
profondeur des pressions verticales (Fall, M., 1993).
On considère un massif homogène, isotrope et
élastique limité par un plan horizontal et de dimension infinie.
Si l'on applique à la partie supérieure du massif une charge
verticale P répartie uniformément sur un cercle de rayon R, il en
résulte sur un plan horizontal situé à une profondeur z,
une pression verticale óz.
A la profondeur z = e correspondant par exemple à
l'épaisseur de la chaussée, la pression óe qui
s'exerce sur le sol de fondation doit être inférieure à la
résistance au poinçonnement I de ce sol.
óe = KI (K coefficient de
sécurité tenant compte du caractère empirique de
l'essai).
Ceci a permis d'établir des abaques donnant, en fonction
du CBR, l'épaisseur nécessaire du corps de chaussée.
13
7.1.2. - La méthode proposée par le CEBTP
pour les pays tropicaux
Cette méthode s'appuie sur les principes de bases suivants
:
- Dans le cas des chaussées souples, l'indice portant
de la plate-forme et l'intensité du trafic (Tableau 2)
déterminent l'épaisseur totale de la chaussée
(BCEOM-CEBTP, 1975),
- Dans le cas des chaussées à assise
traitée donc susceptibles d'une rupture en traction, le dimensionnement
précédent doit être complété par une analyse
théorique pour s'assurer que les contraintes de traction à la
base des couches rigidifiées sont compatibles avec les performances des
matériaux (BCEOM-CEBTP, 1975).



