I. Introduction
L'analyse des séries temporelle est un champ
d'étude en perpétuelle évolution ces dernières
années. D'énormes progrès ont été
réalisés dans diverses disciplines, notamment en économie,
finance,....En effet Wold (1938) est à la base du développement
qu'a connu la classe des modèles autorégressifs moyennes mobiles
(ARMA) univariés.
Cependant, les statisticiens George Box et Gwilym Jenkins ont
contribué dans les années 70, à populariser la
théorie des séries temporelles univariées par leur
célèbre ouvrage. La modélisation univariée de Box
& Jenkins concerne les processus ARMA (p, q), ARIMA(p, d,
q) ou SARIMA(p, d, q)(P, D ,Q). Ces auteurs rassemblent tous les
travaux dans une méthodologie itérative. Cette dernière
englobe trois étapes essentielles à savoir : l'identification du
modèle, l'estimation du paramètre et la validation à
travers des tests. Une fois le modèle déterminé, nous
pouvons faire des prévisions.
La première étape consiste à identifier le
modèle qui pourrait engendrer la série. Elle consiste, d'abord
à transformer la série afin de la rendre stationnaire. Le nombre
de différentiations détermine l'ordre d'intégration d.
Ensuite il s'agit d'identifier le modèle ARMA (p, q) de la
série transformée avec l'aide du corrélogramme simple et
du corrélogramme partiel. Le graphique des coefficients
d'autocorrélation simple (corrélogramme simple) et
d'autocorrélation partielle (corrélogramme partiel) donnent une
information sur l'ordre du modèle ARMA. Après avoir
choisi un ou plusieurs modèles ARMA théoriques, il faut
estimer leurs paramètres en utilisant une méthode non
linéaire (moindres carrés non linéaires ou maximum de
vraisemblance). Ces méthodes sont appliquées en utilisant les
degrés (p, d, q) et (P, D, Q) trouvés dans
l'étape d'identification. Une fois les coefficients estimés, il
s'agit de vérifier l'adéquation du modèle aux
observations. Il existe plusieurs tests : tests graphiques de
l'autocorrélation des résidus, test de Box-Ljung, et d'autres
tests qui confirment la blancheur des résidus. Enfin,
l'intérêt de l'approche de Box-Jenkins est qu'une
modélisation ARMA conduit à des prévisions
optimales si la variance de l'erreur de prévision est minimale. Cette
approche se schématise comme suit :
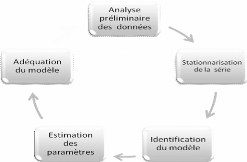
Organigramme de la méthode de Box et
Jenkins
31
II. Démarche de la méthode de Box et
Jenkins
II.1. Analyse préliminaire
L'analyse préliminaire est une phase non
coûteuse, elle permet avant tout test ou traitement
statistique
approprié, d'observer la représentation graphique de la
série (les observations du
processus {Xt , tE cents } en fonction du
temps).
En effet, parfois une simple visualisation du graphe permet de
détecter ou soupçonner l'existence de plusieurs composantes
(tendance, saisonnalité,...) donc il faut, bien évidemment,
confirmer ou infirmer l'existence par des tests appropriés.
Cette étape, permet aussi de prendre des options sur les
variables, tels que : corriger les données aberrantes, suppléer
celles manquantes ou effectuer des transformations...etc.
II.2. Stationnariser la série
Les résultats de l'analyse des séries
chronologiques reposent sur l'hypothèse de stationnarité du
second ordre, mais souvent les caractéristiques stochastiques d'une
série (moyenne, variance) se trouvent modifiées dans le temps,
c'est le cas par exemple lorsque :
- On constate que la série est saisonnière par
l'apparition des pics marquants de périodicité S dans la fonction
d'autocorrélation simple ou dans la représentation graphique de
la série.
- La chronique est affectée d'une tendance, dont il
convient de déterminer la nature par les tests cités de
Dickey-Fuller (voir chapitre 1).
II.3. L'identification du modèle
adéquat
Cette étape consiste à identifier le modèle
ARMA susceptible de représenter la série, c'est pour
cela qu'il est important de se familiariser avec les données en
examinant le graphe de la série chronologique (présence de
saisonnalité, stationnarité,...) qui permet de faire une analyse
préliminaire qui consiste par exemple à corriger les
données aberrantes, transformer les données (transformation
logarithmique, inverse, racine carrée,...) puisqu'il faut se ramener
à un modèle ARMA stationnaire, le recours aux
différences premières ordinaires, différences
premières saisonnières, différences ordinaires et
saisonnières. Le choix est dicté par l'allure graphique de la
série. D'ailleurs le choix de la transformation des données est
plus facile après avoir appliqué les opérateurs de
différence adéquats. Il est conseillé de comparer les
variances des différentes séries. La série avec la plus
petite variance conduit souvent à la modélisation la plus simple.
Ainsi un examen du corrélogramme s'impose. Cette phase est la plus
importante et la plus difficile, elle consiste à déterminer,
parmi l'ensemble des modèles ARMA(p,q), le modèle le plus
représentatif du phénomène
étudié, elle est fondée sur l'étude des
corrélogrammes: simple et partiel; l'idée de base est que chaque
modèle ARMA possède des fonctions d'autocorrélation
(simple et partielle) théoriques spécifiques, le statisticien
essaie donc, à l'aide de son expertise, de reconnaître et
d'identifier, en comparant l'éventuelle similitude de ces fonctions
théoriques et estimées. Il peut alors choisir un ou plusieurs
modèles théoriques (en général, le choix porte sur
trois modèles au plus) en se basant sur les propriétés
suivantes :
? Si le corrélogramme simple n'a que ses q premiers
termes différents de zéro et que les termes du
corrélogramme partiel diminuent exponentiellement vers zéro ou
d'une manière sinusoïdale amortie, nous pouvons pronostiquer un
moyenne mobile d'ordre q : MA (q).
? Si le corrélogramme partiel n'a que ses p premiers
termes différents de zéro et que les termes du
corrélogramme simple diminuent exponentiellement vers zéro ou
d'une manière sinusoïdale amortie, nous identifions un
autorégressif d'ordre p : AR (p).
? Si les fonctions d'autocorrélation simple et partiel
n'apparaissent pas tronquées, il s'agit d'un processus ARMA ; en fait
dans ce cas il est très difficile d'identifier directement les vrais
paramètres du modèle, il convient donc d'en proposer plusieurs
pour éliminer, après des tests appropriés, ceux qui ne
reflètent pas les variations du processus.
II.3 Estimation des paramètres du
modèle
Une fois l'étape de l'identification terminée, il
faut estimer les paramètres qui sont les coefficients des
polynômes AR et MA ainsi que les polynômes
saisonniers SAR et SMA, et la variance des résidus
2
cr .
La méthode d'estimation la plus couramment utilisée
est celle du maximum de vraisemblance ou bien la méthode des moindres
carrés. Plus spécifiquement la technique consiste à
construire une fonction appelée fonction de vraisemblance et à
maximiser son logarithme par rapport aux paramètres I
i et Oj (avec i := 1,.., p et j :=
1,..., q) permettant de trouver la valeur numérique la
plus vraisemblable pour ces paramètres. L'étape
d'estimation achevée, l'étape suivante va nous permettre de
valider le(s) modèle(s) estimé(s).
II.4 Validation
A l'étape de l'identification, les incertitudes
liées aux méthodes employées font que plusieurs
modèles en général sont estimés et c'est l'ensemble
de ces modèles qui subit alors l'épreuve des tests, il en existe
de très nombreux critères permettant de comparer les performances
entre
modèles; nous pouvons citer les tests sur les
paramètres et les tests sur les résidus. II.4.1 Tests
concernant les paramètres
Tous les coefficients du modèle retenu doivent être
significativement différents de zéro, il convient donc d'utiliser
le test de Student classique.
· Test de Student sur les
paramètres
Il s'agit dans cette étape de tester la
significativité des paramètres m i et
Oj (i=1 ... ,p et j =
1... ,q) dans la formulation obtenue. Nous rejetterons avec un
risque 5% l'hypothèse que le paramètre est nul si :
à
> =
t a t a
( 1,9 6)
(Même procédure pour les Oj).
m
i
( )
m i
à
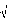
Var
II.4.2 Tests sur les résidus
Le processus estimé est évidemment de bonne
qualité si la chronique calculée suit les évolutions de la
chronique empirique. Les résidus entre les valeurs observées et
les valeurs calculées par le
modèle, doivent se comporter comme un bruit blanc. Pour
montrer que les { Et , t E cents } forment
un bruit blanc, nous devons vérifier si :
-La moyenne des résidus est nulle, sinon il convient
d'ajouter une constante au modèle.
-Le graphe des résidus en fonction du temps semble
approximativement compatible avec une suite de variables aléatoires non
corrélées. C'est ainsi que nous proposerons une multitude de
tests concernant les caractéristiques du résidu
souhaité.
è Test de Box-Ljung
Lorsque le processus est bien estimé, les résidus
entre les valeurs observées et les valeurs estimées par le
modèle doivent se comporter comme un bruit blanc. Nous noterons par la
suite Eàt le résidu d'estimation du
modèle.
o Principe du test
Ce test permet de savoir si les résidus forment un bruit
blanc ou non, pour le réaliser : nous observons le corrélogramme
des erreurs du modèle optimal, si tous les pics sont dans la bande de
confiance de plus la probabilité de significativité est
supérieure à 0.05 alors les résidus forment un bruit
blanc.
Pour confirmer ce résultat nous testons
H0 : « Les autocorrélations au
pas K, (k=N/5) sont non corrélés » C'est-à-dire
H0 : « p1 =p2
=...=pK = 0 » Contre H1 : «
3p j : j=1,k tel que pj ~0
».
= +
( )?= -
2 p 6 Statistique de BOX-LJUNG au pas K avec
:
K 2 ( )
Q n n i
n i
i 1
K : nombre de retard choisi. N : Taille de
la série brute. n : nombre de résidus.
o Règle de décision Si
Q <2 ? K - p - q - P
- Q)
? , degrés de liberté nous acceptons
l'hypothèse H0 que les résidus
sont non corrélés, Sinon les résidus ne
forment pas un bruit blanc et le modèle est inadéquat.
è Test des Points de
Retournements
Nous dirons que la suite des données 6
1 , 6 2 , ,6n
présente un point de retournement à la date
? i i i
1 2
i, si ? 6 6 6 i = 1,2,...n-2
+ +
< >
> <
? 6 6 6
i i i
+ +
1 2
[1 ' int
si c est un pode retournement
Soit la variable aléatoire Xi = ?
t_0 sinon
La variable Xi suit la loi de Bernoulli de
paramètre p = 2/3
n-2
?x i
i=1
Le nombre total des points de retournement est p =
n 2
Nous avons : E (p) =
- ?= = 3 2 (n-2) ;
E(x )
i
i 1
? ( \ 1
2
n-2 40 n 2 - 144 n + 131
Donc Var (p) = 90
16 n - 29
E (p 2 ) = ? ? 1 I
E x
= 90
i
? ? ? ) I ?
i=1
Sous l'hypothèse que les ( 6 i )
forment une suite de variables aléatoires, indépendantes et
identiquement distribuées.
La statistique U =
suit la loi normale d'espérance nulle et de variance
égale à 1
p E(p)
-
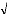
Var(p)
(U--* N (0,1) ; (n (nombre d'observations) > 30).
Le principe de ce test est d'accepter l'hypothèse que les
(6 i ) i (les résidus du
modèle) forment un bruit blanc si U < 1.96, au seuil a =
0.05.
è Test de la nullité de la moyenne des
résidus
Soit T le nombre de données disponibles
(après avoir enlevé les retards correspondant aux termes
AR et MA). Si le processus { e t , tE Z}
est i.i.d. (0, 2
oe ), nous devons avoir :
T
1
e t T e
= ? = 1 à
t
t ? 0
T ??
Par application du Théorème central limite, nous
montrons que :
TN?> L
T --*co
( , )
0 1
e t
à
o e t
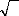
Dés lors, nous pouvons tester la nullité de la
moyenne des résidus en construisant l'intervalle de confiance sur e
t au seuil standard de 95%.
? ? _ . .
1,9 6 o à e o e
1,9 6 à
Pt
?? e E ? ,
t ?? ?
?T T
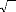
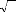
1 ? ? ?
= 0,95.
? ???j
Le test basé sur la statistique de Student pour tester
l'hypothèse
H0: « m=0 » contre
H1 : « m ~ 0 ».
e
t
La statistique utilisée est : t =
oe/ n-1
H0 Est acceptée si
t <t n ? 1 à 5% (=1,96) pour n
>30, dans le cas contraire, il convient d'ajouter

une constante au modèle. è Tests de
normalité
Le test de Jarque & Bera (1984) peut s'appliquer
pour tester la normalité des résidus.
Ce dernier est fondé sur la notion de Skewness
(l'asymétrie de la distribution, moment d'ordre 3) et de Kurtosis
(l'aplatissement qui se traduit en particulier par une épaisseur des
queues de distribution, moment d'ordre 4). Soit jUk le
moment empirique d'ordre k du
|
processus ? ?
p e e
= ? ?
1 à
T k
k t
T t = 1
|
.
|
o Test de Skewness
La Skewness est une mesure de l'asymétrie de la
distribution de la série autour de sa moyenne. Le coefficient de
Skewness (Sk ou encore J31 ) est
défini par :
L
( )1 2 1 2 3
S P ? 6 ?
? ? --* N J
( ) ?
k E P --*o 0,
1 3 2 T T
2 ? ?
La Skewness d'une distribution symétrique, telle que la
distribution normale est nulle. Une Skewness positive signifie que la
distribution a une queue allongée vers la droite et la Skewness
négative signifie que la distribution a une queue allongée vers
la gauche.
o Test de Kurtosis
La Kurtosis mesure le caractère pointu ou plat de la
distribution de la série. Le coefficient de Kurtosis (k u
ou encore J2) est défini par :
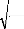
?
J .
?
P L ? 24
k N T
? - --*
4
J3 P --* o 3,
u 2 2 ?
T
2 ?
La Kurtosis de la distribution normale est 3. Si la Kurtosis est
supérieure à 3, la distribution est plutôt pointue
relativement à la normale ; si la Kurtosis est inférieure
à 3, la distribution est plutôt plate relativement à la
normale.

Nous construisons alors les statistiques centrées
réduites correspondantes à (Sk )
12 et ku que
l'on compare aux seuils d'une loi normale centrée
réduite
1 2
7 = 1
L k _ 3 L
( )
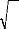
--* = --*
N et N
( ) ( )
u
0,1 7 0,1
2
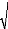
S k
6 T 24 T
--*o --*o
T T
Si la statistique centrée réduite de
(Sk ) 12 ( 71 ) est
inférieure au seuil 1,96 à 5%, nous acceptons
l'hypothèse de symétrie. Si la statistique
centrée réduite de ku
(72) est inférieure au seuil 1,96 à
5%, nous acceptons l'hypothèse de queue de distributions
non chargées (not weighted queues). La conjonction des deux conclusions
nous fait accepter l'hypothèse de normalité.
o Test de Jarque-Bera
La statistique de Jarque-Bera est une statistique de test pour
examiner si la série est normalement distribuée. La statistique
mesure la différence de la Skewness et de la Kurto sis de la
série avec ceux de la distribution normale. La statistique est
calculée comme suit :
|
JB S
=
|
T T
S +
6 24
k
|
?
( 3 ) ( 2)
- --*
2 z 2
k u
T--*o
|
Où Sk est la Skewness, k
u est la Kurtosis. Sous l'hypothèse nulle d'une
distribution normale, la statistique de Jarque-Bera suit asymptotiquement une
loi de 2
z à deux degrés de liberté ;
aussi,
si JB ( 2)
? ? 1 -- a nous rejetons l'hypothèse
H0 de normalité des résidus au seuil.
2
è Test d'indépendance de
Von-Neumann
Ce test peut être effectué lorsque les
résidus sont gaussiens.
Nous testons l'hypothèse nulle :
H0 : « Les résidus sont
indépendants et identiquement distribués » contre
l'hypothèse H1 : « Au moins deux observations
successives tendent à être corrélées ».
Les tests sont basés sur les deux estimateurs suivants de
la variance 2
?g des résidus :
2
n
D2= ? )
n g g
t t
? --
1 ?? 1
-- 1 t 1
n
2
; ( )
S g g
? ?
2 --
1 ?? t
n -- 1 t 1
?2
.
2 2
? (
Sous H0 : E ?
D = 1
--
D = 1 et Var ? 2
n
?
? 2S '2
J ? 2S 2 --
? n
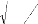
La statistique U = ( )
D S
2 2
2 ?
n
n 2 -- 1
-- 1
--
2
sous l'hypothèse nulle, suit une loi Normale N (0, 1).

La région critique est donnée par : { U
> U a }, U a est tel
que P{ U > Ua J = a.
è Test de Durbin-Watson
Si les résidus { g t , t Z}
obéissent à un bruit blanc, il ne doit pas exister
d'autocorrélation dans la série. Nous pouvons pour cela appliquer
le test suivant :
Test de Durbin - Watson : repose sur l'hypothèse de
normalité des résidus; test de l'autocorrélation d'ordre
1.
o Principe du test de Durbin -
Watson
Ce test permet de tester l'autocorrélation d'ordre 1 sous
l'hypothèse que les résidus sont Gaussiens. Donc il teste
l'hypothèse nulle
H0 : « p = 0 » contre
l'hypothèse alternative H1 : « p ~ 0
».Durbin et Watson ont proposé la
statistique suivante :
( )
g g
t t
-- -- 1
n
?
2
|
DW =
|
t
|
?
|
2
|
|
|
|
|
n
?
|
g
|
2 t
|
|
t
|
?
|
1
|
Le test de Durbin-Watson fait intervenir deux seuils critiques d
l,a et du ,a ( dl
,a < du ,a) fonctions
de n et du nombre de variables explicatives.
Ce test est utilisé pour tester trois hypothèses
:
1- H0 : « les
résidus sont non corrélés » contre H1:
« les résidus sont positivement corrélés »
Dans ce cas la règle de décision est : i)- Si DW
< dl ,a : nous rejetons H0.
ii)-Si DW > du ,a :nous acceptons
H0 .
iii)- Si dl ,a ~ DW ~ d u ,a
: nous ne pouvons rien dire.
2- H0 : « les
résidus sont non corrélés » contre H1:
« les résidus sont négativement
corrélés » la règle de décision
est :
i)- Si (4-DW) < dl ,a : nous rejetons
H0.
ii)- Si (4-DW) > d u ,a : nous acceptons
H0 .
iii)-Si dl ,a ~ (4-DW) ~ d u ,a
: nous ne pouvons rien dire.
3- H0 : « les
résidus sont non corrélés » contre H1:
« les résidus sont positivement ou négativement
corrélés »
Dans ce cas :
i) - Si DW < dl ,a2 ou (4-DW)
< dl ,a 2 : nous rejetons
H0.
ii) - Si DW > du ,a 2 ou (4-DW) > du
,a 2 : nous acceptons H0 .
iii)




- Si dl ,a 2 ? DW ~ du ,a 2
ou dl ,a 2 ? (4-DW)~ du ,a 2 : nous ne
pouvons rien dire.
è Test
d'homoscédasticité
L'hétéroscédasticité signifie que la
dispersion des résidus a tendance à augmenter ou à
diminuer en fonction des valeurs ajustées, plus
généralement, elle se manifeste quand la dispersion des
résidus varie en fonction des variables explicatives.
Non seulement L'hétéroscédasticité
influence les tests de significativité mais surtout, elle fausse les
intervalles de prévision.
Nous allons présenter, un test permettant de
détecter une hétéroscédasticité
éventuelle. Le test ARCH ou test du multiplicateur de Lagrange
a été introduit par Engle (1982). Supposons que les
résidus prévisionnels sont non corrélés et qu'ils
obéissent à un modèle ARCH (dans la plupart des
cas un modèle ARCH simple d'ordre p).
Nous construisons alors une régression entre les
résidus au carré et les résidus au carré
décalés jusqu'à l'ordre p.
L'hypothèse nulle testée est celle
d'homoscédasticité H0:"a1
= a2 =K K = a p = 0" contre L'hypothèse
alternative d'hétéroscédasticité conditionnelle
H ? i i = p tel que i
1 : " , 1 0"
K a.Si l'hypothèse H0 est
acceptée, la variance conditionnelle
de l'erreur est constante 0
a? 2 = a . En revanche, si l'hypothèse
nulle est rejetée, les résidus suivent un processus ARCH
(p) dont l'ordre p est à déterminer.
Le test est fondé soit sur un test de Fisher classique,
soit sur le test du Multiplicateur de Lagrange (LM). La mise en oeuvre
du test est simple et peut s'effectuer en trois étapes :
· Etape1 : nous estimons
l'équation de la moyenne. Nous récupérons les
résidus estimés ?àt et nous
calculons la série des 2
?àt .
· Etape 2 : Nous
régressons 2
?àt sur une constante et sur
ses p valeurs passées.
· Etape 3 : Nous calculons la
statistique du Multiplicateur de Lagrange LM = n*R2 où
n est le nombre d'observations servant au calcul de la
régression de l'étape 2 et R2 est le coefficient de
détermination de l'étape 2.
Sous l'hypothèse nulle d'homoscédasticité,
la statistique 2
TR suit une loi de khi - deux à
p
degré de liberté. La règle de
décision est :
- Si LM < ( )
z 2 p , l'hypothèse nulle est
acceptée : il n'existe pas d'effet ARCH.
- Si LM ~ ( )
z 2 p , nous rejetons
l'hypothèse nulle en faveur de l'hypothèse alternative
d'hétéroscédasticité conditionnelle.
Une autre approche consiste à calculer le
corrélogramme des résidus au carré du modèle
initial. Si les premiers termes de ce corrélogramme sont
significativement différents de zéro (0), alors nous pouvons
conclure à un modèle de type ARCH. Sinon si tous les
pics sont dans la bande de confiance, alors nous pouvons donc conclure que les
résidus sont homoscédastiques.
II.4.3 Choix du Meilleur Modèle
Après les étapes précédentes,
plusieurs formulations dans la vaste classe des modèles ARMA
pourraient être retenus ; il faut donc choisir le meilleur
modèle parmi ceux sélectionnés. Pour cela nous utilisons
:
s Les critères standards
Ils sont fondés sur le calcul de l'erreur de
prévision que l'on cherche à minimiser. Nous rappelons ici
l'expression des trois critères les plus fréquemment
utilisés.
-Erreur absolue moyenne (Mean Absolute Error)
-Racine de l'erreur quadratique moyenne (Root Mean Squared
Error)
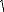
1
eà 2
t

N
?t
RMSE =
-Ecart absolu moyen en pourcentage (Mean Absolute Percent
Error)
|
1
MAPE = ?
100
N t
|
à
et
Xt
|
|
|
Où N est le nombre d'observation de la série X
t étudiée et
eàt désigne les résidus
estimés. Plus
la valeur de ces critères est faible, plus le
modèle estimé est proche des observations.
· Les Critères d'information
L'idée sous - jacente consiste à choisir un
modèle sur la base d'une mesure de l'écart entre la vraie loi
inconnue et le modèle estimé. Cette mesure peut être
fournie par la quantité d'information de Kullback. Les différents
critères ont alors pour objet d'estimer cette quantité
d'information. Il en existe plusieurs, Nous présentons ici les trois
critères les plus fréquemment employés.
a) Critère d'information d'Akaike (AIC)
(1969)
Le meilleur des modèles ARMA (p, q) est le
modèle qui minimise la statistique : AIC (p, q) = n Log
2
?àe + 2 (p+ q)
b) Critère d'information Bayésien
(BIC)
Ce critère présente l'avantage de pénaliser
les modèles où les paramètres sont en surnombre
comparativement à l'AIC. Il est donné par :
? ? ? ? ? 1
? 2
p q ? 1
BIC (p, q) = n Log 2
?àe - (n-p-q) Log
?J
?? 1 + (p+q) Log 2
? n ? ? ? ? ?
( ) à 1
?
p q e
? ? - J J
a e
c) Critère de Schwartz 1978
SC (p, q) = n Log 2
?àe + (p+ q) Log
n
d) Critère de Hannan-Quin
1979
[
HQ 69, q) = Log 6-:+ (p+ q) c Log Log
ni
Où c (c >2) est une constante.
n
Remarque : Le critère le plus
utilisé est le critère AIC. Cependant Hannan
(1980) a montré que seuls les estimations des ordres p et
q déduits des critères BIC et HQ sont
convergentes et conduisent à une sélection asymptotiquement
correcte du modèle.
Nous cherchons à minimiser ces différents
critères. Leurs applications nous permettent de retenir un modèle
parmi les divers processus ARMA validés. Ainsi s'achève
l'étape de validation. La dernière étape de la
méthodologie de Box & Jenkins est celle de la prévision.
· Principe de parcimonie
Lorsqu'on veut modéliser une série chronologique,
par un processus Stochastique et dans le cas où les critères
d'information AIC et BIC de deux ou plusieurs modèles
retenus seraient très proches ou contradictoires, nous faisons
intervenir ce principe qui cherche à minimiser le nombre de
paramètre requis; il est préférable de conserver un
modèle qui est ½moins bon½, mais qui contient moins de
paramètres.
II.5 Prévision
L'objectif de la modélisation de Box et Jenkins est la
prévision de futures valeurs de la série chronologique. A
l'horizon h la valeur de la prévision
Xà(t + h )notée
It (h ) est l'espérance conditionnelle de
X(t+ h) telle que :
Xàt (h )
= E(Xt+h / Xt ,
Xt--1 )
|
It (h )
|
est la prévision (la valeur estimée de X
t+h)
|
t :l'origine de la prévision.
h : l'horizon de la prévision
L'espérance conditionnelle de la prévision est
définie par : 1 -- X(t -- j)
X(t), X(t --1), ....,
X(1)}=X(t -- j), j>_0
2 Ef X(t+ j)
X(t),X(t--1),....,X(1)}=Yi(
j), j > 0
3 Ef e(t -- j)
X(t),X(t--1),....,X(1)}=e(t--
j), j 0 4 -- Ef e(t + j)
X(t), X(t --1), ...., X(1)}=0, j >
0
Nous considérons un processus ARIMA (p, d, q)
défini par :
?(L
)vdXt = (L
)et, t > 0
où 0(L) =E(AÉ,
0(L)= E0 avec 00 00 1, et
Vd (1-- L) i
p q
d
Nous pouvons écrire :
|
? ? ? ? ? ?
q q d d
d
? _ ? _ = ? _ ? ? ? _
1 1 1
? ? ?
O O
i ( ) ( )
i
i L L L L
i
? ? ? ? ?
j
i = 0 i j
= =
0 0
|
d j
_**
|
X t = 49 1 Xt _ 1 +
492X t _2 +
·
·
· + ÇO
p Xt _ p _ d
Où les çoi sont obtenus
à partir du développement de * * Pour un horizon h,
l'équation s'écrit:
p q q
+
X h E X t j X t X t ? X h ? e h i
u( ) ( ) u( ) $( )
t = + _ = ? _ ? _
( ) ( ), ( 1),... i t i t
i i
= =
1 1
0 pour i < h
où ( )
? _
å h-i
( )
t
pour i h
?
$ h i =
t r??
? L'erreur de prévision
Soit et+h l'erreur de la prévision à
l'instant t+h : ut+h
e t+h = X t+h - X
Nous notons que : E (e t+h) = 0, Var (e t+h) =
( )
1 + r 1 + r 2 +... +
r h _ 1 a e
2 2 2 2
Donc Xt + h ~ ( ( 2 ) 2
)
N Xt + h + 'T' + 'I' + + P h _
a
à , 1 1 ...
2 2
2 1
D'où les intervalles de confiance de la prévision
à (1-a )% donnée par :
à
X t h X t h Z a a
= #177;
+ + 1
( 1 ... );
+ q1 + q1 + + p
2 2 2
1 2 h _ 1
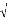
_
2
où ? _ 2 ?
Z est le quantile d'ordre ??
[\ 1 a de la loi normale centrée
réduite. Pour a = 5% Nous
1 a
_
2
avons :
X t h X t h 0
= #177;
à 1 . 9 6
+ +
( 2 )
1 1 ...
+ ? + ? + + ?
2 2
2 h _ 1

Les critères suivants sont utilisés pour juger la
validité de la méthode de prévision :
1
e e
= ? i
n i
1- L'erreur moyenne (Mean Error) ME
(e) =
n
= 1
|
n
2- La variance Var
(e) = ( )
n e e _
1 ?= i
i 1
|
2
|
|
n
1
3-
e 2
i
Le carré moyen des erreurs (Mean Square
Error) MSE (e ) = ?=
n 1
i
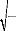
Très utilisé, car il pénalise un biais
éventuel dans la prévision.
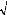
n
4- Root mean square error RMSE (e
) = MSE( ? ) = 2
1 ??
i
n i = 1
Conclusion
Ainsi s'achève la partie méthodologie de Box &
Jenkins; au chapitre suivant on passe à l'application
de cette méthode sur les séries étudiées.
Modélisation de la série SPY
Notation
La série SPY est l'actif qui correspond à la valeur
des actions de 500 compagnies les plus représentatives de
l'économie américaine. Il couvre la plupart des secteurs de
l'industrie et est échangé sur les marchés NASDAQ et NYSE
(New York Stock Exchange).
La valeur de l'actif SPY tient compte de la capitalisation
boursière des compagnies qu'il contient.
Identification
Les données de la série SPY s'étalent sur
une période de trois ans, les observations sont journalières ; du
03 janvier 2005 au 30 novembre 2007 soit 760 observations. L'unité de
mesure est le dollar américain.
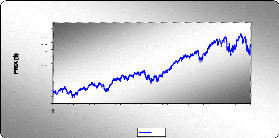
I- Analyse graphique
Graphe de la moyenne et de la variance de la série
brute SPY
D'après les deux graphes ci-dessous, on remarque que la
moyenne et la variance varient au cours du temps, donc on peut
appréhender la non stationnarité de cette série.
Pour vérifier ceci, on va appliquer des tests statistiques
juste après la présentation des corrélogrammes simple et
partiel de la série brute.
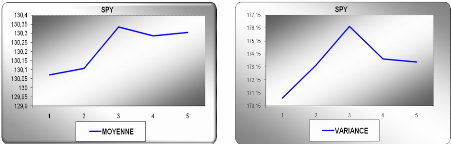
Diagramme séquentiel de la série brute
SPY
On voit clairement sur le graphe de la série brute que ce
processus est non stationnaire et cela provient tout naturellement de la
présence d'une tendance haussière.
165
160
155
150
145
140
135
130
125
120
115
110
105
56 111 166 221 276 331 386 441 496 551 606 661
716
TEMPS(JOURS)
GRAPHE DE LA SERIE SPY
SPY
Examen du corrélogramme de la série
SPY
On constate que la fonction d'autocorrélation simple
(colonne AC) décroit très lentement, cela est typique d'une
série non stationnaire. En revanche, la fonction
d'autocorrélation partielle (colonne PAC) a seulement son premier terme
significativement différent de 0 (l'intervalle de confiance est
stylisé par les pointillés).
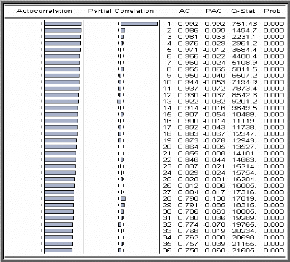
-Corrélogramme de la série SPY-
II -Analyse analytique
Application du test de Dickey- Fuller Augmenté
(DFA)
On procède à l'estimation par la méthode des
moindres carrés des trois modèles [1], [2] et [3] de
Dickey-Fuller sur la série SPY.
Remarque
On choisit le retard (d=1) qui minimise les critères
d'informations d'Akaike et Schwarz.
s Modèle [3]
|
d
A = + + â + A +
SPY q$ SPY ? c t q$ SPY e
t t 1 j t j t
?
j ? 1
Avec et est un processus stationnaire
|
.
|
On commence par tester la significativité de la tendance
en se référant aux tables de DickeyFuller. Le résultat du
test sur la série SPY est donné dans la table
suivante:
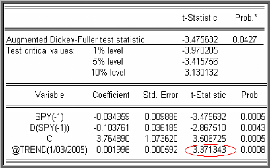
On compare la t-statistique du coefficient de la tendance
(@trend) avec la valeur donnée par la table de Dickey-Fuller. La
tendance est significativement différente de zéro puisque sa
statistique (3,37) est supérieure à la valeur critique (2,78) au
seuil 5%.
De plus la statistique de Student t?à = -3,4756
est inférieure à la valeur critique -3,4157
(donnée par la table de Dickey- Fuller)
pour le seuil 5%. D'où la série ne possède pas
une racine unitaire (on rejette l'hypothèse nulle «q$ =
0«).
Donc la série SPY est non stationnaire
de type TS, pour la stationnariser on a eu recours à un
ajustement linéaire, car le R2 associé est égal
à 0,918 (d'après les résultats obtenus par le logiciel
SPSS 10.0).
|
Dépendent
|
MTH
|
RSQ
|
D.F
|
F
|
SIGF
|
b0
|
b1
|
b2
|
b3
|
|
SPY
|
LIN
|
0,918
|
758
|
8458,49
|
0
|
108,406
|
0,0573
|
|
|
|
SPY
|
LOG
|
0,615
|
758
|
1208,9
|
0
|
71,087
|
10,4867
|
|
|
|
SPY
|
INV
|
0,041
|
758
|
32,26
|
0
|
130,773
|
-58,267
|
|
|
|
SPY
|
QUA
|
0,93
|
757
|
5017,82
|
0
|
111,648
|
0,0318
|
3,40E-05
|
|
|
SPY
|
CUB
|
0,938
|
756
|
3808,11
|
0
|
114,794
|
-0,0176
|
0,0002
|
-1,00E-07
|
|
SPY
|
COM
|
0,927
|
758
|
9584
|
0
|
109,689
|
1,0004
|
|
|
|
SPY
|
POW
|
0,638
|
758
|
1334,03
|
0
|
81,9846
|
0,0812
|
|
|
Remarque
On note la série ajustée par AJSPY,
elle est donnée par la formule suivante : AJSPY = SPY -
y(t).
Où y(t) est l'équation de la
tendance.
Estimation de la tendance:
L'estimation de l'équation de la tendance
y(t) est donnée par :
y(t)=b0 + bt 1
Les coefficients b0, b1
sont données par le tableau ci-dessus :
D`ou l`équation de la tendance est la suivante :
y(t)= 108, 406+ 0,0573t
Graphe de l'ajustement linéaire de la série
SPY
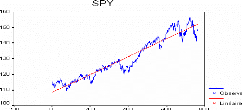
On remarque d'après ce graphe que la droite suit le
mouvement ascendant du graphe. Diagramme séquentiel de la
série ajustée AJSPY
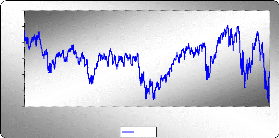
-12
12
-4
-8
4
8
0
1 51 101 151 201 251 301 351 401 451 501 551 601 651 701 751
AJSPY
D'après le graphe on constate que la série
AJSPY semble stationnaire. Pour confirmer cette supposition,
on va appliquer les tests statistiques appropriés.
Test de Dickey- Fuller Augmenté sur la
série AJSPY
On procède à l'estimation par la méthode des
moindres carrés des trois modèles [1], [2] et [3] de
Dickey-Fuller sur la série AJSPY.
Corrélogramme de la série AJSPY
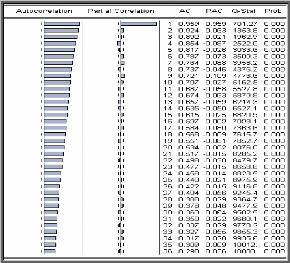
On voit que la fonction d'autocorrélation de la
série AJSPY décroit vers zéro et la première
autocorrélation partielle est clairement significative. Cette structure
est peut être celle d`une série stationnaire.
Pour confirmer cela, on fait appel aux tests de Dickey-Fuller
augmenté et de Fisher.
Test de Dickey- Fuller augmenté sur la
série AJSPY
On procède à l'estimation par la méthode des
moindres carrés des trois modèles [4], [5] et [6] de
Dickey-Fuller sur la série AJSPY.
Modèle [6]
|
d
A = + + â + ? A +
AJSPY AJSPY ? c t AJSP Y e
t t 1 j t j t
j ? 1
Avec et est un processus stationnaire.
|
.
|
On vérifie alors l'absence d'une tendance dans le
processus en testant la nullité du coefficient de la tendance
â. Le résultat du test pour la
série AJSPY est donné par la table
suivante :
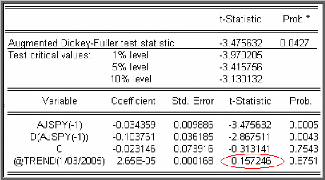
On remarque que la t- statistique de la tendance (= 0,157) est
inférieure aux valeurs critiques 3,48 ; 2,78 et 2,38 (données par
la table de Dickey- Fuller) pour les seuils 1%, 5% et 10%, on
le confirme par la probabilité 0,875 1 supérieure à
0,05.
Donc l'hypothèse nulle est bien entendu accepté, la
série AJSPY n'est pas affectée d'une tendance.
Modèle [5]
d
.
A = + C + A +
A JS P Y A JSP Y Çb A JS P Y ?
t t -1 j t j t
-
j ? 1
Après rejet du modèle [6], on procède au
test d'absence de la constante, dont le résultat est donné par la
table suivante :
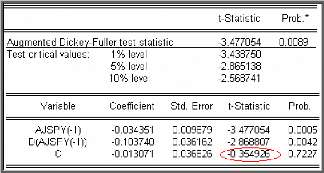
On remarque que la t-statistique de la constante (= -0,3549) est
inférieure aux valeurs critiques 3,72 ; 3,08 et 2,72 (données par
la table de Dickey- Fuller) pour les seuils 1%, 5% et 10%, on
le confirme par la probabilité 0,7227 supérieure à
0,05.
Donc, on rejette l'hypothèse de présence d'une
constante.
Modèle [4]
d
.
A = + A +
A JSP Y q$ A JSP Y ? q$ A JSP Y ?
t t j t j t
1 ?
j
?
1
On teste alors la présence d'une racine unitaire dans le
processus en vérifiant la nullité du paramètre q$
à l'aide d'une statistique de Student, où
q$à désigne l'estimateur des moindres
carrés ordinaires (MCO).
Le résultat du test pour la série AJSPY est
donné dans le tableau suivant :
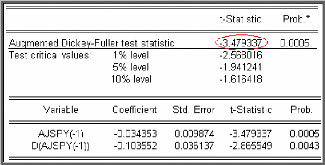
La statistique de Student (t?à = -3,4793 ) est
inférieure aux valeurs critiques -2,5680 ; -1,9412
et -1,6164 pour les seuils 1%, 5% et 10%, d'où la
série ne possède pas de racine unitaire (on rejette
l'hypothèse nulle «q$ = 0«).
Test de FISHER pour la série AJSPY
Pour détecter la saisonnalité de la série,
on a fait appel à l'analyse de la variance à deux facteurs sans
répétition.
TABLE DE l'ANOVA
|
SDV
|
SDC
|
DDL
|
Moyenne des carrés
|
Fc
|
Probabilité
|
Valeur critique pour F
|
|
Lignes
|
10130,7981
|
151
|
67,0913779
|
63,136
|
1,412E-292
|
1,22674639
|
|
Colonnes
|
2,81115108
|
4
|
0,70278777
|
0,661
|
0,61904387
|
2,38668545
|
|
Erreur
|
641,834829
|
604
|
1,06264045
|
|
|
|
|
Total
|
10775,444
|
759
|
|
|
|
|
Test d'influence du facteur colonne, la période
(jours : H0 = pas d'influence)
V
Calcul de la statistique de Fisher p
Fc ? que l'on compare
à la valeur théorique lue dans la
V R
table.
F v ;v à v 1 =p-1 et v 2 =(N-1)(p-1)
degrés de liberté.
á
1 2
F c = 0,66 1 ~ F v ;v =2,386 , donc on accepte
l'hypothèse nulle, la série n'est pas saisonnière.
á
1 2
Test d'influence du facteur ligne, la tendance
(H0 =pas d'influence du facteur
semaine)
' V S que l'on compare à la valeur
théorique 3 2
F v ;v à v 3 =N-1 et v 2
=(N-1)(p-1) degrés de
á
F =
c V R
liberté.
F c = 63,136 > F v ;v =1,226 ; donc on rejette
l'hypothèse nulle la série est peut être affectée
á
3 2
d'une tendance. Mais d'après le test de Dickey-Fuller la
tendance n'est pas significativement différent de zéro, car il
est plus précis que le test de Fisher pour la tendance.
Désignation
Vp : La variance de la période, VR:
la variance résiduelle, VS : la variance de la semaine, N:
nombre de semaines, p : le nombre d'observations
(périodicité) dans la semaine (jours p=5). En conclusion La
série AJSPY est donc stationnaire; c'est à dire
intégrée d'ordre 0. Estimation des paramètres du
modèle
Il convient à présent d'estimer le modèle
susceptible de représenter la série. En observant les
corrélogrammes simple et partiel de la série stationnaire AJSPY,
On remarque que la fonction d'autocorrélation simple (AC) possède
des valeurs importantes aux retards q= 1, 2, 3, 4, 5...; et la
fonction d'autocorrélation partielle (PAC) possède des valeurs
importantes aux retards p=1, 2,4.
Par conséquent on a plusieurs modèles candidats
parmi lesquels nous avons sélectionné deux modèles :
|
Modèles
|
AIC
|
BIC
|
|
ARMA (3, 3)
|
2,86
|
2,89
|
|
ARMA (4, 2)
|
2,86
|
2,89
|
On a choisi le modèle ARMA (3, 3) d'après le
critère de parcimonie, car les deux modèles ont les mêmes
valeurs de AIC et BIC.
Estimation du processus ARMA (3,3)
L'estimation des processus ARMA repose sur la méthode du
maximum de vraisemblance. On
suppose que les résidus suivent une loi normale de moyenne
nulle et de variance 2
o? .
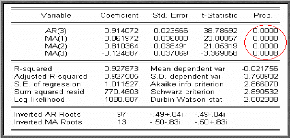
L'étape d'estimation achevée, l'étape
suivante permet de valider ou non le modèle estimé.
Validation du processus ARMA (3,3)
Test sur les paramètres
On remarque que tous les paramètres du modèle sont
significativement différents de zéro. En effet les statistiques
de Student associées sont en valeur absolue supérieurs à
1,96, ce qui est confirmé par les probabilités de
nullité des coefficients qui sont toutes inférieures à
0, 05(voir tableau estimation du processus
précédent).
Graphique des inverses des racines
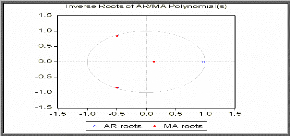
D'après la représentation graphique des inverses
des racines des polynômes de retards moyenne mobile et
autorégressif on s'aperçoit qu'ils sont tous supérieurs
à 1 en module (leurs inverses sont en module, inférieurs à
1).
Graphique des séries résiduelles
réelles et estimées
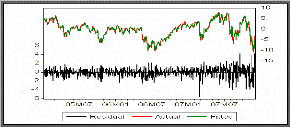
A partir de la représentation graphique des séries
résiduelles réelles et estimées nous constatons que le
modèle estimé ajuste parfaitement la série AJSPY.
Il convient maintenant d'analyser les résidus à
partir de leur fonction d'autocorrélation et d'appliquer une
série de tests.
Tests sur les résidus
$ $ ( )
Ces tests ont pour objet de vérifier la blancheur des
résidus estimés ( u L X
ê t =
t ) en
? $ ( )
L
appliquant des tests d'absence d'autocorrélation et des
tests d'homoscédasticité. Tests d'absence
d'autocorrélation
Il existe un grand nombre de tests d'absence
d'autocorrélation, les plus connus étant ceux de Box et Pierce
(1970) et Ljung et Box (1978), test des points de retournements dont on
rappelle brièvement le principe ci-dessous.
s Test de Box - Ljung
On a à tester l'hypothèse nulle
:
H0 : « Les autocorrélations
jusqu'au pas K, (K=N/5) ne sont pas significatives » C'est-à-dire
H0 : « p1 = p2
=... ? pK = 0 » Contre H1 : «
?p j : j = 1,K ,99 tel que pj ~ 0
».
2
.
K
Ce test est basé sur la statistique de Box-Ljung au pas k
: E ? ?
Q n n
= +
( 1) Y k
n k
k 1
Si 2
Q ? ? 0,95 ( K - p - q
- P - Q ) , nous acceptons l'hypothèse H
0 .
Les valeurs de la statistique de Box-Ljung ont de fortes
probabilités. Ce qui entraîne à dire que les résidus
forment un bruit blanc.
Corrélogramme simple et partiel des
résidus
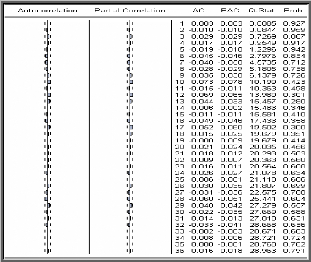
La probabilité de la statistique de Box-Ljung est
supérieure à 0,05 pour tous les retards et la valeur de la
statistique de Box-Ljung quand k = 99, p = 3, q = 3, P = 0 et Q = 0
égale à 62,153 est inférieure à 2
?0., 95 (93) = 116,51 ; On conclue alors que les
erreurs ne sont pas corrélées.
Conclusion
Les résultats du test de Box - Ljung sont identiques
à ce qu'on a remarqué de visu sur les corrélogrammes
simple et partiel.
s Test des points de retournements
Il s'agit de tester l'hypothèse nulle :
H0 : « Les ei sont
aléatoires » contre
H1 : « Il existe une corrélation
entre les ei i = 1,..., n ».
Après les calculs à l'aide du Visual Basic on a
obtenu les résultats suivants :
n - 2
|
Le nombre des points de retournements égal à P =
?
|
Xi = 490
|
i = 1
On a : n = 754 donc 2
E P n et Var P -
16 29 n
( ) ( 2) 504,66 ( ) 134.61
= - = = =
3 90
VAR ( P ) = 11,602 , ( ) 1,26
P E P
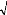
-
S = 1.26< S (tabulée) = 1,96
S = = - . Donc :
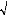
Var P
( )
Alors, on accepte l'hypothèse H0 :
« les résidus sont aléatoires ».
s Test de nullité de la moyenne des
résidus
Pour tester l'hypothèse H0: « m=0
» contre H1 : « m ~ 0 » on utilise le test
de Student
? t
.
o?/ n-1
basé sur la statistique : t =
Si t < tn-1 à
5% (=1,96) on accepte l'hypothèse de nullité de la moyenne des
résidus
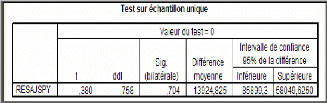
|
D'après le Tableau ci-dessus on a :
|
t = 0,3 80 qui est inférieure à 1,96; Donc on
accepte
|
l'hypothèse H0: « la moyenne des
résidus est nulle ».
s Tests de normalité sur les résidus du
modèle optimal
Les tests sont effectués à partir des valeurs
empiriques des coefficients de Skewness, Kurtosis et la statistique de
Jarque-Bera données par le logiciel EVIEWS 5.0. En utilisant le logiciel
on a l'histogramme suivant :
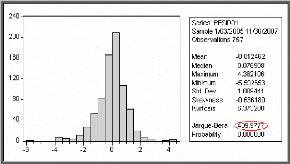
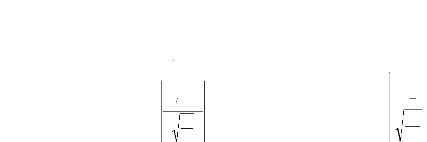
s Test de Skewness (asymétrie) et de Kurtosis
(aplatissement)
7 7
1 2
~ ?
0 0
ou
:
H0
:
2 -
0
71
6
= fi1 1
Coefficient de Skewness :
3
fi2
=
7
2
24
N
?
??
On teste les hypothèses suivantes :
?1
77 1 2
= =
0 0
et
H1
Coefficient de Kurtosis :
N
P
Où : 3 2
fi =
1 2 3 : est le coefficient de Skewness (l'indicateur
d'asymétrie des résidus).
1 P2
P
fi = : est le coefficient de Kurtosis (le degré
d'aplatissement de la loi des résidus).
4
P 2
2 2
Sous l'hypothèse H0 et si le nombre
d'observations est assez grand (N >30), on a :
P ?
????
N N
L 0,
--oo ?
?
6 ? ???????? ( )
1 .
N ? ?
fi
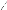
1 23
1 3 2
=
P 2


12 -
fi1
P 4
|
fi =
2 2
P 2
|
?
????
N N
L
?? ?
?
|
24 ?
0, N ? ?
|
|
( )
2
|
|
Après calculs on a obtenu :

6
N
71
-
24
Test de Skewness:
Test de Kurtosis:
0 = 6,93 > 1, 96.
3 = 19,03 > 1,96.
N
Alors, les résidus ne sont pas gaussiens. Ce qui est
confirmé par le test de Jarque et Bera s Test de Jarque et
Bera
On définit la statistique S par : S = ( )2
N N
fi ?
1 2 3
fi -
6 24
Sous (1) et (2) : S( 2)
3 Z 1 - a
2
On teste H0 : « accepter la
normalité des résidus au seuil a =0,05 » contre
H1 : « Il n'y a pas de normalité des
résidus ».
Si S ( 2)
> Z 1 _ a on rejette l'hypothèse
H0 sinon on l'accepte.
2
D'après le tableau la statistique de Jarque et Bera
notée (S) est égale à 409,9777 ; elle est
supérieure à (2)
Z = 5,99.
2
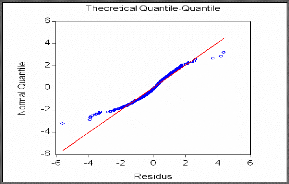
s Test QQ-Plot (méthode graphique)
Le nuage de point (en bleu) est formé par (quantiles de
N(0,1), quantiles empiriques réduits des résidus), sous H0 le
nuage est rectiligne sur la droite rouge y=x )
On remarque que le nuage de point n'est pas rectiligne sur la
droite, donc l'hypothèse nulle est rejetée c'est-à-dire
les résidus ne suivent pas une loi normale.
On affirme donc que les résidus forment un bruit blanc non
gaussien.
Remarque
On ne peut pas appliquer le test de Durbin-Watson et le test
d'indépendance de Von Neumann puisque les résidus ne sont pas
gaussiens.
Test d'homoscédasticité
s Test d'effet ARCH
Une première observation du graphe des résidus
ci-dessous montre que la moyenne de cette série est constante alors que
sa variance change au cours du temps. De plus le processus étant non
gaussien, on suspecte la présence d'un effet ARCH.
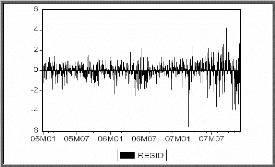
Corrélogrammes simple et partiel des
résidus au carré
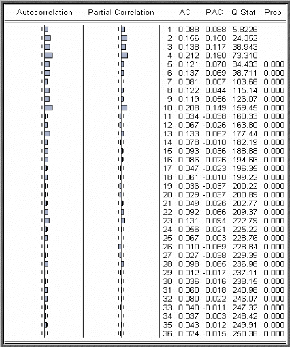
A partir du Corrélogramme on remarque plusieurs termes
significativement différents de zéro cela veut dire qu'il y a
certainement un effet ARCH. Pour cela on est passé au test
d'homoscédasticité dont le résultat est sur le tableau
ci-dessous :
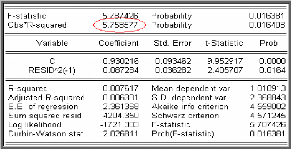
On a la statistique du multiplicateur de Lagrange
(n*R2) = 5,7585 qui est supérieure à z2 (1) =
3,84, on rejette l'hypothèse nulle d'homoscédasticité en
faveur de l'hypothèse alternative
d'hétéroscedasticité conditionnelle.
Identification du modèle de type ARCH
On a eu plusieurs modèles ARCH avec des ordres p assez
grands. Par conséquent on est passé au modèle GARCH
(1,1).
Les résultats obtenus dans la table ci-dessous montrent
que les paramètres de l'équation de la variance conditionnelle
sont significativement différents de zéro.
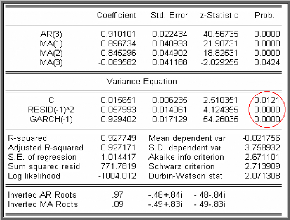
Le modèle retenu avec erreur GARCH (1, 1) s'écrit
sous la forme suivante :
(1 0,91 ) (1 0,89 0,85 0,08 )
- = + + -
B AJSPY B B B
3 2 3 & t
?
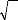
? ? =
& 17h 17 :
IID ( )
0, 1
t t t t
? ?L = + +
h h
0,0156 0,057 0.929
& - -
2
t t t
1 1
Prévision
Pour faire des prévisions, on remplace t par t+h dans
l'expression ci-dessus du modèle générateur de la
série.
On a par la suite
|
Observation
|
Prévision
|
Valeur réelle
|
Borne Inf
|
Borne Sup
|
|
761
|
148,71
|
147
|
144,84
|
152,70
|
|
762
|
148,96
|
145,59
|
143,54
|
154,56
|
|
763
|
148,99
|
148,02
|
142,55
|
155,41
|
|
764
|
149,18
|
150,14
|
142,09
|
156,40
|
|
765
|
149,41
|
150,11
|
141,54
|
157,47
|
Graphe de la série réelle et la
série prévue
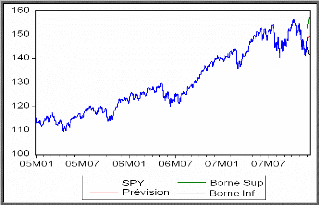
Modélisation de la série IEV
Notation
La série IEV est l'actif qui correspond à la valeur
des actions de 350 sociétés économiques qui sont
représentatives de l'économie européenne. Cet actif mesure
la performance des actions de compagnies en Autriche, Belgique, Danemark,
Finlande, France, Allemagne, Grèce, Italie, Pays Bas, Norvège,
Portugal, Espagne, Suède, Suisse et Grande-Bretagne.
Identification Les données de la
série IEV s'étalent sur une période de trois ans, les
observations sont journalières ; du 03 janvier 2005 au 30 novembre 2007
soit 760 observations. L'unité de mesure est le dollar
américain.
I- Analyse graphique
Graphe de la moyenne et la variance de la série
brute IEV
D'après les deux graphes ci-dessous, on remarque que la
moyenne et la variance varient au cours du temps, donc on peut
appréhender la non stationnarité de cette série.
Pour vérifier ceci, on va appliquer des tests statistiques
juste après la présentation des corrélogrammes simple et
partiel de la série brute.
93,74
93,62
93,38
93,26
93,14
93,02
93,5
92,9
1 2 3 4 5
IEV
MOYENNE
271
270
269
268
267
266
265
264
263
262
261
260
1 2 3 4 5
IEV
VARIANCE
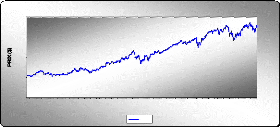
Diagramme séquentiel de la série brute
IEV
On voit clairement sur le graphique de la série brute que
ce processus est non stationnaire et cela provient tout naturellement la
présence d'une tendance haussière.
130
120
110
100
90
80
70
60
50
1 71 141 211 281 351 421 491 561 631 701
TEMPS (JOURS)
IEV
GRAPHE DE LA SERIE BRUTE IEV
Examen du corrélogramme de la série
IEV
On constate que la fonction d'autocorrélation simple
(colonne AC) décroît très lentement, cela est typique d'une
série non stationnaire. En revanche, la fonction
d'autocorrélation partielle (colonne PAC) a seulement son premier terme
significativement différent de 0 (l'intervalle de confiance est
stylisé par les pointillés).
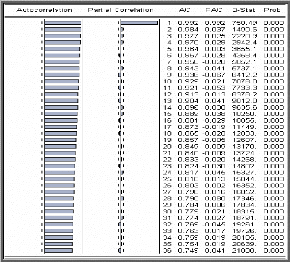
-Corrélogramme de la série IEV-
| 


