1.19. MONTE CARLO :
Les méthodes Monté Carlo consistent en des
simulations expérimentales ou
informatiques de problèmes mathématiques ou
physiques, basées sur le tirage de
nombres aléatoires. Généralement on
utilise en fait des séries de nombres pseudo-
aléatoires générées par des
algorithmes spécialisés. Les propriétés de ces
séries sont
très proches de celles d'une véritable suite
aléatoire. La méthode Monté Carlo est
également utilisée dans le domaine pharmaceutique
: on génère un vitro de très
nombreuses molécules aléatoires, puis on les
passe au crible en testant leur effet sur tel
ou tel cible. On repère ainsi des molécules
intéressantes qui après une étude et une
modification pourront donner naissance à de nouveaux
médicaments. L'orientation
actuelle est même de réaliser la même chose
en silico, c'est-à-dire de modéliser et de
tester ces molécules dans un ordinateur. Le grand
avantage de cette méthode est sa
simplicité. Elle permet entre autres de visualiser
l'effet de différents paramètres et de
donner ainsi des orientations, d'étudier des structures
intéressantes qui auraient été a
priori écartées et de trouver facilement des
structures que l'on n'aurait pas aussi bien
optimisées « à la main ». [69].
Les méthodes de types Monté Carlo recherchent
l'optimum d'une fonction en
générant une suite aléatoire de nombres en
fonction d'une loi uniforme.
Algorithme :
1ere Etape :
On génère un point initial x dans l'espace
d'état, considéré comme solution courante.
2emeEtape :
On génère aléatoirement un point x'.
3emeEtape :
Si x' est meilleur que x alors x' devient la solution
courante.
3emeEtape :
Si le critère d'arrêt est satisfait alors fin sinon
retour en à la deuxième étape [68]
1.2 0. OPTIMISATION PAR ESSAIM DE PARTICULES :
Observez un champ entrain d'être labouré en
automne, lorsque le soc de la charrue
pénètre le sol pour la première fois le
champ est vide de tout goéland et quelques
minutes après une nuée accompagne le tracteur. Au
début du labour un oiseau découvre
la source de nourriture et très rapidement un autre
arrive et ainsi de suite. Que s'est il
passé ? L'information concernant un festin potentiel
s'est largement diffusée au sein du
groupe de goéland. Les goélands volaient à
la recherche de nourriture de façon plus ou
moins ordonnée et le rassemblement s'est effectué
par un échange (volontaire ou non)
social d'informations entre individus de la même
espèce. L'un d'entre_eux à trouvé une
solution et les autres se sont adaptés en copiant sa
solution, ceci offre un caractère
adaptatif à la méthode. Au départ J.
Kennedy et R. Eberhart (Kennedy and Eberhart,
1995) cherchaient à simuler la capacité des
oiseaux à voler de façon synchrone et leur
aptitude à changer brusquement de direction tout en
restant en une formation optimale.
Le modèle qu'ils ont proposé à ensuite
été étendu en un algorithme simple et efficace.
Les particules sont les individus et elles se déplacent
dans l'hyperespace de recherche.
Le processus de recherche est basé sur deux règles
:
1) Chaque particule est dotée d'une mémoire qui
lui permet de mémoriser le
meilleur point par lequel elle est déjà
passée et elle a tendance à retourner vers ce point.
2) Chaque particule est informée du meilleur point connu
au sein de son voisinage
et elle va tendre à aller vers ce point.
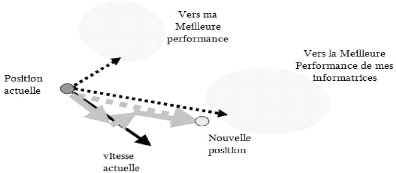
Figure 14: Schéma de principe du déplacement
d'une particule. Pour réaliser son
prochain
mouvement, chaque particule combine trois tendances : suivre sa
vitesse propre, revenir
vers
sa meilleure performance, aller vers la meilleure performance
de ses informatrices.
1.2 1. METHODES DE RESOLUTION
Actuellement, il existe une large gamme de méthodes
d'optimisation et une
multitude de variantes pour les mêmes algorithmes. Ces
méthodes sont utilisées en
respectant des contraintes de type égalité et
inégalité et en se basant, généralement, sur
le schéma suivant (Figure 13) :
Etat initiale de Répartition de
Figure 16Structure dun OP
Solution Optimale
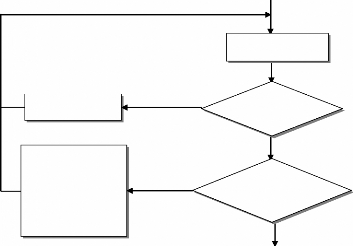
Optimisation
Changer:
§ Object
ifs
§ Contr
ôles
Non
Non
Convergenc
e
Résultats
Acceptable
Optimisation
Oui
Oui
Figure 15:Structure d'un OPF
| 


