3.1.15. Application
La fonction objective considérée dans notre cas
est la fonction des pertes actives
totales transmises. Le problème d'optimisation
répond aux équations suivantes :
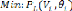
Sous les contraintes :
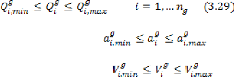
Avec :
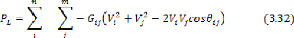
Où :
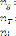
Nombre de générateurs.
Nombre de transformateurs.
Nombre de noeuds.
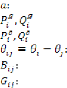
Rapport de transformation des transformateurs.
: Puissances active et réactive
générées dans le noeud i.
: Puissances active et réactive de charge dans le noeud
i.
Angles des tensions aux noeuds i et j.
Sus ceptance entre les noeuds i et j.
Conductance entre les noeuds i et j.
Dans notre étude, nous sommes intéressés
à l'étude de trois variantes. Les deux

premières concernent un seul type de variables de
contrôle. Il s'agit de
et de , alors que la troisième consiste à tenir
compte des deux types de variables
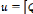
de contrôle, c'est à dire, . Dans les trois cas les
variables d'état sont :

3.1.16. Variante 1 : ( )
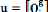

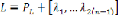
En appliquant l'expression (6.6), en forme matricielle, on
obtient :
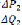
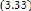
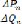
Les conditions d'optimisations, selon les expressions (3.2 0),
(3.2 1), (3.2 2) sont :
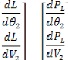
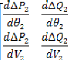
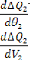
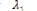



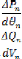
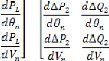
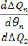
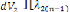

Et :
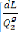
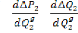
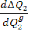
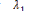
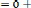
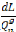
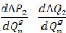
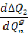
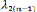
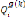
Et :
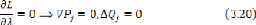

De l'équation (3.3 6), on obtient les valeurs du vecteur
des Ces derniers sont
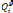
remplacés dans l'équation (3.37), pour
déterminer le vecteur Gradient des :
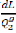
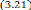
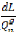
Commençons par le vecteur , on obtient les
différentes nouvelles valeurs des
puissances réactives aux noeuds de
génération par :
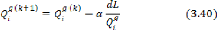
| 


