Utilisation des méthodes d'optimisations métaheuristiques pour la résolution du problème de répartition optimale de la puissance dans les réseaux électriques

II.5 Formulation mathématique du problème du Dispatching Economique :

Le problème du dispatching économique consiste à minimiser le coût total du combustible (C), sujet à une seule contrainte d'égalité qui est la somme de toute les puissances générées est égale à la puissance totale demandée (Pd).

Mathématiquement on peut écrire

ng ng

Minimiser ? ( ) ? (

C = C P = + . + . (II-01)

P ² )

i gi i i gi

P i gi

i = 1 i = 1

Dans la pratique, chaque puissance générée ( P_gi ) est limitée par une limite inférieure ( Pgi min ) et une autre supérieure( Pgi max ) , ce qui donne la contrainte d'inégalité suivante

P gi min = P gi = P gi max i=1,2,...,ng (II-03)

II.5.1 La méthode Lambda :

Le problème d'optimisation devient comme suit :

ng

Minimise : ?

F = F _i P gi

( )

i=1

ng A condition que : 0 H = ?= - = P gi P d i 1

(II-04)

Le système de équation (II-04) est un problème d'optimisation non linéaire avec contraintes, qui doit résoudre par le développement d'une fonction s'appelle la fonction de Lagrange.

Pour obtenir l'extremum d'une fonction objective, on doit ajouter la fonction de contrainte à la fonction objective, par la multiplicateur de Lagrange, qui préalablement indéterminé.

La fonction augmentée de Lagrange du problème est donnée par :

L = F + . H

La condition nécessaire pour avoir l'optimum est quand les dérivée premières de la fonction de Lagrange par rapport aux P_gi et sont égales à zéro.

Dans ce cas on a ng+1 variables, les inconnues sont les puissances générées et le multiplicateur de Lagrange.

La dérivée de la fonction de Lagrange par rapport à ne donne que la contrainte d'égalité. D'une autre façon, les puissances générées P_gi optimales sont obtenues quand les dérivées de la fonction

du coût par rapport aux puissances générées soient égales à zéro, en respectant que leurs sommes soit égale à la puissance demandée totale.

On obtient l'équation suivante des dérivées :

?L ?Fi	0
?Pgi P ? gi

F

Donc : i

i

? = = IC

?Pgi

IC_i: S'appelle l'incrément du coût

Donc, la condition d'existence d'un optimum pour la fonction de coût des centrales électrique thermique, et que l'incrément du coût IC_i , soit égale pour chaque générateur, une même valeur,

préalablement indéterminée qui est .

Et bien, pour cette condition on doit ajoute une contrainte d'égalité, la somme des puissances générées égale la puissance demandée total.

La contrainte d'inégalité est que les puissances générées ne dépassent pas ses limites. On résume le problème comme suit :

? F i
? P gi

ng équations.

P g min = P gi = P g max ng inégalités. (II-05)

ng

?= Pgi = i 1

P d

Une équation.

Pour le problème des violations des contraintes d'inégalités, on peut augmenter le système des équations (II-05) par l'ensemble d'équations :

? F i
? P gi

? F i
? P gi

? F i
? P gi

Pour P g min = P gi = Pgmax

= Pour P_gi = Pg max

= Pour P_gi = Pg min

Si certains générateurs dépassent sa limite, on prend cette limite, et on continue le processus de calcul pour les autres.

La valeur de lambda initiale doit être comprise entre _min et _max correspondants respectivement

aux Pg min et Pg max

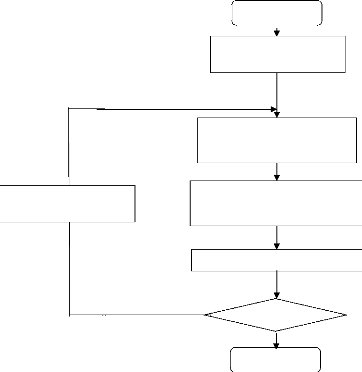
- L'algorithme de la méthode lambda :

Donner à une valeur
initiale

Non

Oui

Imprimer

Calcule nouvelle valeur
de lambda

Si P gi = P g min pose P gi = P g min
Si P gi = P g max pose P gi = P g max

Calcule les puissances
générées P_gi pour i=1,2...ng

Critère d'arrêt atteint

Calcule å =Ó pgi-Pd

Début

Figure II- 5 : Organigramme de la méthode lambda

II.5.2 Solution du problème du Dispatching Economique sans pertes

Pour résoudre le problème du dispatching économique, on fait appel à la fonction de Lagrange, formulée comme suit

? ng ( ) ?

? - ?

ng

2

+

L = . + . + ? = ?

P (II-06)

i i gi

P i gi

P P d gi

i = 1 ? i 1 ?

Est le multiplicateur de Lagrange. Les conditions nécessaires pour un minimum sont données par

? L = . + 2 . - = 0 (II-07)

i i gi

? P gi

P

ng

L = -

P d P gi = 0 i 1,2,..., ng

=

(II-08)

? ?=

? i 1

P gi min = P gi = P g i max

Donc, pour un fonctionnement optimal des générateurs, il faut que le l'accroissement du coût de tout les générateurs soit le même, c-a-d égal à( ) .

Le système d'équations (II-08) comporte (ng + 1) équations avec (ng + 1) inconnus, qui peuvent

êtres résolues par la substitution des valeurs de ( P_gi ) des premières équations dans l'avant dernière

-

i

i

P gi

2

=

ng

-

?=

i 1

i

P d

=

2 i

i 1,2,..., ng

=

(II-09)

La valeur optimale de ( ) est alors calculée comme suit

ng

*

P_d +

i

i

? 2 1

=	=				(II-10)
		ng ?	1
		1		i

La valeur optimale * est remplacée dans les premières équations de (II-09) pour obtenir la puissance optimale à générer par chaque générateur

Pgi

2

? ? 1 ? ? i ? ?

P d

ng

?

+ ?

i ?

2

1 ?

i - (II-11)

ng

?

1

i ?

1 ?

i ?

II.5.3 Solution du problème Dispatching Economique avec considération des pertes

Dans les systèmes réels, le transport de l'énergie électrique vers les jeux de barre de charge est souvent accompagné par des pertes de transmission. Le problème du dispatching économique devient un peu compliqué par rapport au cas précédent où les pertes ont été négligées.

Dans ce cas, la contrainte d'égalité représentée par l'équation d'équilibre de puissance donnée dans (2.3) doit inclure ces pertes. Si on désigne par PL les pertes totales de puissances actives, la contrainte d'égalité devient

ng

? P gi = P _d + P (II-12)

L

i=1

Le lagrangien est alors formulé par

? ? (II-13)

?

ng ng

?

L = ? ( + . P + . P ² ) + ? P P

+ - ? P

i= 1 ? i= 1

i i gi i gi d L gi

Les conditions nécessaires pour un minimum sont données par

0

? L ? ? P ?

L

= +

. 2 . P - -

?? 1 ??

i i gi

? P ? P

gi ? gi ?

ng ? L = + - P d P L ?= P gi ? i 1

0

i 1,2,..., ng =

(II-14)

P gi min = P gi = P g i max

Les pertes de puissances actives dans le système électrique, P_L sont fonctions des impédances du réseau et des courants qui transitent dans les différentes branches du système électrique [4].

On peut donc considérer que les courants sont fonction des variables indépendantes, P_gi et p_d .

La première équation de l'expression II-14, nous donne une relation directe entre la puissance générée ( P_gi ) et le multiplicateur de Lagrange( ) , donnée par

dC

i

i

dP

gi

(II-15)

dC

=

=

.

?P_L

1

L i

gi

dP

? Pgi

1

Le terme =

L =

1

i ? P L

est appelé : facteur de pénalité du générateur i.

? P gi

Remarques

Il existe trois approches générales pour résoudre le problème du dispatching économique avec pertes de puissance

1. La première approche consiste à considérer les pertes de puissances actives constantes, dans la contrainte d'égalité donnée par l'équation (II-12).

2. La deuxième approche consiste à développer une expression mathématique des pertes de puissances actives, en fonction des puissances actives des générateurs. Celle-ci est connue par la méthode de « formule des pertes », ou méthode des « coefficients B »

3. La troisième approche consiste à introduire les équations de l'écoulement de puissance comme contraintes essentielles dans la formulation du problème d'optimisation. Cette approche est connue par l'Ecoulement de puissance optimal [12] [02].