Estimation de l'erreur de trocature de l'espace d'états du système d'attente m/m1: méthode stabilité forte

3.5 Conclusion

Dans ce chapitre, nous avons introduit une synthèse bibliographique sur le concept de la chaàýne de Markov tronquée. Ensuite, nous avons donnédeux exemples différents sur l'application de la technique de troncature, que nous avons illustrépar quelque exemples. Dans le prochain chapitre, nous nous intéressons a` l'application de ces techniques de troncature sur le cas de la file d'attente M/M/1, o`u nous estimerons également l'erreur due a` ces troncatures a` l'aide de la méthode de stabilitéforte.

4

Calcul de la borne de stabilitéforte pour le

cas de troncature de la capacitéd'attente de

la file M/M/1

Ces dernière ann'ees, la m'ethode de stabilit'e forte a 'et'e appliqu'ee pour divers problèmes et sur plusieurs modèles stochastiques qui peuvent être r'egis par des chaàýnes de Markov homogènes.

Dans ce chapitre, on s'int'eressera au cas d'application de la m'ethode de stabilit'e tout en consid'erant le problème de la troncature de l'espace des 'etats de la chaàýne de Markov d'ecrivant la file M/M/1. Notre objectif est de faire une 'etude comparative entre deux techniques de troncature (augmentation de la première colonne et augmentation uniforme) pour le cas de calcul de la borne de stabilit'e forte.

4.1 Préliminaires et notations

L'outil principal utilis'e dans notre travail est la norme v not'ee .k_õ, o`u v est un vecteur dont les 'el'ements v(s) > 1 pour tout s ? S (S est l'espace des 'etats de la chaàýne de Markov) et pour tout w ? R^S on a par d'efinition:

kwkõ = sup i?S

w(i) v(i) .

Soit ,t une mesure de probabilit'e dans S, alors la norme v de ,t est d'efinie comme suit:

Calcul de la borne de stabilit'e forte pour le cas de troncature de la capacit'e d'attente de la file M/M/1 Page 48

X kukõ = i?S

v(i)ui.

La norme v est 'elargie aux noyaux de transition dans S. Dans ce cas, soit A ? R^S×S alors :

MAIõ = sup i,kwk=1	PS j=1	|A(i,j)w(j)|
		v(i) .

Supposons que ^-7 et 7 possedent une norme v finie, alors

|e7f - 7f| = ke7 - 7kõkfkõ inf i?S

v(i).

4.1.1 Borne de la stabilit'e forte

Le critere de stabilit'e forte est donn'ee dans le th'eoreme suivant.

Th'eor`eme 4.1 (Aissani et Kartashov 1983 [3]) :

Soit X une chaine de Markov de noyau de transition P et de mesure invariante 7, cette chaine est dite v - fortement stable par rapport a` la norme 11 · k_v, si elle existe une mesure invariante ó et une fonction mesurable non n'egative h sur N, satisfaisant les conditions suivantes :

a) 7h > 0, ó1I = 1, óh > 0, et

b) T = P - h ? ó est non n'egatif,

c) ||T||_v < 1,

d) 1P1_v < 8.

O`u ? repr'esente le produit de la convolution entre la mesure ó et la fonction h et 1I est un vecteur dont tout les 'el'ements sont 'egaux a` 1.

Ce r'esultat nous permet de d'elimiter le domaine des valeurs de perturbation de la norme v (]1, â0]) pour lequel la chaine de Markov en question est v-fortement stable.

La borne de la m'ethode de stabilit'e est donn'ee dans le th'eoreme suivant.

Th'eor`eme 4.2 ([31]) :

Soit P un noyau de transition v - fortement stable si :

|| Pe -P|| 1 - 11T11_õ

õ < ||I

- Ð||õ, (4.1)

alors la borne de la stabilit'e forte peut s''ecrire sous la forme suivante :

||e7 -- Ð||_v || 7||_õ = Dr||õ ||I

P^e- P||_õ

(4.2)

P- P||_õ^.

1 - kT k_õ - ||I - Ð||_õ ||

En g'en'eral, la constante ||I - Ð||_õ est estim'ee par 1 + 171_õ.

4.2 Troncature de la capacitéd'attente de la file M/M/1

Dans cette section, nous introduisons les résultats théoriques obtenus lors de l'étude de la stabilitéforte de la chaàýne de Markov dans un système de files d'attente M/M/1 après la troncature de la capacitéde la file d'attente par les deux techniques : augmentation de la première colonne et augmentation uniforme.

4.2.1 Description du modèle et position du problème

Considérons un système de files d'attente M/M/1, le flux des arrivées est poissonnien de paramètre A, et le temps de service est une variable aléatoire suivant une loi exponentielle de paramètre u.

Notons par Q = A/u la charge (ou l'intensitédu trafic) de ce système

Le noyau de transition Pe = (^fPij)i,j>0 associéau modèle d'attente M/M/1 est défini comme suit :

^ePij =

? ??? ???

a, si i = j = 0; a, si j = i + 1; a, si j = i - 1,i > 0; 0, ailleurs,

o`u a = A/(A + u) et a = (1 - a) = u/(A + u).

On a, Pe = (^fPij)i,j>0, une matrice stochastique infinie, irréductible et récurrente positive, elle admet donc une distribution stationnaire unique eð = (eð(j))j>0.

?
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

a

0

0

Pe =

a

a 0 a 0

0 a 0 a 0

0 0 a 0 .. . 0

0 0 a .. . a

.. 0 . 0 a

.. . a 0 a

.. 0 ... ... ... . ... 0 a 0 .

.... 0 ... ... ... ... 0 a ..

··· · · · ? · · · · · · · · · . · · · · · · ··· ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ..

Considérons »le Coin Nord-Ouest» T d'ordre N de la matrice ^Pe , TN = (Tij)i,j>0 donnécomme suit :

Tij =

^ePij,si 0 = i = N ; 0 = j = N.

.

a ? a 0 0 ? ? ? ? ? ? ? ? ? ? Tij =

a 0 a 0

0 a 0 a 0

0 0 a 0 ... 0

0 0 a ... a

0 ... 0 a

? ?????????? ... a 0

D'après l'irréductibilitéde la matrice de transition du système M/M/1,

si on considère leur Coin-Nord-Ouest, il existe au moins une ligne i pour laquelle PN j=1 T(i, j) < 0, alors la matrice tronquée TN n'est pas stochastique.

Afin de rendre T stochastique, on construit une nouvelle matrice stochastique (P(i, j))N=i,j=0 vérifiant P = T c'est a` dire P(i,j) > P^e (i,j) pour 0 = i,j = N. Cela peut se faire en utili-

sant plusieurs technique.

La masse perdue dans chaque ligne est estimée par _>k>N P(i, k). On pose pour 0 = i, j = N,

P(i,j) = Pe (i, j) + A_n(i, j) _>1 P(i, k),

k>N

avec A est une matrice stochastique quelconque, qu'on construit par des techniques d'augmentation linéaire, déjàmentionnées précédemment. En effet, on s'intéressera juste aux techniques suivantes : Augmentation de la première colonne et augmentation uniforme.

4.3 L'augmentation de la premi`ere colonne

Dans ce cas, la matrice stochastique A est donnée sous la forme suivante :

Calcul de la borne de stabilitéforte pour le cas de troncature de la ^capacité

d'attente de la file M/M/1											Page 51
1 ? 1 1 1 A = ? ? ? ? ? ? ? ? ? ? ? ? 1 1 1 1 et la matrice P devient : á ? á 0 P= ? ? ? ? ? ? ? ? ? ? á			0 0 0 0 ... ... 0 0 á 0 á 0 0	0 0 0 0 ... ... 0 0 0 á 0 á 0 0	0 0 0 0 ... ... 0 0 0 0 á 0 ... 0 0	··· ··· ··· ··· ... ... 0 0	0 0 á ... á 0	··· ··· ··· ··· ... ... 0 0	... 0 0 á	0 0 0 0 0 0 0 0	0 0 ? 0 0 0 , 0 0 ? ? ? ? ? ? ? ? ? ? ? ? 0 ? , ?????????? ... á 0
Pij =	? ? ?	^ePij, si 0 = i = N - 1 ; 0 = j = N; á, si j = N - 1 ; i = N; á, si j = 0 i = N.

4.3.1 Calcul de la borne de stabilitéforte :Augmentation de la premi`ere colonne

v- Stabilitéforte de la chaàýne de Markov X

Pour prouver la v- Stabilitéforte de la chaàýne de Markov X pour une fonction test v(k) = â^k pour â > 1, il est suffisant de trouver une mesure ó, et une fonction mesurable h sur N tels que :

a) ðh > 0, ó1I = 1, óh > 0,

b) Tij = Pij - óihi, est non négatif,

Calcul de la borne de stabilit'e forte pour le cas de troncature de la capacit'e d'attente de la file M/M/1 Page 52

c) ?ñ < 1 tel que Tõ(k) = ñõ(k), pour k ? {0,1, ..., N},

d) 1P1_õ < 8.

Pour notre cas, on choisit :

· õ(k) = â^k , â > 1 avec k ? N.

· h(i) = Pi0 :

~ 1, si i = 0;

h(i) = 1Ii=0= 0, sinon.

· ój = P0j :

ój = P0j =

? ? ?

á, si j = 0; á, si j = 1; 0, sinon.

V'erifions maintenant les conditions a), b), c) et d) :

Condition a) ðh = ð0 > 0,

ðh = ð0 = (1 - 0)/(1 - Q^N+1) > 0. (4.3)

· ó1I = á + á + 0 = 1, o`u 1I est le vecteur unit'e,

· óh = á + (0 × á) + 0 = á > 0.

Condition b) V'erifions que le noyau T est non n'egatif, on a :

T = P - h ? ó, ie T = P - {1^ereligne}

~ P0j - ój = P0j - P0j = 0, si i = 0; Tij = Pij - h(i)ój = Pij - 0 × ój = Pij, sinon,

Donc, T est un noyau non-n'egatif, ?i, j = 0 : Tij = 0.

Condition c) Montrons l'existence d'une certaine constante ñ < 1 telle que : Tõ(k) = ñõ(k), pour k = 0.

Par d'efinition,

Tõ(k) =

XN j=0

õ(j)Tkj.

Calcul de la borne de stabilit'e forte pour le cas de troncature de la capacit'e d'attente de la file M/M/1 Page 53

En effet, on a :

Pour k=0 : (Tv)(0) = Pour 1 = k = N - 1 :		XN j=0	v(j)T0j =	XN j=0	âj × 0 = 0.
(Tv)(k) =	XN j=0	v(j)Pkj = á v(k - 1) + á v(k + 1)

= á â^k-1 + á âk+1
âk{á + áâ}

= ñ1(â) v(k),

Posons

ñ1 (â) á = _â+ áâ. (4.4)

(Tv)(N) =

XN j=0

â^jPNj = v(0)PN,0 + v(N)PN,N-1

= áâ⁰ + _â^áâ^N = á + â^N{_â}

N{ á + á
_â}

âN â

= ñ2(â)v(k),

Posons

ñ2(â) = á âN + _â^á. (4.5)

On a,

á á á

ñ1(â) - ñ2(â) = _â+ áâ -

âN -

á

â

= áâ - > 0

âN

Donc, 0 < ñ2(â) < ñ1(â).

Calcul de la borne de stabilit'e forte pour le cas de troncature de la capacit'e d'attente de la file M/M/1 Page 54

Alors, il suffit de prendre ñ(â) = ñ1(â) = max{ñ1(â), ñ2(â)} verifiant :

(Tv)(k) = ñ1(â) × v(k).

Il nous reste a` demontrer que,

ñ1(â) = á â + áâ < 1,

Pour tout â > 1,

2

ñ1(â) u ëâ 1 + 0

(ë + u)â (ë + u) (1 + e)â, (4.6)

Si on suppose que pâ < 1 ? (ë/u)â < 1. Alors :

ñ(â) < 1,

En effet, on a :

1 + Qâ²

ñ(â) = (1 + Q)â^.

Pour que ñ(â) < 1 , il faut que,

(1 + 0â²) < ((1 + p)â) 1 + %â² -- â -- âp < 1

(1 -- â) + (âp(â -- 1)) < 0

(âp(â -- 1)) < (â -- 1)

âp < 1.

D'o`u, ñ(â) < 1.

Condition d) Verifions que 11P11_v < cc .

T = P -- h ? ó P = T + h ? ó

11P11_v = 11T + h ? ó11_v

= 11T 11_v + 11h11_v11ó11_v.

Par definition, on a,

11T11v = sup 0<i<N		1	XN j=0	õ(j) | Tij |
		õ(i)
= sup 0<i<N	1 õ(i)^ñõ(i)

= ñ(â) < 1.

Calcul de la borne de stabilit'e forte pour le cas de troncature de la capacit'e d'attente de la file M/M/1 Page 55

et

Ihl_v = sup õ(i)|hi| = 1,

0<i<N

1ó1v =

XN j=0

õ(j)|ój| =

XN j=0

â^jP0j

= õ(0)ó0 + õ(1)ó1 + 0 = á + áâ

= á + áâ0 < 8,

avec : â0 = sup{â : ñ(â) < 1}

Donc, 1P1_v < 8.

Ainsi, toutes les conditions sont vérifiées.

In'egalit'es de stabilit'e forte

Estimation de la d'eviation du noyau de transition

Pour pouvoir estimer numériquement l'écart entre les distributions stationnaires des états des chaines de Markov (^fX_n), (X_n), estimons au préalable la norme de déviation du noyau de transition P de la chaine de Markov de système M/M/1/8 par rapport au noyau de transition P associéa` la chaine de Markov du système M/M/1/N (modèle tronqué).

L'estimation de 1 P^e - P1_v est énoncée par le lemme suivant

Lemme 4.1 : Si p < 1 , pâ < 1 et 1 < â < â0. Alors,

1 P^e - P1_v = Ä(â) = (1â+ _N e) . (4.7)

Preuve

Par définition, on a :

e MP - PMv = sup 0<k<N		1		XN j=0		v(j)|		Pkj- - Pkj|.
		v(k)
Pour 0 = k < N - 1 : Ä0(â) = sup 0<k<N-1	1		XN j=0		v(j)|		Pkj- - Pkj| = 0.
	v(k)

Calcul de la borne de stabilit'e forte pour le cas de troncature de la capacit'e d'attente de la file M/M/1 Page 56

Pour k = N :

1 Ä1(â) = v(N)

XN j=0

v(j)|

PNj - PNj|

âN {v(0)| 1³N0 - PN0| - 1)| 1³NN-1 - PNN-1|}

1

= âN {á + 0}

á

=

âN .

On a : Ä1(â) > Ä0(â),

1 P^e - P1_v = max{Ä0(â),Ä1(â)},

Donc ;

IIP - PM_v = Ä1(â) = á âN = (1 âN A + = (â). (4.8)

D'etermination de l'erreur due a` la troncature

L'estimation de la déviation des distributions stationnaires est donn'ee par le théoreme suivant

Th'eor`eme 4.3 Soient ^-ð et ð les distributions stationnaires des chaines de Markov décrivant respectivement les états des systemes d'attente M/M/1 et M/M/1/N. Supposons que les hypotheses du Lemme 4.1 soient vérifiées. Alors, pour tout Q < 1, et sous la condition :

Ä(â) < 1 - ñ(â)

c(â) ,

nous avons l'estimation de la borne de la stabilitédans ce cas est donn'ee par :

c0(â)c(â)Ä(â)

|if - ð||_v = = Be1.

1 - ñ(â) - Ä(â)c(â)

o`u Ä(â) est défini en (4.8) et ñ(â) en (4.7) et

â(1 - 0)(1 + â0

(4.9)

c0(â) = (â - 1)(1 - Q^N+¹)(1 -

â(1 - 0(1 + â0

c(â) = 1 + (â - 1)(1 - %^N+¹)(1 - â%). (4.10)

1

Calcul de la borne de stabilit'e forte pour le cas de troncature de la capacit'e d'attente de la file M/M/1 Page 57

Preuve

Afin de d'emontrer ce r'esultat, il suffit d'estimer ||ð||_v, et ||1I||_v , o`u 1I est la fonction identiquement 'egale a` l'unit'e.

Supposons que âp < 1 , alors la norme de la distribution stationnaire peut àetre estim'ee par la formule qu est donn'ee par :

(óõ)(ðh)(óõ)(ð0)

|_v = (4.11)

1 - ñ(â) 1 - ñ(â)^.

o`u ð0 est celle obtenue pour la file d'attente M/M/1/N tronqu'ee qui est donn'ee par :

(1 - p)

ð0 = (4.12)

(1 - Q^N+¹)^.

Donc, on obtient :	á + áâ ||ð||v = 1 - (1+â2% (1+%) )		(1 - p) (1 - QN+1) (4.13)
=		â(1 - %)(1 + â%)		= c0(â). (4.14)
		(â - 1)(1 - e^N+^1)(1 - â%)

Par d'efinition, on a :

||1||_v = sup

0<k<N

âk = 1.

Donc, nous avons

c(â) = 1 + â(1 - e)(1 + âp)

(â - 1)(1 - e^N+¹)(1 - â%)^.

Ainsi, pour tout Ä(â) < ¹V⁾, nous obtenons :

c

||if - ð||_v = 0(â)c(â)Ä(â)

=

1 - ñ(â) - Ä(â)c(â) Be1.

4.4 L'augmentation uniforme

Dans ce cas, on choisit la matrice stochastiques A de telle sorte que tous ses 'el'ements sont 'egaux a` 1/N. Ainsi, la matrice P sera obtenue sous la forme :

Calcul de la borne de stabilitéforte pour le cas de troncature de la ^capacité

d'attente de la file M/M/1							Page 58
a ? a 0 P= 0 ?????????? á N	a 0 a 0 á N	0 a 0 a 0 á N	0 0 a 0 ... 0 á N	0 0 a ... a á N	0 ... . 0 a + á N	.. a á N	? ??????????

Explicitement P s''ecrire :

? ?

?

Pij =

^ePij, si 0 = i = N - 1; 0 = j = N;

N ,

á si i = N; 0 = j = N;

a+ 1 N , sii=N; j=N-1.

4.4.1 Calcul de la borne de stabilitéforte : Augmentation uniforme

õ-Stabilitéforte de la chaàýne de Markov X

De même, en suivant la même d'emarches, que celle du cas pr'ec'edent (augmentation de la premi`ere colonne), et pour le même choix de la fonction test õ, et de la fonction h et de la mesure ó, on constate que la v'erification des conditions a), b) et d) est la même. Donc, a` ce niveau on mentionnera que les 'etapes diff'erentes du cas pr'ec'edent. Ainsi :

· Montrons l'existence d'une certaine constante ñ < 1 telle que :

Tõ(k) = ñõ(k), pour k = 0?

Par d'efinition,

Tõ(k) = _XN õ(j)Tkj.

j=0

Pour k = 0 :

(Tv)(0) = _XN v(j)T0j = _XN âj × 0 = 0.

j=0 j=0

Calcul de la borne de stabilit'e forte pour le cas de troncature de la capacit'e d'attente de la file M/M/1 Page 59

Pour 1 = k = N - 1 :

(Tv)(k) =

XN j=0

v(j)Pkj = á v(k - 1) + á v(k + 1)

= á â^k-1 + á âk+1
âk{á + áâ}

= ñ1(â) v(k),

Posons alors,

á

ñ1(â) = _â+ áâ. (4.15)

Pour k = N :

(Tv)(N) =

XN j=0

â^jPNj

= v(0)PN,0 + v(1)PN,1 + v(2)PN,2 + v(3)PN,3 + ... + v(N - 1)PN,N-1 + v(N)PN,0, = â^{0 á}_N+ â^1á_N + â^2á_N + ... +â^N-1(á + á N ) +â^Ná_N,

âN á [1 1 1 á

N âN + _âN-1 +...+_â +1 + _â,

â^Ná

=

N

" â,;,'+11

â

= ñ2(â)v(N), De même, posons :

1 - (¹)^N+1

ñ2(â) = N 1 - 1+ âN+1.

{â

á

á â

1 á

ñ2(â) = 1 âá

[N(â - 1) (1 - _âN+1 ) + âN+1. (4.16)

Dans ce cas, nous constatons que : 0 < ñ2(â) < ñ1(â).

Donc, il existe une constante ñ(â) = ñ1(â) = max{ñ1(â),ñ2(â)} v'erifiant

(Tv)(k) = ñ1(â) × v(k).

Calcul de la borne de stabilit'e forte pour le cas de troncature de la capacit'e d'attente de la file M/M/1 Page 60

Nous avons dejàdemontreque si, pâ < 1 et pour tout â > 1, On a

ñ(â) = á â + áâ < 1. (4.17)

In'egalit'es de stabilit'e forte

Estimation de la d'eviation de noyau de transition Lemme 4.2 Si p < 1 et 0â < 1 et 1 < â < â0, alors

11/3- = A(â) = NâN-1(â (1 - a +

-- 1) \ fiN ^1). (4.18)

Preuve Par definition, on a : II		Pe - P1v = sup 0=k=N			1 v(k) Lv(j)| ^13kj - j=0
Pour 0 = k < N - 1 : A0(â) = sup 0=k=N-1 Pour k = N :						1	XN j=0	v(j)|	^-Pkj - Pkj| = 0.
						v(k)
1 A1(â) = v(N)	XN j=0		1 - v (j)|-13NjPNj|= âN (0)|PN0 - PN0| + v(N) + |^ePN1 - PN1|
+ v(N) + ... + |				^ePNN-1 - PNN-1| + v(N) + |						^ePNN - PNN|}

1{ á á á

= â^NN N ... + N

1 - (¹_â)^N+1

1 - ¹

â

=

+

á

âN+1

~ ~

á 1 - 1

= .

Nâ^N-1(â - 1) âN+1

On a : Ä1(â) > Ä0(â), donc;

k P^e - P k_v = max{Ä0(â), Ä1(â)}

( )

á

k P^e - P M_v = Ä1(â) = 1 - 1 = Ä(â). (4.19)

Nâ^N-1(â - 1) âN+1

.

Détermination de l'erreur due a` la troncature

L'estimation de la déviation des distributions stationnaires est donnée par le théoreme suivant

Théorème 4.4 Supposons que les hypotheses de Lemme 4.2 soient vérifiées. Alors, pour tout < 1, et sous la condition:

1 - ñ(â)

Ä(â) < c(â) ,

nous avons l'estimation de la borne de la stabilitédonnée par:

||eð - ð||_v = c0(â)c(â)Ä(â)

1 - ñ(â) - Ä(â)c(â) = Be2.

o`u Ä(â) est défini en (4.19) et ñ(â) en (4.15) et

â(1 - %)(1 + â%)

c0(â) = (â - 1)(1 - %^N+¹)(1 - â%), (4.20)

c(â) = 1 + â(1 - %)(1 + â%)

(â - 1)(1 - Q^N+¹)(1 - âQ). (4.21)

Preuve

Dans ce cas, la seule différence de la nouvelle borne due a` la même perturbation réside dans la constante qui estime la déviation entre les deux matrices de probabilités de transition.

4.4.2 Calcul de la borne reelle

La définition suivante nous permet de déterminer l'écart entre les distributions stationnaires des états des chaàýnes de Markov.

Supposons que < 1. Alors

k eðk - ðkMõ = ÓN k=0âk| eðk - ðk|,

O`u

eðk =

1 - %

1 - %N+1 ñ^k. (4.22)

avec = ë/u.

4.4.3 Bornes de deviation du nombre moyen de clients

La déviation du nombre moyen de clients pour les différentes perturbations est donnée comme suit : Si on choisit la fonction caractéristique f(s) = s (fonction identique), alors l'estimation de l'erreur due a` la troncature de la capacitéd'attente du système M/M/1 est définie par:

|ðf - eðf| = |eði - ði|_õ.kfk_õ, (4.23)

o`u

kfk_õ = ln(â) × â-[ 1

1 ln(6) ]. (4.24)

4.5 Conclusion

Dans ce chapitre, on a calculéla borne de la méthode de stabilitéforte dans le cas de la troncature de l'espace des états de la chaàýne de Markov décrivant la file d'attente M/M/1. Cette borne de perturbation est calculée de deux manières différentes : augmentation de la première colonne et augmentation uniforme. Ainsi, en considérant ces deux techniques, on peut comparer les deux bornes obtenues.

Dans le chapitre prochain, on considérera quelques exemples numériques afin de comparer ces bornes de perturbation.

5

Comparaison des techniques de troncature

Dans le chapitre pr'ec'edent, nous nous sommes int'eress'es a` l''etude th'eorique de la stabilit'e forte dans un système de files d'attente M/M/1 o`u on a consid'er'e deux techniques de troncature. Nous avons pu exhiber les conditions suffisantes de la stabilit'e forte li'ees au système. Dans ce chapitre, nous nous int'eresserons a` l'aspect pratique du problème. Pour ce faire, nous avons 'elabor'e un algorithme qui permet d'estimer les deux bornes de perturbation obtenues dans le chapitre pr'ec'edent, et de v'erifier les conditions ainsi que la d'etermination de leurs domaine de stabilit'e optimal. Enfin, une comparaison entre les deux bornes obtenues et la borne r'eelle sera effectu'ee.

5.1 Applications numériques

Dans cette section, nous pr'esentons quelques r'esultats num'eriques qu'on obtient par application de l'algorithme de stabilit'e forte, sous l'environnement Matlab et ce tout en consid'erant les deux techniques de troncature de l'espace des 'etats de la chaàýne de Markov d'ecrivant la file d'attente M/M/1.

5.1.1 Environnement MATLAB

Notre choix s'est port'e sur l'utilisation de l'environnement MATLAB qui nous permet, gràace a` la richesse de sa bibliothèque math'ematique, d'optimiser les instructions dans les programmes r'ealis'es dans le cadre de ce travail. En effet, MATLAB est un système interactif et convivial de calcul num'erique et de visualisation graphique destin'e aux ing'enieurs et

scientifiques qui possède un langage de programmation a` la fois puissant et simple. De plus, il intègre des fonctions d'analyse numérique, de calcul matriciel, etc.

5.1.2 Approche algorithmique

Nous avons élaboréun algorithme qui permet d'estimer les deux bornes de perturbation présentées précédemment, et de vérifier les conditions, ainsi que la détermination de leur domaine de stabilitéoptimal.

5.1.3 Algorithme de StabilitéForte

'ETAPE 1

- Introduire le nombre de troncature N;

- Introduire le taux d'arrivées A;

- Introduire le taux de service u ;

- Introduire le pas h.

'ETAPE 2

- Déterminer 30, en construisant un intervalle I1 = [1 + h, 30], o`u 30 est le réel 3 > 1 vérifiant la condition p(3) < 1.

- Déterminer un sous intervalle I2 = [3min, 3max] ? I1, pour lequel Ä < 1-ñ(â)

c(â) soit vérifiée

'ETAPE 3

- Déterminer une valeur optimale de 3 noté3opt ? I2 qui minimise la valeur de l'erreur.

'ETAPE 4 - Fin.

5.1.4 Organigramme de stabilitéforte

Les différentes étapes de notre algorithme peuvent être présentées dans un organigramme suivant :

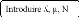
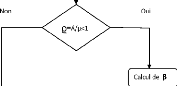
FIGURE 5.1 - Organigramme de l'algorithme

Comparaison des résultats et discussion

* Afin de comparer les résultats obtenus des deux bornes de stabilitéforte par les deux techniques de troncature, nous implémentons l'algorithme pour les différentes valeurs du niveau de la troncature pour laquelle une valeur optimale _âopt sera calculée.

* La même valeur de _âopt sera considérée afin de comparer ces deux techniques de troncature et d'évaluer la borne réelle.

* Nous avons implémenténotre algorithme pour une valeur de la charge de système = 0.25 et l'exécution de cet algorithme avec un pas h = 0.01 nous permet d'obtenir les résultats représentés dans des tableaux suivants :

5.1.5 Variation de l'erreur en fonction de %

D'après les résultats obtenus, nous pouvons constater le domaine de stabilitéliéau différentes valeurs de , la borne _âmax atteint son maximum ensuite elle diminue progressivement lorsque le paramètre prend de petites valeurs comme le montre le tableau suivant (par exemple pour N = 15).

Q	âmin	âmax	âopt	SSBP	SSBU
0.1	1.0100	9.9900	8.3273	1.4477e - 012	1.0968e - 013
0.25	1.0100	3.9900	3.3602	4.6188e - 006	4.3839e - 007
0.4	1.0100	2.4900	2.1268	0.0130	0.0016
0.5	1.0100	1.9800	1.7242	0.6987	0.1070
0.6	-	-	-	-	-

TABLE 5.1 - Tableau des variations de l'erreur en fonction de Q

C'est pour cela que notre choix se portera sur la valeur Q = 0.25 et N > 4 pour la suite de l'application, et le graphe suivant illustre qu'àl'augmentation de Q, l'erreur augmente et elle tend vers l'infinie a` partir de Q > 0.6.

FIGURE 5.2 - Graphe des erreurs Be1 et Be2 : en fonction de Q

5.1.6 Variation de l'erreur en fonction de N

Approximation de la d'eviation des distributions stationnaires et l'approximation du nombre moyen de clients dans le système

1er Cas : Augmentation de la premi`ere colonne :

L'implémentation de l'algorithme dans ce cas permet d'obtenir les résultats pour la technique d'augmentation de la premi`ere colonne représentés dans le tableau suivant :

% = 0.25	\	||eð -ð||v		|eðf - ðf|
N	âopt	SSBP	Re'el	SSBP	Re'el
5	2.7134	0.3974	0.2711	0.1465	0.0999
6	2.8189	0.1381	0.1994	0.0490	0.0708
7	2.9144	0.0475	0.1669	0.0163	0.0574
8	2.9983	0.0160	0.1472	0.0054	0.0493
9	3.0716	0.0053	0.1335	0.0017	0.0438
10	3.1356	0.0017	0.1209	0.0005	0.0389
11	3.1918	5.3593e-004	0.1112	0.0002	0.0352
12	3.2415	1.6658e-004	0.0988	0.0001	0.0309
13	3.2855	5.1037e-005	0.0901	0.0000	0.0279
14	3.3249	1.5440e-005	0.0755	0.0000	0.0231
15	3.3602	4.6188e-006	0.0672	0.0000	0.0204
16	3.3921	1.3680e-006	0.0510	0.0000	0.0154
17	3.4210	4.0155e-007	0.0437	0.0000	0.0131
18	3.4473	1.1692e-007	0.0284	0.0000	0.0084
19	3.4714	3.3796e-008	0.0233	0.0000	0.0069
20	3.4935	9.7044e-009	0.0120	0.0000	0.0035
21	3.5138	2.7697e-009	0.0094	0.0000	0.0028
22	3.5326	7.8610e-010	0.0034	0.0000	0.0010
23	3.5500	2.2197e-010	0.0025	0.0000	0.0007
24	3.5661	6.2384e-011	4.7730e-004	0.0000	0.0001
25	3.5812	1.7456e-011	3.3040e-004	0.0000	0.0001
26	3.5952	4.8648e-012	0	0.0000	0
27	3.6084	1.3506e-012	0	0.0000	0
28	3.6207	3.7366e-013	0	0.0000	0
29	3.6323	1.0303e-013	0	0.0000	0
30	3.6431	2.8324e-014	0	0.0000	0

TABLE 5.2 - Tableau des erreurs Be1 : l'augmentation de la premi`ere colonne

Même remarque que celle de la variation de , mais dans ce cas c'est le contraire. Le fait que l'augmentation de la valeur du N induit une diminution de l'erreur commise comme le montre le tableau ci-dessus.

Ceci est illustr'e par le graphe suivant :

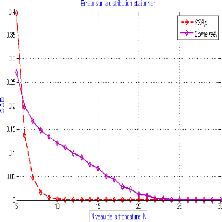
FIGURE 5.3 - Graphe des erreurs Be1 : avec l'augmentation de la premi`ere colonne

Pour l'approximation du nombre moyen de clients dans le système

On peut s'int'eresser a` des caract'eristiques pr'ecises, dans le but d'avoir une id'ee sur la pr'ecision des r'esultats. Dans cette partie, nous nous int'eressons au nombre moyen de clients dans le syst`eme. Les r'esultats obtenus sont ainsi repr'esent'es dans le tableau pr'ec`edent. Et ceci peut être illustr'e par le graphe suivant :

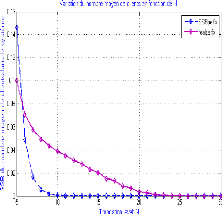
FIGURE 5.4 - Graphe de variation du nombre moyen de clients en fonction de N

On voit que le nombre moyen de clients dans le système original (tronqué) est inférieur a` celui du système étudiéM/M/1/N (idéal) pour N < 9. De plus, l'augmentation du N induit une diminution de l'erreur sur le nombre moyen de clients a` partir de N > 12 et pour âopt ? [3.2855, 3.6431] le nombre de clients dans le système est nul.

2er Cas Augmentation uniforme :

Même comportement que le premier cas, mais il y a une amélioration de la valeur de l'erreur obtenue par la technique d'augmentation uniforme et les résultats sont donnés dans le tableau suivant :

% = 0.25	\	||eð -ð||v		|eðf - ðf|
N	âopt	SSBU	Re'el	SSBU	Re'el
5	2.7134	0.1203	0.2711	0.0443	0.0999
6	2.8189	0.0351	0.1994	0.0125	0.0708
7	2.9144	0.0103	0.1669	0.0035	0.0574
8	2.9983	0.0030	0.1472	0.0010	0.0493
9	3.0716	8.6730e-004	0.0003	0.0003	0.0438
10	3.1356	2.4898e-004	0.1209	0.0001	0.0389
11	3.1918	7.0947e-005	0.1112	0.0000	0.0352
12	3.2415	2.0075e-005	0.0988	0.0000	0.0309
13	3.2855	5.6437e-006	0.0901	0.0000	0.0279
14	3.3249	1.5772e-006	0.0755	0.0000	0.0231
15	3.3602	4.3839e-007	0.0672	0.0000	0.0204
16	3.3921	1.2124e-007	0.0510	0.0000	0.0154
17	3.4210	3.3377e-008	0.0437	0.0000	0.0131
18	3.4473	9.1497e-009	0.0284	0.0000	0.0084
19	3.4714	2.4985e-009	0.0233	0.0000	0.0069
20	3.4935	6.7981e-010	0.0120	0.0000	0.0035
21	3.5138	1.8436e-010	0.0094	0.0000	0.0028
22	3.5326	4.9840e-011	0.0034	0.0000	0.0010
23	3.5500	1.3436e-011	0.0025	0.0000	0.0007
24	3.5661	3.6123e-012	4.7730e-004	0.0000	0.0001
25	3.5812	9.6876e-013	4.7730e-004	0.0000	0.0001
26	3.5952	2.5920e-013	0	0.0000	0
27	3.6084	6.9201e-014	0	0.0000	0
28	3.6207	1.8437e-014	0	0.0000	0
29	3.6323	4.9026e-015	0	0.0000	0
30	3.6431	1.3013e-015	0	0.0000	0

TABLE 5.3 - Tableau des erreurs Be2 : Augmentation uniforme

Ceci est illustrepar le graphe suivant :

FIGURE 5.5 - Graphe des erreurs Be2 : l'augmentation uniforme

Pour l'approximation de l'erreur sur le nombre moyen de clients dans le système

On voit bien que l'erreur sur le nombre moyen de client dans le système ideal est inferieur a` celui du nombre moyen de clients dans le système reel pour N < 10, et a` partir de N > 10, le nombre est nul.

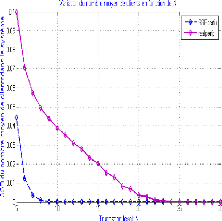
FIGURE 5.6 - Graphe de variation de l'erreur sur le nombre moyen de clients en fonction de N

Interprétation des résultats

L'application numérique de la technique de troncature sur la capacitéde la file d'attente, nous a permis d'observer le comportement de l'erreur relative aux deux bornes obtenues par les deux techniques de troncature. Il est alors aiséde constater d'apres ces deux approches que la borne obtenue par l'augmentation uniforme est meilleure par rapport a` celle obtenue par l'augmentation de la premiere colonne.

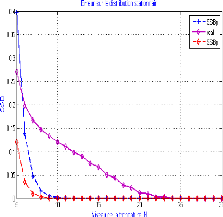
FIGURE 5.7 - Graphe comparatif des erreurs Be1 et Be2

D'après ce graphe, nous pouvons constater que l'erreur obtenue par l'augmentation uniforme est plus petite que celle de l'augmentation de la première colonne, et celle de l'erreur réelle, et a` partir de N = 26 toutes les erreurs sont nulles, ce qui signifie que les deux modèles (originale et tronqué) coincident.

Pour l'approximation de l'erreur sur le nombre moyen de clients dans le système

FIGURE 5.8 - Graphe comparatif de variation de l'erreur sur le nombre moyen de clients en fonction de N

3	SSBP	SSBU
2	0.9344	0.3268
2.3	0.5205	0.1712
2.7	0.3975	0.1206
2.7134	0.3974	0.1203
2.769	0.3994	0.1197
2.9	0.4209	0.1232

TABLE 5.4 - Tableau des variations de l'erreur en fonction de 3

5.1.7 Variation de l'erreur en fonction 3

Pour N = 5 et = 0.25, on a

L'erreur sur la distribution stationnaire par augmentation uniforme SSBU qui est obtenue pour 3opt = 2.7690 est SSBU = 0.1197, et l'erreur obtenue pour 3opt = 2.7134 par augmentation de la première colonne est SSBP = 0.3974.

Donc, d'après ce tableau, on peut bien comparer les résultats obtenus par les deux techniques par la variation de 3. Ainsi, l'erreur obtenue par la technique d'augmentation uniforme est plus petite que celle obtenue par l'augmentation de la première colonne. Alors ,la croissance de 3 entraàýne une diminution de l'erreur.

5.2 Conclusion

Après l'étude théorique de l'applicabilitéde la méthode de stabilitéforte dans le système M/M/1/N, dans ce chapitre, nous avons pu réaliser une application numérique dans le cas de la troncature de la capacitéde la file d'attente de ce système, tout en exploitant les résultats présentés dans le quatrième chapitre.

Le but de cette troncature est d'analyser la qualitédes bornes de stabilitéforte via les deux techniques, et cela ce réalise quand la charge de système < 1. On remarque dans tous les cas que la perturbation effectuée sur les paramètres introduits, les erreurs obtenues par la technique d'augmentation uniforme est meilleure que celle d'augmentation de la première colonne et ces erreurs obtenues par les deux techniques tendent vers zero quand N tend vers l'infini.

On remarque ainsi, dans le cas o`u la charge de système est proche de 1, que la condition d'optimalitén'est pas vérifiée et on conclut que le système devient instable d'o`u l'inutilitéde l'application de la méthode stabilitéforte a` ce niveau.