IV. 1. 1. 2. TEST
STATISTIQUE
Un test statistique est un ensemble de procédés
susceptibles d'aboutir à un jugement `` impartial et donc
inattaquable''. Pour cela, tout test statistique est lié à un
intervalle de confiance dont le résultat consiste à
déterminer laquelle parmi deux décisions possibles est la
meilleure dans une situation donnée.
La construction d'un test statistique n'est rien d'autre que
la détermination de la région critique. Cette
détermination se fait sans connaître le résultat de
l'expérience, et donc à priori. Le test est aussi un moyen
rationnel de trancher un problème en optant pour une décision par
rapport à une autre, et ce en connaissance du risque encouru (NTOMBI,
2007 ; SAPORTA, 1990).
Pour tester l'évolution pluviométrique
notamment, nous considérons deux hypothèses :
- la première est Ho, l'hypothèse
nulle qui stipule que la distribution de la pluviométrie sur le bassin
(Bandundu) n'a pas connue un changement significatif depuis 39 ans ;
- la deuxième est H1, l'hypothèse
alternative qui stipule le contraire.
Nous avons choisi le test de Laplace-Gauss ou
loi normale qui est un outil indispensable à l'analyse et à
l'interprétation des données obtenues par l'observation ou
l'expérience (DONALD & al., 1992).
Pour analyser ces données, nous
considérons :
- Ho : la normale établie dans les
Atlas climatiques du bassin Congolais
par F.BULTOT en 1971.
- La moyenne calculée de 39 ans : 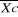 = 1490,6mm/an = 1490,6mm/an
- L'écart - type S = 220,3mm (F. BULTOT, 1971)
Si Ho est vrai, l'expérience ayant
porté sur n = 39 est donc que :
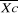 doit suivre une loi de L.G. (m(HO) , doit suivre une loi de L.G. (m(HO) , 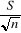 ) ou que ) ou que 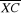 L. G. (1600, L. G. (1600, 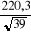 ) )
- a un seuil K qui n'a que 5 chances sur 100 d'être
dépassée,
En d'autre terme, on aura que L.G. (ì ; ó)
englobe L.G. (ì +/-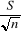 ) )
K (Ho) = m(Ho) +/- 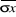 . Tá/2 . Tá/2
Avec : - 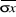 = = 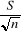 : erreur - type de la moyenne : erreur - type de la moyenne
- Tá/2 : est la valeur
tabulée de la moyenne au seuil correspondant dans la loi normale
réduite (Tá/2 = 1,6449). Cette valeur tabulée
est tirée dans la table de la loi normale centrée réduite
qui sert à déterminer les probabilités de n'importe quelle
distribution normale (DONALD & al., 1992).
- á = seuil
Pour L.G. (ì +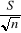 ) ; K (Ho) = 1600 + 35,3 x 1,6449 = 1658,1mm ) ; K (Ho) = 1600 + 35,3 x 1,6449 = 1658,1mm
Pour L.G. (ì -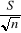 ) ; K (Ho) = 1600 - 35,3 x 1,6449 = 1541,9mm ) ; K (Ho) = 1600 - 35,3 x 1,6449 = 1541,9mm
En comparant la moyenne calculée (1490,6mm/an) et les
seuils des régions critiques de K (Ho) 1658,1mm et
1541,9mm ; nous constatons que 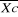 est inférieur à K (Ho), donc nous sommes
enclin de retenir H1 qui confirme que la distribution de la
pluviométrie a connu un changement significatif dans le sens d'une
baisse depuis 39 ans. est inférieur à K (Ho), donc nous sommes
enclin de retenir H1 qui confirme que la distribution de la
pluviométrie a connu un changement significatif dans le sens d'une
baisse depuis 39 ans.
Ce constat vient confirmer le propos des enquêtés
sur la diminution de la pluviométrie actuelle et la récurrence
des pluies souvent sous forme d'orage.
Ces orages qui ne sont pas favorables à la recharge des
aquifères du bassin versant, mais plutôt favorables au
ruissellement et au ravinement, détruisent de plus en plus des
habitations et tuent des êtres humains à chaque saison des
pluies.
| 


