IV. 3. 1. 2. TEST DE
MOYENNE
Pour être au moins concis sur cette prise de position
quant à la diminution des pluies dans la région de Kikwit,
faisons appel au test de moyenne. Ce test se calcule par :
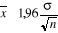
Avec  : écart type de la série (311,6mm) : écart type de la série (311,6mm)
n : la taille de l'échantillon (37)
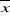 : moyenne de la série (1299,8mm) : moyenne de la série (1299,8mm)
ì : la normale établie par BULTOT (valeur
à comparer avec ce test)
- Lorsque ì est inférieur à 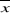 +1,96 +1,96 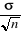 ( (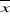 supérieur), il y a alors présomption
d'augmentation plausible significative des pluies ; supérieur), il y a alors présomption
d'augmentation plausible significative des pluies ;
- Lorsque ì est supérieur à 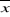 -1,96 -1,96 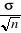 ( (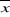 inférieur), il y a dans ce cas présomption de
diminution plausible significative des pluies. inférieur), il y a dans ce cas présomption de
diminution plausible significative des pluies.
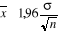 = = 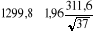
Pour 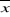 supérieur = 1299,8 + 100,4 = 1400,2mm supérieur = 1299,8 + 100,4 = 1400,2mm
Pour 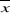 inférieur = 1299,8 - 100,4 = 1199,4mm inférieur = 1299,8 - 100,4 = 1199,4mm
La normale établie par BULTOT (ì=1600mm)
étant supérieure au deux cas c'est - à - dire 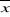 supérieur et supérieur et 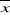 inférieur, la décision est la
présomption plausible de diminution significative des pluies à la
station de Kikwit. Cette présomption de diminution des pluies vient
renforcer les analyses faites un peu plus haut sur cette station. inférieur, la décision est la
présomption plausible de diminution significative des pluies à la
station de Kikwit. Cette présomption de diminution des pluies vient
renforcer les analyses faites un peu plus haut sur cette station.
IV. 3. 2. EVAPORATIONS
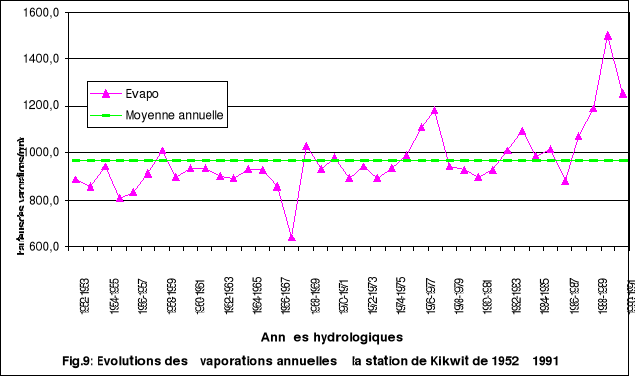
En suivant l'évolution de la courbe des
évaporations à Kikwit par rapport à celle de la moyenne
annuelle, elle présente une tendance à la hausse. Une
augmentation graduelle des évaporations sur l'ensemble de la
série.
IV. 3. 3. ANALYSE
COMPARATIVE DES PARAMÈTRES PLUIES ET EVAPORATIONS
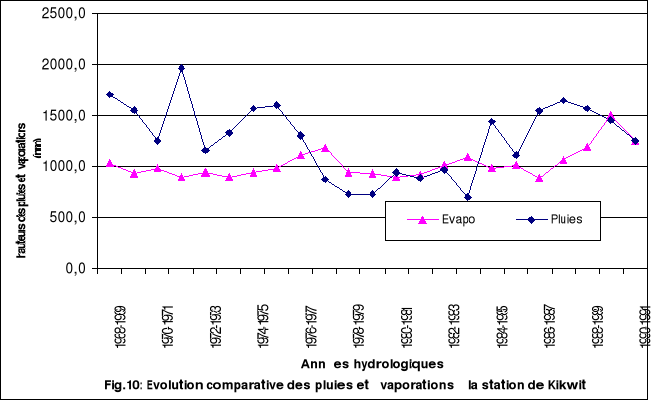
Les analyses faites sur les deux paramètres
séparément ont montré une tendance à la hausse
à la station météorologique de Kikwit. Nous pouvons les
constater dans la tranche 1972-1973 jusqu'en1975-1976 et plusieurs d'autres
années sur ce graphique. Pour confirmer cette évolution
couplée, nous faisons appel au test de corrélation de BRAVAIS
PEARSON.
IV. 3. 3. 1 : TEST DE
CORRELATION DE BRAVAIS PEARSON
Sur un échantillon n de 23 ans ou les pluies et les
évaporations se couplent, nous pouvons calculer l'écart type, la
covariance et ensuite le coefficient de corrélation.
COV(x,y) =  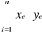 et rx,y = et rx,y = 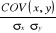
La moyenne de la série des pluies 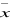 = 1274mm = 1274mm
La moyenne de la série des évaporations 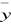 = 1025,7mm = 1025,7mm
L'écart type de la série des pluies
óx = 354,9mm
L'écart type de la série des évaporations
óy = 145,9mm
COV(x,y) =  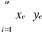
COV(x,y) = 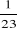 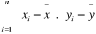 = 1641,2 = 1641,2
rx,y = 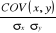
rx,y = 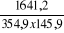 = 0,032 = 0,032
Le test proprement dit va nous permettre de trancher sur la
linéarité de la corrélation entre les pluies et les
évaporations à la station de Kikwit:
tc = 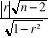
avec (n-2) : degré de liberté
tc : valeur calculée du
test qui représente Ho
r : coefficient de corrélation
r2 : coefficient de
détermination
n : effectif
tc = 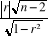 = = 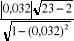 = 0,1466424/0,998979 = 0,1467927 = 0,1466424/0,998979 = 0,1467927
Au seuil á qui n'a que 5% de chance de se tromper, on
peut calculer la valeur tabulée H1 :
tt(0,05 ; n-2)
tt (0,05 ; 21) = 0,4132
Sur ce, tt (valeur tabulée)
étant supérieur à tc (valeur
calculée) (tt > tc ), l'hypothèse
alternative (H1) est rejetée et on retient l'hypothèse
nulle (Ho). Elle justifie cette parfaite évolution
concordante qui existe entre les pluies et les évaporations dans la
région de Kikwit et ses environs.
| 


