V. 2. APPROCHE
QUANTITATIVE
Nous faisons appel aux lois statistiques pour l'étude
des valeurs hydrologiques extrêmes. Concrètement, nous utilisons
la loi de GOODRICH et celle de GUMBEL. Ces lois consistent à
déterminer les périodes de récurrence de certaines valeurs
à partir de la mesure limnimétrique (NTOMBI, 2007 ;
MUZY A. & HIGY C., 1998 ; DUBAND. D., 1982 ; MEYLAN P., MUZY
A., 1999).
L'on peut aussi, avec ces lois arriver à prévoir
les inondations des certaines localités riveraines qui sont souvent
menacées par cette catastrophe, en sommant tout simplement ces
récurrences calculées avec leur niveau zéro de
l'échelle d'étiage (MBOKOLO, 2003).
V.
2. 1. METHODE DE GOODRICH
V. 2. 1. 1. PRESENTATION
THEORIQUE
Cette loi appartient à la famille des lois
exponentielles généralisées.
Sa fonction densité est la suivante :
F (H) = 1 - eA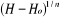
Cette loi comporte trois paramètres d'ajustement,
à savoir :
- A : est le paramètre de l'échelle, voir S
de la loi de GUMBEL,
soit S = 1/a = 0,780 ó
- Ho : est le débit initial ou
débit ordinaire,
- n : est le paramètre de forme,
déterminé à partir de l'expression ö(n),
- H : est le débit inconnu ou recherché.
Il faut savoir que les valeurs de ö(n) ont
été tabulées pour en déduire la valeur de n
jusqu'au millième près, au besoin par interpolation
linéaire. Ainsi GOODRICH a établi le tableau suivant :
Tableau 5 : Valeurs de n correspondant à
ö(n)
|
n
|
0,30
|
0,35
|
0,40
|
0,45
|
0,50
|
0,55
|
0,60
|
0,65
|
0,70
|
0,75
|
0,80
|
0,85
|
0,90
|
0,95
|
1,00
|
|
ö(n)
|
0,069
|
0,217
|
0,359
|
0,496
|
0,631
|
0,764
|
0,896
|
1.028
|
1,160
|
1,294
|
1,430
|
1,567
|
1,708
|
1,852
|
2.000
|
V. 2. 1. 2. SCHEMA GENERAL DES
OPERATIONS
V. 2. 1. 2. 1.
CALCUL DES PARAMETRES EMPIRIQUES DE L'ECHANTILLON
a) 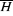 = 2,54 m = 2,54 m
b) ó = 0,31057345 m
V. 2. 1. 2.
2. CALCUL DES INTERMEDIAIRES
a) Moment centré : M3
= 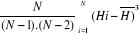
avec N la taille de l'échantillon
M3 = 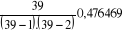 = 0,0132164 = 0,0132164
b) Le paramètre forme ö(n) =
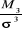 = 0,0132164/(0,31057345)3 = 0,0132164/(0,31057345)3
ö(n) =
0,4410713
c) Détermination de n : en nous
référant au tableau n°4, ö(n) est compris entre les
valeurs 0,359 et 0,496.
Pour ö(n) = 0,359 ; n = 0,40
Pour ö(n) = 0, 496 ; n = 0,45
Par la méthode d'extrapolation :
0,359  0,40 0,40
0,137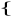 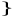 0,05 0,05
0,496  0,45 0,45
Ainsi 0,137  0,05 0,05
1  0,05 / 0,137 = 0,3649635 0,05 / 0,137 = 0,3649635
La différence entre ö(n) calculé
0,4410713 et la valeur tabulée minimale 0,359 est égal à
0,0821 ; alors 0,0821  0,05 x 0,0821 / 0,137 = 0,0299635 = 0,03 0,05 x 0,0821 / 0,137 = 0,0299635 = 0,03
 la valeur de n sera alors : 0,03 + 0,40 = 0,43 la valeur de n sera alors : 0,03 + 0,40 = 0,43
Lorsque la différence est faite avec la valeur
tablée maximale ; n est égal à : 0,45 -
(0,05 x 0,05493 / 0,137) = 0,4299525 = 0,43
c) Calcul des intégrales d'EULER
(x)
1 = (n + 1) = (0,43 + 1) = (1,43) = 0,88604
2 = (2n + 1) = (1,86) = 0,94869
3 = (3n + 1) = (2,29) = 1,87224
Il faut noter que 1, 2 et 3
sont des valeurs lues dans la table d'EULER (table en annexe), et le cas
échéant, déterminées par extrapolation.
d) Détermination de Ho et A
Ho = 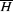 - - 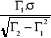 = 2,54 - = 2,54 - 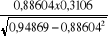 =2,54- 0,275204024/0,4045035 =2,54- 0,275204024/0,4045035
Ho = 1,8596498
A = 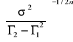 = = 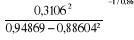 = = 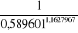 = 1/0,54101 = 1/0,54101
A = 1,8483947 = 1,85
e) La densité de fonction : F (H)
= 1 - e -A 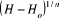
Dans cette fonction F(H), H reste la seule
donnée inconnue, c'est - à - dire la limnimétrie qui
représentera la récurrence à n années reproduite ou
à reproduire.
F(H) = 1 - e -1,85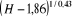
|
|



