III.4 QUELQUES EXEMPLES [6]
Exemple 3. 4. 1 soit à résoudre dans 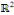 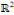 l'EDP suivante : l'EDP suivante :
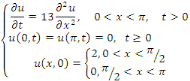
D'après le résultat de l'EDP de la chaleur
intégrée au point 3.2, dans le cas des conditions aux limites du
type DIRICHLET avec 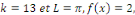 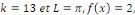 la solution est donnée par l'expression la solution est donnée par l'expression
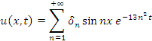
Alors, calculons les coefficients de Fourier 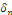 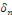 sachant que sachant que 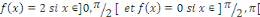 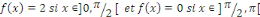
Les coefficients de Fourier sont donnés par :
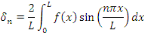
Dans le cas où 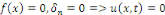 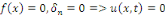 une solution triviale. une solution triviale.
Considérons le cas où 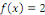 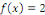
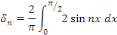
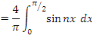
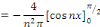
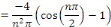
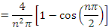
D'où la solution :
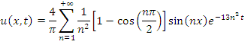
Exemple 4. 2 considérons dans 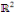 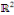 l'EDP suivante : l'EDP suivante :
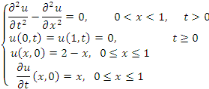
D'après le résultat du problème d'Ondes
au point 3.3. avec 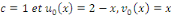 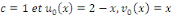 la solution est donnée par : la solution est donnée par :
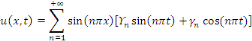
Etant une série de Fourier, calculons les coefficients
de Fourier 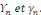 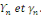
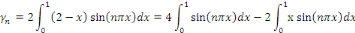
Posons  
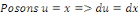
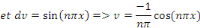
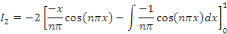
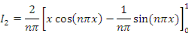

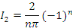
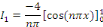
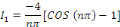
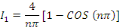
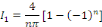
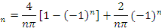
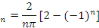
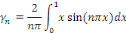
Posons 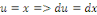 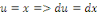 et et 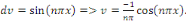 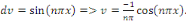
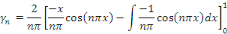
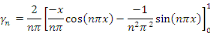
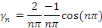
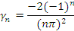
D'où la solution
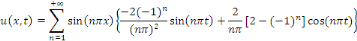
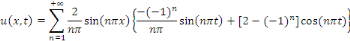
Exemple 3. 4. 3 soit à résoudre dans 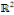 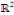 l'EDP : l'EDP :
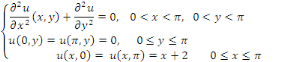
D'après le résultat de l'EDP de Laplace avec
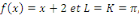 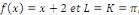 la solution est donnée par l'expression : la solution est donnée par l'expression :
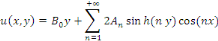
Calculons alors les coefficients de Fourier 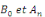 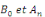 : :
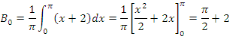
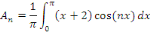
Par la méthode de changement de variable, posons 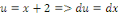 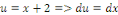
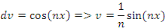
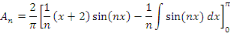
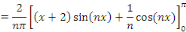
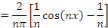
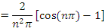
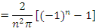
D'où la solution générale
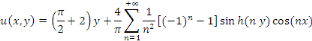
| 


