III.2. EQUATION DES ONDES
L'équation des ondes sur l'intervalle [0, L] avec 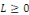 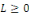 dans dans 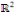 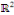 est donnée par est donnée par

INTEGRATION DU PROBLEME
En fait, par la méthode de Fourier, posons
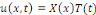
Et portons dans 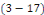 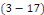 , l'équation devient : , l'équation devient :

Comme nous cherchons des solutions non triviales
identiquement, alors il existe 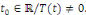 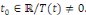 Par conséquent, nous obtenons le système Par conséquent, nous obtenons le système

Car les membres de gauche et de droite dépendent des
variables indépendantes 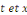 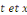 respectivement. C'est-à-dire que respectivement. C'est-à-dire que 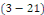 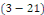 est constante (il existe est constante (il existe 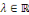 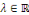 ) )
Avec les conditions aux limites, on cherche les solutions non
nulles de 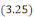 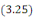 : :
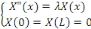
Les solutions dépendent de la constante 
1er CAS : si 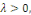 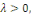 alors alors
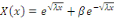
En tenant compte des conditions aux limites, la solution
vient :
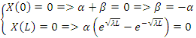
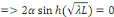
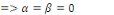
Il n'y a pas de solutions non nulles dans ce cas.
2ème CAS : si 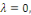 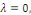 alors alors
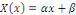
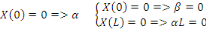
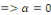
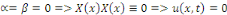
Pour tout 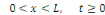 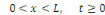 c'est-à-dire il n'y a pas de solution non nulles dans ce cas. c'est-à-dire il n'y a pas de solution non nulles dans ce cas.
3ème CAS : si 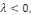 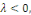 alors alors
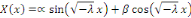
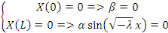
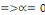 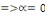 ou bien ou bien 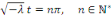 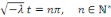
Il existe donc des solutions non nulles dans ce cas qui
sont :
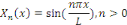
Associées aux valeurs propres de 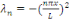 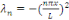
Au total, on a obtenu une suite infinie de solutions
associées chacune à une valeur de 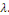 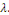 On appelle les solutions On appelle les solutions 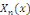 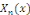 les fonctions propres du problème et les les fonctions propres du problème et les 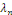 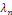 les valeurs propres associées. les valeurs propres associées.
La fonction propre, comme les vecteurs propres en
algèbre linéaire, est définie à un scalaire
multiplicatif près.
Le produit scalaire
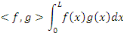
orthogonalise toujours la suite des 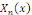 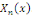
Si 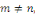 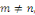
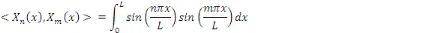
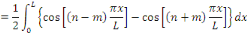

Si 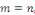 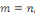
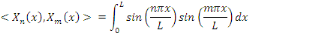
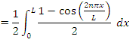
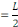
On résout l'équation 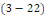 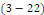 pour les valeurs de pour les valeurs de 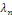 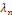 trouvées précédemment et sans se préoccuper
de la condition initiale. trouvées précédemment et sans se préoccuper
de la condition initiale.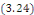 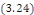 a pour solution lorsque a pour solution lorsque 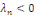 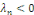 . .
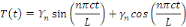
Comme il n'y a pas de conditions initiales à cette EDO
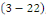 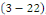 nous trouvons un espace vectoriel de dimension 2 de solutions nous trouvons un espace vectoriel de dimension 2 de solutions
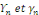 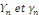 sont des conditions arbitraires. sont des conditions arbitraires.
A ce stade, les fonctions
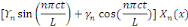
Sont solutions de 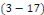 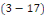 et des conditions aux limites et des conditions aux limites 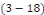 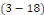 et et 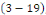 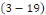
Mais pas de condition initiale.
Réécrivons la solution 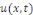 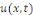 comme somme de toutes les solutions élémentaires (par
principe de superposition). comme somme de toutes les solutions élémentaires (par
principe de superposition).
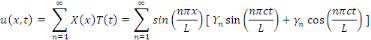
Où 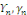 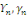 sont des constantes arbitraires. sont des constantes arbitraires.
Déterminons maintenant les coefficients 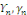 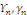 grâce aux conditions initiales grâce aux conditions initiales 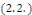 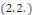
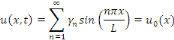
Les constantes 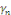 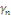 peuvent donc s'interpréter comme étant les
coordonnées de la décomposition de peuvent donc s'interpréter comme étant les
coordonnées de la décomposition de 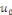 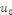 dans la base dans la base 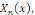 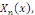 soit soit
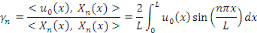
Quant à la condition 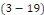 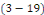 elle donne elle donne
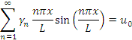
Nous obtenons donc
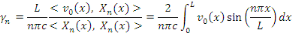
III.3 EQUATION DE LAPLACE
L'équation de Laplace dans 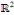 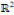 est donnée par : est donnée par :
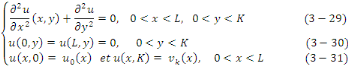
Par cette méthode, on pose toujours 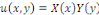 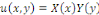 où où 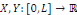 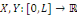 sont fonctions données. sont fonctions données.
Dans ce cas, les conditions de comptabilité
sont :
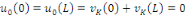
En remplaçant 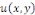 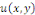 par par 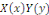 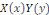 dans l'équation dans l'équation 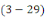 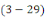 , on obtient , on obtient
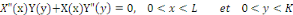
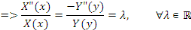
Et donc, il y a une constante ë telle que :
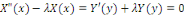
La condition devient : 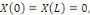 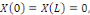 si non si non 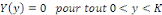 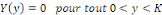
Cherchons les valeurs propres et les fonctions propres du
problème aux limites :
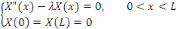
Nous trouvons que le spectre est 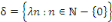 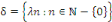
Où 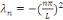 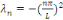
Et une fonction propre associée à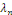 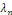 est est
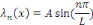
Pour 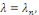 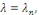 la solution générale de la solution générale de
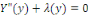
Est 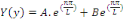 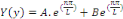
Où A et B sont des constants arbitraires.
Les solutions de 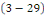 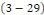 sont : sont :
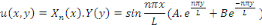
Est une solution générale de l'équation
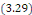 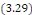 quelque soit N?N et les coefficients quelque soit N?N et les coefficients 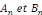 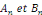 . .
Essayons de choisir N, 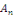 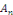 et et 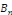 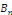 afin de satisfaire les conditions aux limites qui deviennent : afin de satisfaire les conditions aux limites qui deviennent :
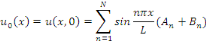
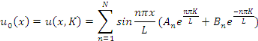
Ceci montre formellement
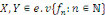
Dans ce cas, on peut déterminer N, 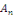 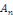 et et 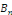 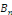 de la manière suivante : de la manière suivante :
Si 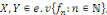 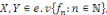 nous pouvons écrire : nous pouvons écrire :
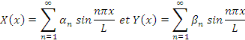
Où tous, sauf le nombre fini, les coefficients 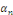 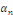 et et 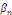 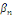 sont nuls. sont nuls.
Nous calculons en multipliant par 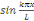 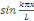 et intégrons entre 0 et L. et intégrons entre 0 et L.
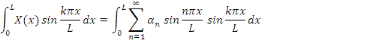
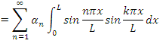
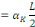
De même façon,
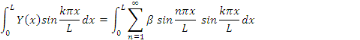
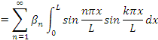
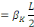
Donc, il suffit de choisir 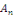 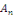 et et 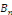 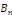 tels que tels que
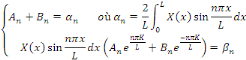
Où 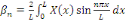 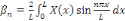
La solution su système est :
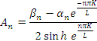
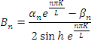
La méthode de Fourier nous a permis donc de
résoudre le problème pour des fonctions 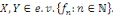 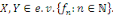
Dans ce cas, la solution du problème sous forme de
séries de Fourier est :
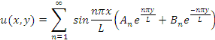
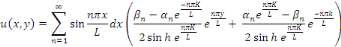
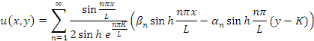
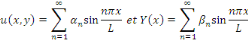
L'hypothèse que 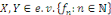 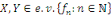 assure seulement qu'un nombre fini de constantes assure seulement qu'un nombre fini de constantes 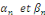 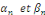 sont nuls et donc il s'agit des sommes. sont nuls et donc il s'agit des sommes.
Notons que la solution vérifie les conditions de
comptabilité et est infiniment dérivable.
| 


