CHAPITRE III : APPLICATION DES SERIES DE FOURIER A
L'INTEGRATION DE QUELQUES EDP LINEAIRES DU SECOND ORDRE.
III.1. METHODE DE SEPARATION DES VARIABLES
La méthode de séparation des variables,
communément appelée de Fourrier, est largement utilisée
aux EDP. Elle consiste à chercher des solutions particulières de
la forme 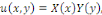 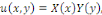 où X et Y sont des fonctions en x et y respectivement. Dans des
nombreux cas, l'EDP se réduit à deux équations
différentielles ordinaires pour X et Y. on obtient donc des
problèmes aux limites impliquant des EDO. Cependant, la question de
séparabilité d'une EDP en deux équations
différentielles ordinaires au plus n'est pas toujours possible. où X et Y sont des fonctions en x et y respectivement. Dans des
nombreux cas, l'EDP se réduit à deux équations
différentielles ordinaires pour X et Y. on obtient donc des
problèmes aux limites impliquant des EDO. Cependant, la question de
séparabilité d'une EDP en deux équations
différentielles ordinaires au plus n'est pas toujours possible.
II.2 EQUATION DE LA CHALEUR
Considérons le problème sur l'intervalle [O, L]
avec L  0 constitué de l'équation de la chaleur avec les
conditions aux limites de type Dirichlet et la condition initiale 0 constitué de l'équation de la chaleur avec les
conditions aux limites de type Dirichlet et la condition initiale
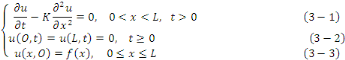
Où f est une fonction donnée et K une constante
positive.
Pour ce problème, nous cherchons à
déterminer des solutions 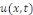 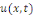 non triviales de la forme non triviales de la forme 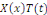 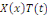 où où 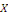 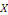 et et 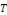 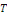 sont des fonctions de x et t respectivement ayant au moins des
dérivées premières et secondes continues. sont des fonctions de x et t respectivement ayant au moins des
dérivées premières et secondes continues.
ETAPE 1 : Remplaçons 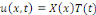 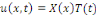 dans l'équation dans l'équation 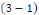 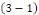 on obtient : on obtient :
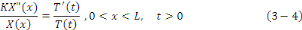
Puisque   et et   sont des variables indépendantes, cette relation implique qu'il
existe une constante sont des variables indépendantes, cette relation implique qu'il
existe une constante   appelée constante de séparabilité telle
que : appelée constante de séparabilité telle
que :
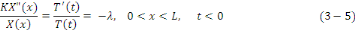
Comme nous cherchons des solutions ne s'annulant pas
identiquement, alors il existe
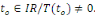
Conséquemment on obtient :
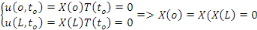
L'équation  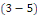 conduit au système d'EDOs suivant : conduit au système d'EDOs suivant :

Et

Où   est une constante (appelée valeur propres aux problèmes)
aux limites. est une constante (appelée valeur propres aux problèmes)
aux limites.
ETAPE 2 : Commençons d'abord à
résoudre le système 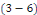 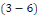 . Une solution non triviale de . Une solution non triviale de 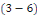 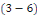 est appelée fonction propre avec la valeur propre est appelée fonction propre avec la valeur propre   (constante de séparation), en distingue 3 cas : (constante de séparation), en distingue 3 cas :
1er cas : si 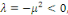 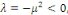 alors alors
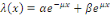 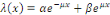
où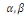 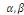 sont des constantes arbitraires. sont des constantes arbitraires.
Les conditions aux limites donnent :
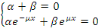
De la première équation, on a 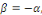 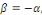 la seconde équation implique donc : la seconde équation implique donc :
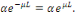 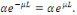 Alors si Alors si 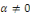 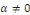 , nous obtenons , nous obtenons 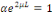 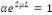 , ceci n'est pas possible car , ceci n'est pas possible car 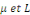 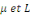 sont différent de 0 et par conséquent sont différent de 0 et par conséquent 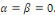 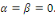
Alors dans ce cas 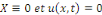 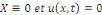 pour tout pour tout 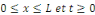 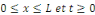 . .
Nous devons donc exclure le cas de 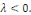 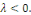
2ème CAS : si 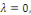 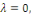 nous obtenons nous obtenons
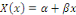
Où 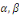 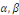 sont des constantes arbitraires. sont des constantes arbitraires.
Les conditions aux limites impliquent
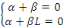
Comme 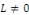 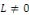 , il est claire que , il est claire que 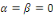 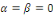 , alors dans ce cas , alors dans ce cas 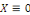 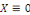 et et 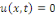 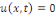 pour tout pour tout 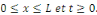 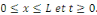 Nous devons donc exclure ce cas Nous devons donc exclure ce cas   =0. =0.
3ème CAS : 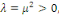 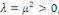 alors alors
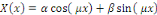
Où 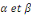 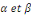 sont sont des constantes arbitraires. sont sont des constantes arbitraires.
Les conditions aux limites impliquent
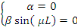
Pour éviter la solution triviale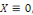 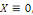 on suppose que on suppose que 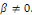 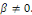 Ceci implique que Ceci implique que 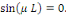 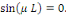 Conséquemment Conséquemment
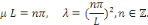
Il résulte que
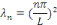
Sont des valeurs propres de 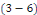 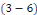 et les fonctions caractéristiques du problème et les fonctions caractéristiques du problème 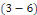 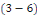 est : est :
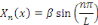
Comme 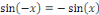 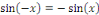 pour tous pour tous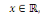 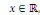 il suffit donc de considérer il suffit donc de considérer
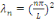 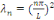 , , 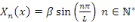 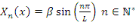
Il reste maintenant à résoudre le
problème 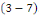 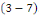 La solution de ce dernier est donnée par La solution de ce dernier est donnée par
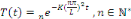
A la fin de cette étape, nous pouvons considérer
qu'on a bien construit une base hilbertienne.
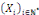
ETAPE 3 : Utilisons maintenant le principe superposition
générale pour générer à partir de 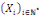 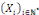 et et 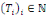 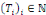 une solution plus générale du problème sous la
forme d'une série infinie de solutions séparées. Nous
avons ainsi obtenu la suite de solutions séparées : une solution plus générale du problème sous la
forme d'une série infinie de solutions séparées. Nous
avons ainsi obtenu la suite de solutions séparées :
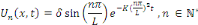
Par principe de superposition impliquant que toute combinaison
linéaire
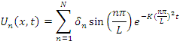
La fonction 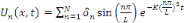 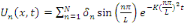 est solution de l'équation de la chaleur. est solution de l'équation de la chaleur.
Ceci conduit immédiatement à la question :
peut-on écrire une fonction quelconque 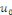 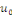 nulle pour nulle pour 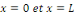 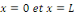 sous la forme d'une série sous la forme d'une série
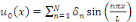 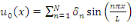 ? ?
La réponse est positive, comme on va le voir. Pour
étudier la possibilité de 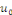 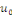 en série de en série de 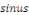 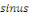 , on se ramène au cas bien connu des fonctions
périodiques. On suppose que , on se ramène au cas bien connu des fonctions
périodiques. On suppose que 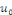 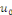 est continue sur est continue sur 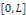 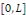 , avec , avec 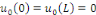 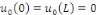 afin que les conditions aux limites soient vérifiées par
la donnée initiale. On commence par prolonger afin que les conditions aux limites soient vérifiées par
la donnée initiale. On commence par prolonger 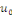 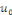 sur sur 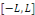 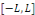 en posant en posant 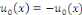 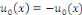 pour pour 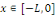 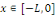 . Puisque . Puisque 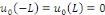 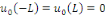 , on peut encore prolonger , on peut encore prolonger 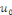 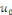 à tout R en fonction continue, impaire et à tout R en fonction continue, impaire et 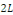 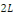 -périodique. De plus, si -périodique. De plus, si 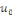 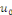 est de classe est de classe 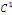 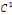 sur sur 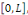 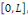 la fonction prolongée est la fonction prolongée est 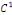 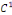 par morceaux sur tout R. Avec ces hypothèses sur par morceaux sur tout R. Avec ces hypothèses sur 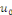 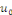 , le prolongement de , le prolongement de 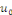 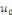 , que l'on notera encore , que l'on notera encore 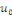 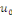 , se développe en séries de Fourier selon , se développe en séries de Fourier selon
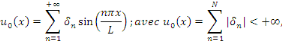
Ce qui assure la convergence en tout point 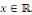 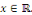 Les Les 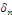 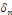 sont des coefficients de Fourier trigonométriques impaires de sont des coefficients de Fourier trigonométriques impaires de
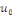 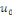 , le coefficient paire , le coefficient paire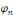 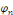 étant nul car étant nul car 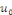 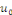 est impaire. est impaire.
Existence et unicité de la solution de
l'équation de la chaleur :
L'analysemenée dans la section précédente
permet d'obtenir un candidat solution de l'équation   , et donc d'énoncer la proposition suivante : , et donc d'énoncer la proposition suivante :
Proposition   : soit : soit 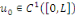 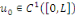 avec avec 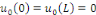 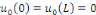 . On peut prolonger . On peut prolonger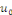 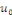 en fonction impaire et en fonction impaire et 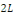 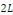 périodique, que l'on note encore périodique, que l'on note encore 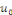 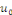 . .
Notons
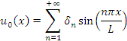
Son développement en série de Fourier, alors la
fonction
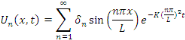
est solution du problème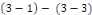 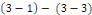 avec régularité avec régularité
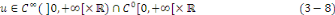
Démonstration : posons pour tout 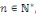 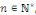
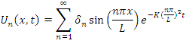
Les fonctions 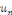 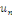 sont de classe sont de classe 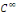 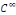 sur sur 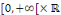 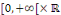 . comme . comme 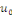 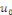 est continue et est continue et 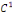 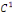 par morceaux, la série des coefficients de Fourier converge
absolument, par morceaux, la série des coefficients de Fourier converge
absolument,
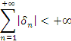
La majoration
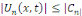
Valable pour tout 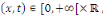 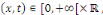 démontre alors la convergence normale de la série de
fonction démontre alors la convergence normale de la série de
fonction 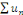 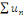 sur cet ensemble. Ainsi, sur cet ensemble. Ainsi,   est continue sur est continue sur 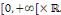 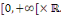
Soient 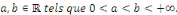 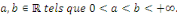 Pour tout Pour tout 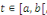 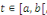 on a la majoration on a la majoration
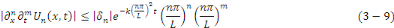
Avec 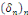 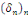 bornée car la série bornée car la série 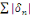 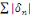 converge, donc, converge, donc, 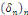 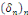 converge vers converge vers  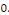 Nous avons donc la convergence uniforme de toutes les
dérivées Nous avons donc la convergence uniforme de toutes les
dérivées 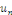 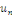 sur sur 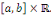 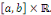 Ainsi Ainsi   est de classe est de classe 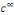 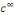 sur sur 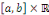 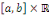 pour tout pour tout 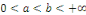 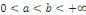 et donc sur et donc sur 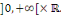 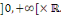 On peut alors dériver la série de terme à terme
sur cet ensemble, ce qui donne On peut alors dériver la série de terme à terme
sur cet ensemble, ce qui donne
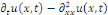
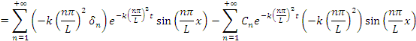
Pour tout  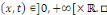
On peut maintenant se poser la question de l'unicité de
la solution. Pour commencer, on annonce un principe de maximum pour
l'équation de la chaleur.
Lemme 3.1 : soit 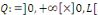 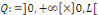 Soit Soit 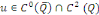 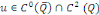 telle que telle que
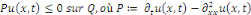
soient 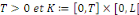 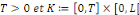 alors alors

Autrement dit   atteint son maximum pour atteint son maximum pour 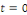 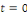 ou ou 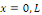 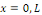 et et 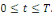 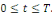
Démonstration : soit 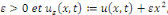 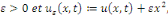 qui vérifie donc qui vérifie donc 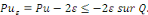 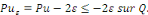 Soit Soit 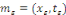 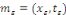 un point de un point de 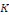 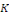 où où 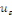 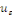 atteint son maximum sur atteint son maximum sur 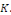 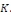 Supposons par absurde que Supposons par absurde que 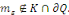 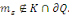 Alors : Alors :
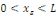 · · 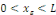 donc, donc, 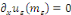 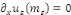 et et 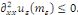 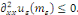
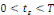 · · 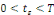 donc, donc,
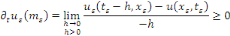
Ainsi , 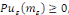 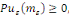 ce qui contredit ce qui contredit 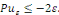 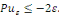 Donc, Donc, 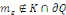 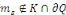 et et
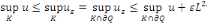
En prenant la limite quand 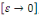 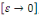 on obtient on obtient 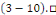 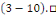
Théorème 3. 1 (d'unicité) le
problème 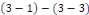 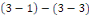 admet une solution unique admet une solution unique 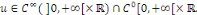 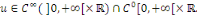
Démonstration : soit 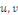 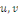 deux solutions de deux solutions de 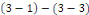 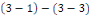 . Posons . Posons 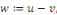 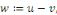 alors alors 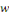 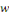 est aussi solution de est aussi solution de 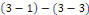 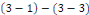 et et
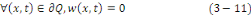
Fixons 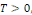 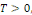 puisque puisque 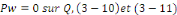 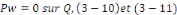 entraînent entraînent 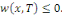 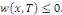 En faisant de même avec En faisant de même avec 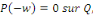 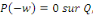 on obtient on obtient 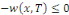 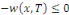 , d'où , d'où 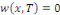 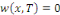 , pour tout , pour tout 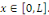 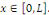 Puis que T est arbitraire, on a bien Puis que T est arbitraire, on a bien 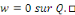 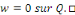
comment calculer les coefficients 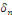 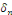 . .
Remarquons :
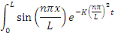
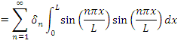
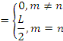
Par conséquent, les coefficients de Fourier sont
donnés par :
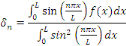
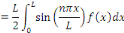
Puisque 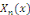 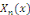 est orthogonale, nous obtenons la formule explicite de la solution
formelle, qui est donnée par : est orthogonale, nous obtenons la formule explicite de la solution
formelle, qui est donnée par :
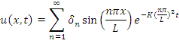
Où
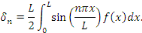
| 


