II.5 CAS D'UNE PERIODE QUELCONQUE. [8]
En physique, on rencontre des fonctions admettant une
période 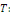 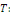 pour tout nombre réel pour tout nombre réel  
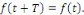
La variable   représente souvent le temps. représente souvent le temps.
On se ramène au cas de la période 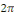 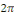 grâce au changement de variable grâce au changement de variable
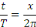
Le nombre 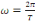 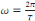 s'appelle fréquence fondamentale ou pulsation angulaire de
récurrence. Les multiples s'appelle fréquence fondamentale ou pulsation angulaire de
récurrence. Les multiples 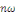 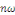 de la fréquence fondamentale, où de la fréquence fondamentale, où 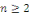 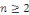 sont appelés Harmoniques. sont appelés Harmoniques.
La série de Fourier d'une fonction   admettant admettant 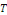 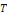 pour période est définie par la formule : pour période est définie par la formule :
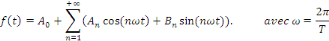
Les coefficients de Fourier sont donnés par les
formules :

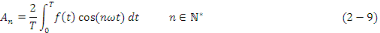
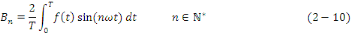
II.6 CALCUL PRATIQUE DES COEFFICIENTS DE FOURIER [8]
Le calcul des coefficient de Fourier d'une fonction
périodique   est généralement long et fastidieux. est généralement long et fastidieux.
Corolaire 2. 1 [8] soit   une fonction définie sur R, 2 une fonction définie sur R, 2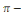 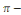 périodique et intégrable sur périodique et intégrable sur 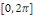 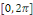 . .
- Si   est paire, alors pour tout est paire, alors pour tout 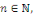 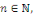 on a on a 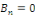 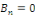 et et
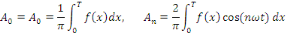
- Si   est impaire, alors pour tout est impaire, alors pour tout 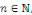 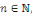 on a on a 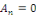 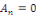 et et
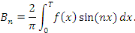
Démonstration : supposons que   est paire, est paire, 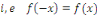 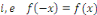 et considérons et considérons 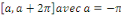 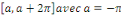 . En utilisant la relation de chasles, on obtient pour tout . En utilisant la relation de chasles, on obtient pour tout 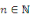 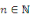 : :
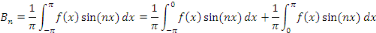
La fonction   étant impaire, le changement de variable étant impaire, le changement de variable 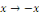 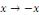 implique que implique que
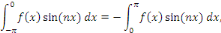
Ce qui implique que 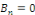 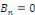
On obtient aussi en utilisant le changement de variable 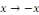 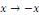 , compte tenu de la parité de , compte tenu de la parité de 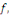 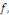 que pour tout que pour tout 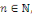 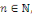
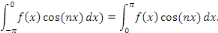
Cela implique que pour tout 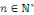 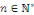
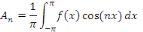
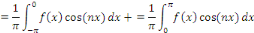
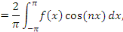
Et que
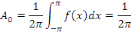
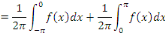
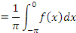
Dans le cas où   est impaire, les relation données s'obtiennent de façon
similaire. ? est impaire, les relation données s'obtiennent de façon
similaire. ?
II.7 FORME COMPLEXE D'UNE SERIE DE FOURIER [8]
La série de Fourier d'une fonction   satisfaisant aux conditions du théorème satisfaisant aux conditions du théorème 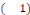 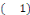 de Léjeune-Dirichlet peut se mettre sous la forme complexe en
tout point x où elle converge. Dans ces conditions, nous pouvons
écrire : de Léjeune-Dirichlet peut se mettre sous la forme complexe en
tout point x où elle converge. Dans ces conditions, nous pouvons
écrire :
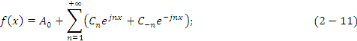
Où
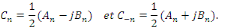
Nous allons montrer que les coefficients 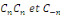 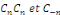 s'expriment simplement en fonction de s'expriment simplement en fonction de   sous la forme d'intégrales, voire plus simplement que les
coefficients sous la forme d'intégrales, voire plus simplement que les
coefficients 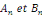 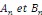 . .
Appliquons en effet les formules d'Euler :
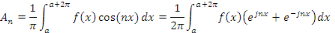
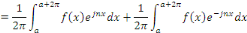
De même
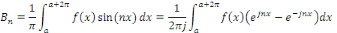
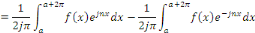
Il en découle aussitôt que
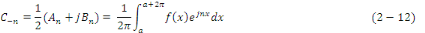
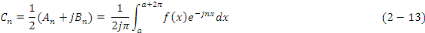
On remarque que 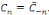 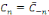 Les coefficients de Fourier sous forme complexe sont donc deux à
deux conjugués. De plus, on passe de la formule Les coefficients de Fourier sous forme complexe sont donc deux à
deux conjugués. De plus, on passe de la formule 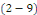 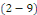 à la formule à la formule 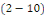 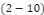 en changeant en changeant   et et 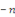 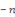 . Enfin, lorsqu'on remplace . Enfin, lorsqu'on remplace   par par   dans l'une ou l'autre de ces formules, on trouve : dans l'une ou l'autre de ces formules, on trouve :

Ainsi, la formule 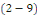 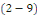 est valable non seulement pour tout entier naturel non nul est valable non seulement pour tout entier naturel non nul   , mais aussi , mais aussi 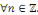 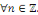
En résumé,

Où, pour tout entier rationnel 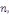 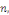
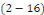 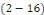
Le cas d'une fonction de période 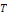 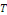 se ramène au précédent, grâce encore au
changement de variable. se ramène au précédent, grâce encore au
changement de variable.
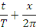
Ainsi,

Où, pour tout 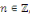 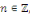

Dans le cas où il est nécessaire de retrouver le
coefficient réel 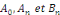 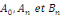 à partir des coefficients à partir des coefficients 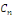 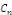 , il suffit de remarquer que , il suffit de remarquer que
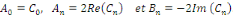 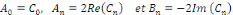 [8] [8]
| 


