II.3. SERIES DE FOURIER
Définition 2. 2 [8] soit   une fonction définie sur R à valeurs réelles,
intégrable sur tout intervalle de longueur une fonction définie sur R à valeurs réelles,
intégrable sur tout intervalle de longueur 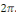 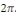
Nous nous proposons d'étudier l'existence et
l'unicité d'une s&rie trigonométrique convergent en tout
point x deR et telle que
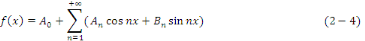
Supposons d'abord qu'il existe une telle série
trigonométrique. Nous allons montrer que l'on peut démontrer les
coefficients 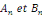 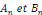 d'une manière et d'une seule. d'une manière et d'une seule. 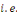 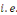 L'unicité de la série trigonométrique
cherchée. L'unicité de la série trigonométrique
cherchée.
Cette méthode nous fournira en même temps des
formules constamment utilisées en pratique pour le calcul effectif des
coefficients.
Calcul de 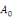 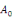 : Intégrons les deux membres de la relation : Intégrons les deux membres de la relation 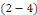 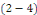 entre entre 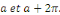 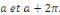
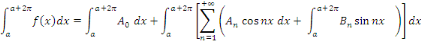
Admettons que l'on puisse intervertir les symboles  
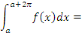
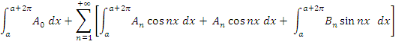
Puisque, pour tout entier naturel non nul n,
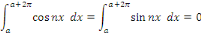
D'où,
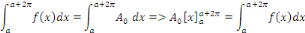
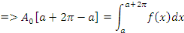

Cette intégrale n'est autre que la valeur moyenne de
  sur l'intervalle considéré. sur l'intervalle considéré.
Calcul de 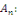 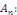 Multiplions les deux membres de Multiplions les deux membres de 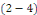 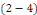 par par 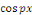 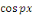 et intégrons entre et intégrons entre   et et 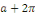 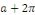
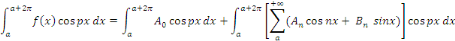
Intégrons les symboles  
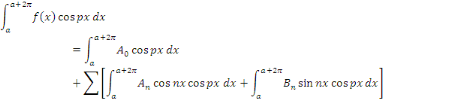
Par orthogonalité des fonctions 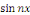 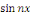 et et 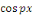 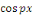 pour tout pour tout
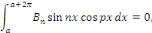
Ainsi que celle des fonctions 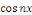 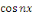 et et 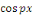 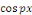 pour tout entier pour tout entier   autre que autre que   , ,
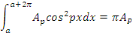
D'où,
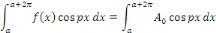
Car
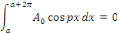
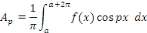
Aux notations près, pour tout naturel non nul n,
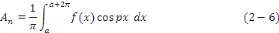
Calcul de 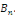 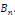 [8] Multiplions les deux membres de [8] Multiplions les deux membres de 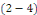 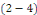 par par 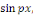 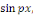 puis intégrons entre puis intégrons entre 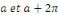 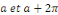 . .
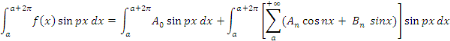
Admettons que l'on intervertisse les symboles 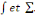 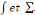
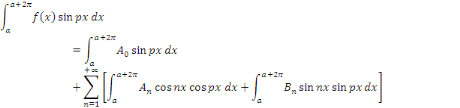
Par orthogonalité des fonctions 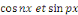 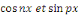 pour tout entier pour tout entier   autre que autre que  
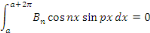
Ainsi que celle des fonctions 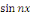 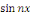 et et 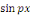 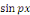 pour tout entier pour tout entier   autre que autre que   , ,
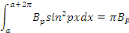
D'où,
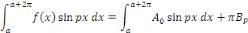
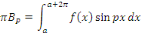
Car
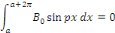
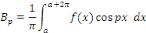
Aux notations près, pour tout naturel non nul n,
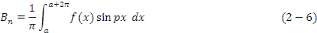
Exemple 2. 2 [1] considérons une fonction 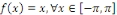 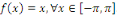 Trouver sa série de Fourier. Trouver sa série de Fourier.
Solution : calculons d'abord les coefficients de
Fourier.
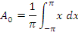
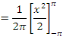
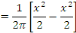
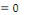
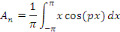
En intégrant par parties, posons :
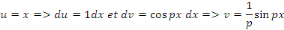
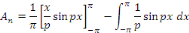
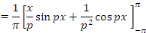
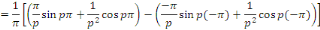
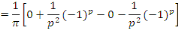
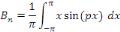
Posons toujours en intégrant par parties
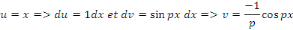
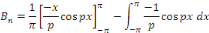
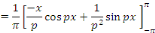
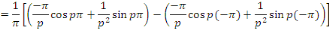
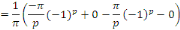
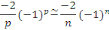
Donc, la série de Fourier de la fonction donnée
est :
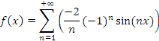
Si   est paire, est paire, 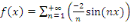 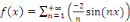
Si   est impaire, est impaire, 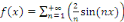 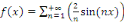
II.4 CONVERGENCE ET SOMME DES SERIES DE FOURIER
Théorème 2. 1[8] (de
Lejeune-Dirichlet) : soit une fonction numérique définie
sur R, admettant 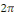 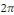 pour période, continûment dérivable sur le
complémentaire d'une partie finie pour période, continûment dérivable sur le
complémentaire d'une partie finie 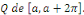 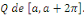 On suppose que On suppose que 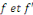 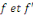 admettent des limites à gauche et des limites à
droite en tout point de admettent des limites à gauche et des limites à
droite en tout point de   . Alors la série de Fourier de . Alors la série de Fourier de   converge en tout point converge en tout point 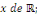 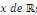 sa somme est égale à sa somme est égale à
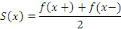
C'est-à-dire à la somme des limites à
gauche et à droite de   au point au point 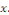 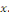
En particulier, en tout point 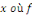 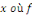 est continue, est continue, 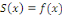 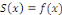
En plus, si   est continue sur est continue sur 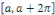 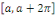 , la série de Fourier de , la série de Fourier de  converge absolument et uniformément vers converge absolument et uniformément vers   . .
Démonstration : dans [8], le
théorème 2.1 assurant l'existence d'un développement en
série de Fourier est énoncé sans démonstration.
Nous nous aspirons de [1] alors pour le démontrer.
Pour tout réel 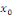 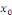 , notons , notons 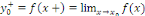 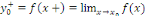 la limite de la limite de   à gauche en à gauche en  
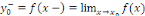 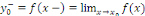 la limite de la limite de   à droite en à droite en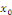 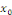 et et
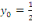 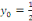 ( (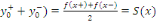 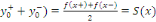
Notons que 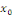 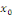 est un point où est un point où   est continue, alors est continue, alors 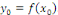 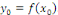 Pour montrer que le théorème 2.1, nous allons montrer que
la suite Pour montrer que le théorème 2.1, nous allons montrer que
la suite 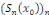 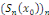 des sommes partielles associée à la série de
Fourier de des sommes partielles associée à la série de
Fourier de   converge et a pour limite converge et a pour limite 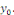 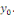
D'après la formule de Dirichlet, la somme partielle
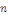  en en 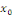 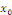 est donnée par est donnée par
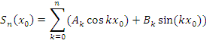
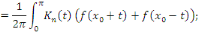
Où 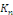 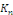 est une fonction est une fonction 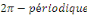 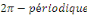 définie sur définie sur 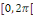 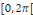 par par
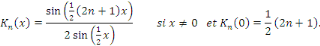
Puisque
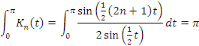
Et que 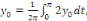 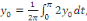
On a 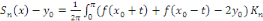 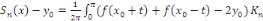 (t) dt. (t) dt.
Considérons la fonction   de de  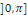 dans R définie par dans R définie par
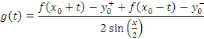
Comme par hypothèse   est dérivable par morceaux, les deux limites suivantes
existent : est dérivable par morceaux, les deux limites suivantes
existent :
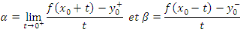
De plus comme 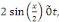 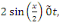 on a : on a :
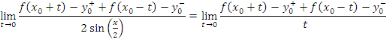
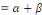
Ainsi, la fonction   est prolongeable par continuité en 0 en posant est prolongeable par continuité en 0 en posant 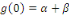 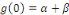 . Comme . Comme   est est   et dérivable par morceaux sur et dérivable par morceaux sur   0, 0,  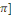 et par conséquent intégrable sur et par conséquent intégrable sur   0, 0, 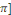 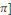 . On déduit que : . On déduit que :
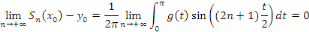
Ainsi donc, la suite 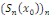 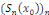 converge et a pour limite converge et a pour limite 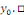 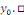
| 


