Proposition 2.1[1] Si les séries
numériques  convergent absolument, alors la série trigonométrique dont
le terme général convergent absolument, alors la série trigonométrique dont
le terme général   converge normalement (et par conséquent simplement, absolument et
uniformément) sur R. converge normalement (et par conséquent simplement, absolument et
uniformément) sur R.
Démonstration : les fonctions sinus et
cosinus étant majorées par 1 et minorées par -1, pour tout
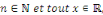 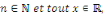 on a : on a :
|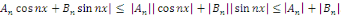 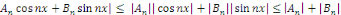
On en déduit que 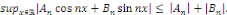 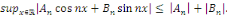
Si les séries numériques 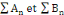 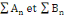 convergent absolument alors la série de terme
général convergent absolument alors la série de terme
général 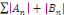 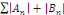 converge. D'après les critères de convergence pour les
séries à termes positifs (soient converge. D'après les critères de convergence pour les
séries à termes positifs (soient 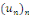 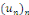 et et 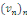 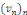 deux suites réelles à positifs telles que : deux suites réelles à positifs telles que :
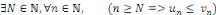
· Si la série 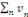 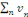 converge, alors la série converge, alors la série 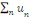 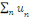 converge. converge.
· Si la série 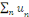 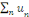 diverge, alors la série diverge, alors la série 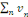 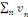 diverge), la série de terme général diverge), la série de terme général 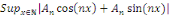 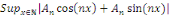 converge. Par définition, cela signifie que la série converge. Par définition, cela signifie que la série 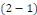 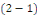 converge normalement sur R.??? converge normalement sur R.???
II. 1. 1. PROPRIETE DE LA SOMME D'UNE SERIE TRIGONOMETRIQUE
[1]
On dit qu'une fonction définie sur un sous-ensemble ??D
de R est 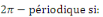 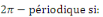
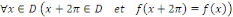
La période d'une telle fonction peut être
inférieure à 2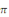 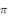 ; c'est le cas par exemple de l'application ; c'est le cas par exemple de l'application 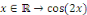 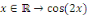 qui est qui est 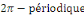 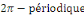 et qui admet pour période fondamentale et qui admet pour période fondamentale 
Proposition 2.2La somme d'une série
trigonométrique est une fonction 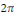 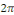 -périodique. -périodique.
Démonstration : soit 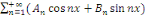 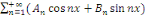 est un série trigonométrique qui converge en est un série trigonométrique qui converge en 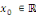 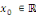 . Pour tout . Pour tout 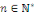 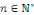 , on a : , on a :
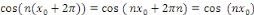
Et
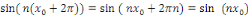
Ces relations sont encore valables si 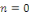 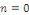 . On en déduit que les deux séries . On en déduit que les deux séries
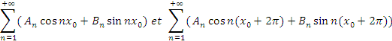
Sont égales. Elles ont donc la même somme. ???
II. 1. 2. FORME COMPLEXE D''NE SERIE TRIGONOMETRIQUE
[8]
En appliquant les formules d'Euler, nous obtenons une nouvelle
forme, dite complexe. Ecrivons en effet,
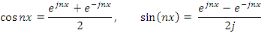
Alors,
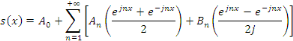
Ordonnons les termes entre crochets :
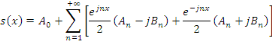
Posons 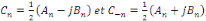 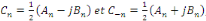
Nous remarquons déjà que ces deux coefficients
sont des nombres complexes conjugués :  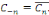
La série peut donc s'écrire sous la forme
complexe :
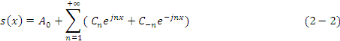
Ainsi, nous pouvons considérer une série
trigonométrique comme une série des fonctions de la forme 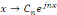 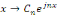 , où , où 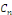 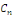 est un nombre complexe, mais où, cette fois, l'ensemble des
indices est Z, et non plus N. est un nombre complexe, mais où, cette fois, l'ensemble des
indices est Z, et non plus N.
II.2 FONCTIONS ORTHOGONALES [8]
Considérons l'espace vectoriel 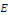 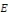 sur R des fonctions continues sur un même intervalle [a, b] de R
à valeurs réelles, où sur R des fonctions continues sur un même intervalle [a, b] de R
à valeurs réelles, où 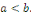 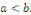
L'application

Est une fonction bilinéaire symétrique
satisfaisant aux deux conditions suivantes :
a. Pour tout élément 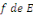 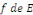 , le nombre réel , le nombre réel 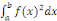 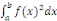 est positif ; est positif ;
b. Le nombre réel 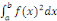 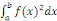 est nul si et seulement si la fonction est nul si et seulement si la fonction   est nulle. est nulle.
Ainsi, on dit que des fonctions 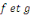 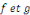 sont orthogonales si leur produit scalaire est nul,
c'est-à-dire si sont orthogonales si leur produit scalaire est nul,
c'est-à-dire si
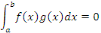
Exemple 2. 1 Soient [-1, 1] et les fonctions 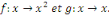 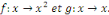
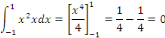
| 


