Une copule est une fonction de répartition
multivariée C définie sur l'hypercube
0;11n et dont les marginales sont uniformes
sur 0;1 . Le théorème de SKlar (1959) dit
que « si F est une fonction de
répartition n-dimensionnelle avec des
marginales
F1,...,Fn , alors il existe une
n-copule C telle que pour tout x de Rn
,
F(x1,...,;)=
C[F(x1),...,Fn(xn)1
». Ainsi, si ( X1, ...Xn )
est un vecteur de variables
aléatoires continues admettant
F1,...,Fn comme fonctions de
répartition marginales et F
comme fonction de répartition jointe, alors il existe
une copule C qui vérifie la
relation
précédente. Si les marginales
F1,...,Fn sont continues, alors C
est unique, autrement C
est uniquement déterminée sur
Im(F1)*...* Im(Fn ) , avec
Im(X) représentant l'ensemble des valeurs prises par
X.
On s'aperçoit donc qu'une copule permet d'exprimer une
fonction de répartition multivariée selon ses marginales et que
cette copule résume toute la structure de dépendance. De fait,
les copules présentent de nombreux avantages pour modéliser la
dépendance entre risques. D'une part, elles permettent de décrire
le comportement individuel de chaque risque et « couplent » les lois
marginales pour obtenir la loi jointe. D'autres part, elles offrent une
représentation fonctionnelle de la dépendance qui donne une
description très complète de la forme de cette
dernière.
Il est important de rappeler que la dépendance et la
corrélation sont des notions
différentes. En effet, on a
X et Y indépendantes X et Y non
corrélées ou
(X, Y) = 0 9mais la
réciproque est fausse sauf dans le cas où les variables sont
gaussiennes car la dépendance est alors entièrement
caractérisée par le coefficient de corrélation. Bien qu'il
soit facile à calculer et fréquemment présent dans les
travaux actuariels, en assurance comme en finance, le coefficient de
corrélation doit être
n
(Xt -- X)(Yt --Y)
9 P(X ,Y)=
t=1 où X et Y sont les variables
(actifs à comparer)
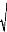
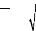
n n
(Xt-X)2* E(Yt-Y)2
t1 t1
utilisée avec précaution car il n'est pertinent
qu'en présence de distributions elliptiques (distribution
multivariée Normale ou de Student) ou de dépendance
linéaire. Les erreurs d'interprétation et limites liées
à son utilisation sont discutées dans Embrechts et al.
[1999] et surtout sur le marché du crédit.
Bien que les copules puissent fournir une approche assez
intéressante au marché de crédit, la première
décision à prendre est relative à la sélection de
la copule qui sied le mieux à nos données. Cela est dû au
fait qu'il en existe différents types, avec des caractéristiques
différentes (copules archimédiennes : gaussienne et de Student
dites copules elliptiques qui ont l'avantage de décrire des structures
de dépendance très diverses dont celles dites
asymétriques, où les coefficients de queue inférieure et
supérieure diffèrent, copules HRT, copules empiriques). En outre,
chaque copule aura des paramètres qui modifient la relation entre les
variables. Ces paramètres peuvent être difficiles à
calibrer lorsqu'il y a très peu de données ou d'informations de
marché fiables comme c'est le cas du marché des CDO.
Ces dernières années, le marché standard
des « CreditMetrics », pour l'évaluation et la
modélisation de la corrélation des portefeuilles de
crédits des tranches de CDO (DJ Tranched TRAC-X), a été
décrit comme la copule gaussienne. En effet, une copule gaussienne
définie la relation de dépendance entre les rendements des actifs
dans un portefeuille de crédit comme multivariée normale. En
outre, cette relation jointe, normalement distribuée, est
indépendante de la distribution réelle des rendements des actifs
pris individuellement. Il a été grossièrement
supposé, dans les modélisations, que les distributions des
rendements marginales sont normales. Pourtant, en pratique, il est possible
d'avoir des variables aléatoires avec des distributions marginales non
normales (Student-t par exemple) et puis utiliser une copule gaussienne pour
définir la relation entre ces deux variables1°.
Dans le but de mieux appréhender cette notion de
distribution jointe, le moyen le plus simple est de considérer deux
variables (actifs). Ensuite, il faut construire le diagramme de dispersion des
deux variables et observer la forme du nuage de points
1° JPMorgan -- Credit Derivatives Strategy --
March 2°°4
résultant. En général, si le nuage de
points a une forme elliptique comme la figure 4, alors les variables ont une
distribution jointe normale et il est donc possible d'utiliser la
corrélation comme une mesure de dépendance entre les deux
variables. Lorsque la corrélation entre les deux variables augmente, les
points vont converger et devenir comme une ligne (cf. figure 6). Cependant,
lorsque la forme est significativement différente d'une ellipse,
précisément avec une concentration des points dans un endroit,
alors, il n'est pas prudent d'utiliser un simple nombre de
corrélation.
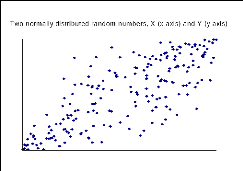
Figure 5 : Joint normal scatter, corrélation=80%
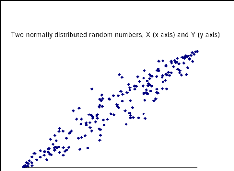
Figure 6: Joint normal scatter,
corrélation=95%
Source: JPMorgan.
Considérons maintenant une distribution jointe qui
n'est pas normale telle des probabilités de défaut de
crédit jointes. La figure 7 montre la même distribution normale
jointe que précédemment, avec une corrélation de 80%. La
figure 8, a aussi une corrélation de 80% mais une distribution qui est
plus typique au crédit. A première vue, il est clair que la
relation entre les deux variables est différente. En observant
l'extrémité supérieure droite de la figure 8, on remarque
qu'il y a une forte concentration de points pour les valeurs les plus
élevées. Cependant, il y a une plus grande dispersion des points
sur cette figure que sur la figure 7. Le type de relation illustré au
niveau de la figure 8 correspond à une évidence que les
corrélations de défaut entre les actifs est faible dans un
environnement de marché normal. Cependant, lorsque la probabilité
de défaut augmente pour un actif, alors, ce fait augmente celle des
autres comme dans le cas des récessions.
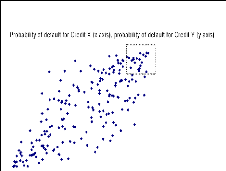
Figure 7: Joint normal scatter,
correlation=80%
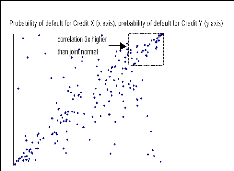
Figure 8 : Joint normal scatter, correlation=80%
Source: JPMorgan.
Ainsi, pour toute analyse d'indépendance sur le
marché du crédit, il importe de savoir exactement, de prime
abord, les variables sous-jacentes qui sont analysées. Ensuite, le
comportement de la relation doit être comprise avant d'utiliser la
corrélation linéaire comme mesure de dépendance. En effet,
il existe une confusion entre la corrélation des défauts et la
corrélation des rendements d'actifs. Cette confusion augmente parce
qu'alors qu'un facteur important dans l'évaluation des tranches de
crédit est la corrélation des défauts, le facteur requis
pour les modèles tels que « CreditMetrics » est la
corrélation des rendements d'actifs. La corrélation des
rendements peut donc être convertie en corrélation de
défaut au sein des modèles. La corrélation de
défaut est plus utilisée au niveau des crédits (tranches
de CDO par exemple) en raison de son impact direct sur l'évaluation des
produits dérivés complexes.
Cette analyse de la mesure du marché nous amène
à nous pencher sur le lieu d'émission et de placement d'un CDO.
Ce qui fait référence aux différents segments du
marché.



