4.2.2 Formulation du
modèle
Si l'on pose 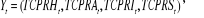 , le
vecteur des quatre variables représentant l'évolution de
l'activité économique au Cameroun. Avec les quatre séries
de variables intégrées à l'ordre 1, le modèle
théorique, composé de quatre équations
s'écrit de façon synthétique : , le
vecteur des quatre variables représentant l'évolution de
l'activité économique au Cameroun. Avec les quatre séries
de variables intégrées à l'ordre 1, le modèle
théorique, composé de quatre équations
s'écrit de façon synthétique :
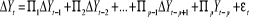
= 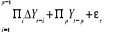
Avec 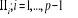 , matrices
(4,4) de paramètres , matrices
(4,4) de paramètres
 est un
entier naturel appelé ordre du modèle. est un
entier naturel appelé ordre du modèle.
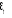 , un
vecteur (4,1) de termes d'erreur de type , un
vecteur (4,1) de termes d'erreur de type 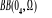 où
? est une matrice diagonale de dimension (4,4) définie positive, et où
? est une matrice diagonale de dimension (4,4) définie positive, et 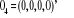
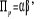 où où
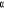 est la
force de rappel vers l'équilibre est la
force de rappel vers l'équilibre
et 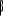 la matrice
dont les vecteurs sont les coefficients de la relation de long terme entre les
variables. la matrice
dont les vecteurs sont les coefficients de la relation de long terme entre les
variables.
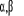 :
matrices (4,r) ; r étant le rang de :
matrices (4,r) ; r étant le rang de 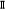 ou encore
le nombre de relations de long terme. ou encore
le nombre de relations de long terme.
Le modèle formulé ci-dessus est un modèle
VAR sous la forme d'un VECM. En réalité sa spécification
est consécutive à la significativité des tests de
co-intégration sur les séries de variables. L'encadré
ci-dessous présente les principes du test de la trace qui est un des
tests de co-intégration proposés par Johansen (1991) et Johansen
et Juselius (1990). Ces tests restent efficaces lorsque l'échantillon
n'est pas de très grande taille.
Encadré 3 :
Principes des tests de co-intégration
Si l'on considère un vecteur 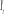 de N
variables I(1). La représentation VAR (p) de de N
variables I(1). La représentation VAR (p) de 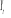 est
donnée par : est
donnée par :
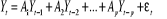
Cette relation peut se réécrire :
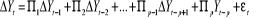
Dans cette relation tous les membres sont I(0) à
l'exception de 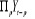 qui est I
(1). Il y a un déséquilibre entre le membre de gauche et celui de
droite. Il faut donc que qui est I
(1). Il y a un déséquilibre entre le membre de gauche et celui de
droite. Il faut donc que 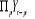 soit I
(0). soit I
(0).
On pose 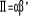
Où : 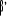 est une
matrice (r,N) contenant les r vecteurs de co-intégration est une
matrice (r,N) contenant les r vecteurs de co-intégration
et 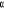 est une
matrice (N,r) contenant les poids associés à chaque vecteur de
co-intégration. est une
matrice (N,r) contenant les poids associés à chaque vecteur de
co-intégration.
En cas d'existence de r relations de co-intégrations,
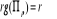 . Les
tests proposés par Johansen reposent sur cette condition. . Les
tests proposés par Johansen reposent sur cette condition.
Test de la trace
C'est un test basé sur les valeurs propres d'une
matrice calculée en deux étapes :
Etape 1 : calcul des résidus 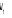 et et 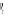
On estime les deux équations suivantes :
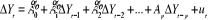
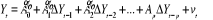
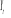 est un
vecteur de N variables I(1) est un
vecteur de N variables I(1)
Étape 2 : calcul de la matrice
permettant le calcul des valeurs propres
Quatre matrices de variance-covariance des résidus sont
calculées :
 ; ;
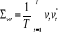 ; ; 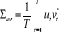 ; ;
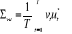
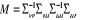 Les k
valeurs propres de M sont calculées. Les k
valeurs propres de M sont calculées.
La statistique du test de la trace est donnée par
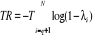
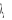 est la
ième valeur propre de M est la
ième valeur propre de M
q : rang de la matrice
TR suit une loi dont les valeurs ont été
tabulées par Johansen et Juselius (1990) puis par Osterwald-Lenum
(1992).
Trois cas peuvent se présenter :
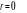 ·
: pas de relation de co-intégration. ·
: pas de relation de co-intégration. 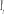 est I (1),
le VAR est estimé sur est I (1),
le VAR est estimé sur 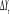
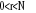 · , il
existe r relations de co-intégration ; la spécification
correcte du VAR est un ECM. · , il
existe r relations de co-intégration ; la spécification
correcte du VAR est un ECM.
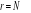 ·
: ·
: 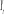 est stationnaire. Le VAR est estimé à niveau. est stationnaire. Le VAR est estimé à niveau.
Les valeurs critiques de ces statistiques de test
dépendent de la présence d'une constante dans la relation de
co-intégration ou l'ECM, et de la présence d'un trend dans la
relation de co-intégration.
| 


