I.2. Valeurs moyennes et fluctuations
I.2.1 Valeur moyenne
Un grand système peut être subdivisé en
sous-systèmes qui forment de nouveaux systèmes mécaniques
mais qui ne sont pas isolés, le grand système
considéré est isolé. La physique statistique se rapporte
à un système se trouvant en équilibre.
D'habitude est isolé cette condition d'équilibre
est vérifiée ; au contraire, les sous-systèmes sont
soumis à des actions diverses de la part des autres parties des
systèmes. A cause du grand nombre de degrés de liberté de
ces autres parties, les interactions ont un caractère compliqués
et enchevêtrés.
Ceci rend impossible les méthodes de la
mécanique. Par conséquent, la méthode statistique repose
essentiellement sur une certaine distribution statistique permettant de
calculer la valeur d'une grandeur quelconque.
En statistique classique, la valeur moyenne d'une grandeur
quelconque f(p,q) est donnée par la
formule :
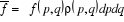 (1.1)
(1.1)
Où 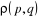 est la fonction de distribution statistique qui est égale
à la probabilité pour les coordonnées
qi et les impulsions
pi de prendre les valeurs se
trouvant dans les intervalles infiniment petits qi,
pi et qi+dqi,
pi+dpi est la fonction de distribution statistique qui est égale
à la probabilité pour les coordonnées
qi et les impulsions
pi de prendre les valeurs se
trouvant dans les intervalles infiniment petits qi,
pi et qi+dqi,
pi+dpi
(avec i =1,2,...,N)
q = (q1,q2,...,qN)
est l'ensemble des coordonnées généralisées,
p = (p1,p2,...,pN)
est l'ensemble des impulsions généralisées
dq = dq1dq2...dqN ;
dp = dp1dp2...dpN,
N est le nombre de degrés de liberté
La moyenne trouvée 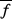 à l'aide de la fonction de distribution est appelée
statistique. La statistique permet de faire les
prédictions se réalisant avec une grande précision pour la
majeure partie d'un intervalle de temps suffisamment long pour que l'influence
des conditions initiales disparaisse. En ce sens, les prédictions de la
statistique ont un caractère non pas aléatoire mais pratiquement
déterminé. On dit qu'un système se trouve en
équilibre statistique, de même qu'en équilibre
thermodynamique ou thermique, si les grandeurs physiques macroscopiques
caractérisant chacune de ses parties sont égales, avec une
précision relativement grande à leurs moyennes. à l'aide de la fonction de distribution est appelée
statistique. La statistique permet de faire les
prédictions se réalisant avec une grande précision pour la
majeure partie d'un intervalle de temps suffisamment long pour que l'influence
des conditions initiales disparaisse. En ce sens, les prédictions de la
statistique ont un caractère non pas aléatoire mais pratiquement
déterminé. On dit qu'un système se trouve en
équilibre statistique, de même qu'en équilibre
thermodynamique ou thermique, si les grandeurs physiques macroscopiques
caractérisant chacune de ses parties sont égales, avec une
précision relativement grande à leurs moyennes.
En mécanique quantique, la valeur moyenne de toute
grandeur caractérisant le système, ainsi que les
probabilités des différentes valeurs de ces grandeurs sont
déterminées à l'aide de la matrice densité.
Ainsi, la valeur moyenne de toute grandeur f à
l'état donné est :
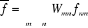 ` (1.2) ` (1.2)
Où 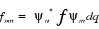 sont les éléments matriciels de la grandeur f sont les éléments matriciels de la grandeur f
 est l'opérateur correspondant et est l'opérateur correspondant et 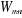 dépendant généralement du temps, est l'ensemble des
grandeurs qui représentent la matrice densité. [5] dépendant généralement du temps, est l'ensemble des
grandeurs qui représentent la matrice densité. [5]
Les distributions statistiques des sous-systèmes
doivent, par définition de l'équilibre statistique, être
stationnaires. Par conséquent, les matrices statistiques 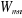 de tous sous-systèmes sont diagonales ; la
grandeur de tous sous-systèmes sont diagonales ; la
grandeur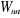 , notée aussi par , notée aussi par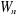 , est la distribution de probabilité. , est la distribution de probabilité.
Par suite, la formule déterminant la valeur moyenne
d'une grandeur f se trouve ainsi simplifiée.
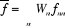 (1.3) (1.3)
Avec 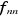 les éléments matriciels diagonaux. les éléments matriciels diagonaux.
| 


