I.3. Gaz parfait
Un gaz parfait est un gaz dont la pression est si basse que
ses atomes ou ses molécules se déplacent indépendamment
l'un de l'autre. En d'autres termes, un gaz parfait peut être
considéré comme un ensemble des boules (molécules) en
mouvement chaotique. Les molécules doivent avoir un volume propre
négligeable et n'interagissent pas l'une de l'autre à distance.
Ces molécules entrent continuellement en collision avec d'autres
molécules du gaz parfait et avec des parois du récipient en
exerçant sur elles une certaine pression [3] et [8].
Pour un gaz parfait classique, les particules identiques le
constituant peuvent être distinguées (sont discernables) tandis
que pour un gaz parfait quantique, les particules identiques le constituant ne
peuvent pas être distinguées (sont indiscernables).
I.4. Distribution grand canonique de Gibbs
Dans la pratique, nous avons affaire aux systèmes
macroscopiques, c'est-à-dire constitués par un grand nombre de
particules (atomes, molécules, etc.). D'où l'importance de
l'application des méthodes statistiques pour l'étude de tels
systèmes. Nous pouvons définir la distribution grand canonique
pour un système macroscopique.
La distribution grand canonique quoi que conceptuellement plus
élaborée, simplifie les calculs physiques sur les systèmes
quantiques. [4] et [5]
La distribution grand canonique de Gibbs
s'écrit :
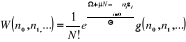 (1.6) (1.6)
Où 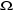 est le potentiel généralisé ou le grand
potentiel, est le potentiel généralisé ou le grand
potentiel,
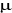 est le potentiel chimique, est le potentiel chimique,
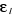 est le niveau énergétique, est le niveau énergétique,
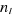 est le nombre de particules occupant le niveau énergétique est le nombre de particules occupant le niveau énergétique
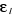 , ,
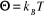 avec avec 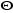 est le module de la distribution canonique, est le module de la distribution canonique,
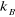 est la constante de Boltzmann, est la constante de Boltzmann,
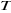 est la température du système, est la température du système,
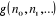 est une grandeur exprimant le degré de
dégénérescence des niveaux énergétiques est une grandeur exprimant le degré de
dégénérescence des niveaux énergétiques
Sachant que 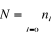 et en notant et en notant
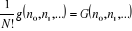 (1.7) (1.7)
L'équation (1.6) prend de la forme :
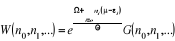 (1.8) (1.8)
| 


