CHAPITRE II: CALCUL DE LA
FLUCTUATION DU NOMBRE DE REMPLISSAGE DES NIVEAUX ENERGETIQUES POUR UN GAZ
PARFAIT QUANTIQUE EN UTILISANT LA DISTRIBUTION GRAND CANONIQUE DE GIBBS
II.1. Calcul de la valeur moyenne du nombre de remplissage des
niveaux énergétiques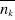 , pour un gaz parfait quantique , pour un gaz parfait quantique
A l'aide de l'expression (1.8), on peut
calculer les valeurs de n'importe quelle fonction des nombres de remplissages
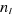 si on connaît si on connaît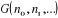 . On peut par exemple calculer : . On peut par exemple calculer :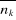 , , 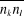 , , 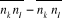 , , 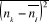 . .
Pour la raison de commodité, nous allons utiliser
l'astuce mathématique suivant : nous allons considérer comme
si le gaz parfait ne possède pas un seul potentiel chimique u mais tout
un ensemble de potentiels chimiques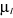 . A la fin des calculs, nous allons supposer que tous les
potentiels chimiques ul sont les mêmes et sont égaux
à u. Donc nous pouvons écrire à partir de l'expression
(1.8) . A la fin des calculs, nous allons supposer que tous les
potentiels chimiques ul sont les mêmes et sont égaux
à u. Donc nous pouvons écrire à partir de l'expression
(1.8)
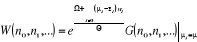 (2.1) (2.1)
La condition de normalisation conduit
à :
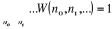 (2.2) (2.2)
C'est-à-dire :
 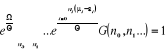 (2.3) (2.3)
En posant
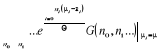 (2.4) (2.4)
L'équation (2.3) prend de la forme :
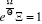 ou ou 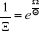 (2.5) (2.5)
et nous obtenons :
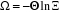 (2.6) (2.6)
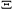 est la fonction de partition grand canonique ou somme des états
quantique ou somme statistique pour un système à nombre variable
de particules. est la fonction de partition grand canonique ou somme des états
quantique ou somme statistique pour un système à nombre variable
de particules.
En mettant l'équation (2.4) dans l'équation
(2.6) puis en dérivant l'équation (2.6) par rapport à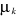 , nous arrivons à la valeur du nombre de remplissage , nous arrivons à la valeur du nombre de remplissage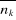 . .
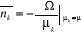 (2.7) (2.7)
L'équation (2.7) représente la valeur moyenne du
nombre de remplissage des niveaux énergétiques. Le calcul concret
de 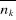 en utilisant la formule (2.7) nécessite une connaissance
précise de la grandeur en utilisant la formule (2.7) nécessite une connaissance
précise de la grandeur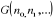 . .
Un gaz parfait quantique de particules identiques peut
être constitué, soit par les particules avec spin demi-entier
appelées fermions, soit par les particules de spin
entier appelées bosons.
Pour les fermions est valable le principe d'exclusion de
Pauli : deux ou plusieurs particules identiques ne peuvent pas se trouver
exactement dans un même état quantique. Ce fait peut être
considéré de la façon suivante. Il faut poser
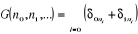 (2.8) (2.8)
Dans ce cas :
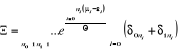  (2.9) (2.9)
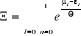
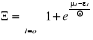 (2.10) (2.10)
D'où 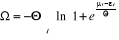 (2.11) (2.11)
Le nombre moyen de remplissage des niveaux
énergétiques est obtenu en remplaçant l'expression (2.11)
dans l'équation (2.7), ce qui donne :
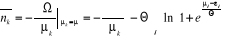
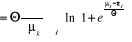 (2.12) (2.12)
Comme la dérivé de la somme est égale
à la somme des dérivés, l'expression (2.12) peut
s'écrire :
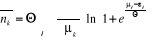
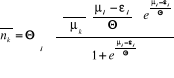
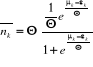
En posant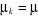 , on obtient : , on obtient :
 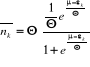 (2.13) (2.13)
En multipliant le dénominateur et le numérateur
de l'expression (2.13) par 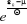 , on obtient : , on obtient :
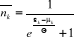 (2.14) (2.14)
Avec 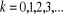
L'expression (2.14) c'est le nombre moyen de remplissage des
niveaux énergétiques pour un gaz parfait constitué par les
particules avec un spin demi-entier.
Dans le cas des bosons, il faut poser
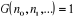 (2.15) (2.15)
ce qui va nous conduire à la statistique de Bose
Einstein, dans ce cas :
 (2.16) (2.16)
Avec 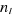 quelconque : quelconque : 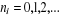 et et 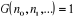
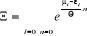
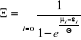 (2.17) (2.17)
Ce qui conduit à :
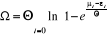 (2.18) (2.18)
En remplaçant l'expression (2.18) dans l'expression
(2.7), nous obtenons :
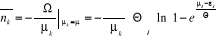
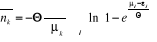 (2.19) (2.19)
Comme la dérivé de la somme est égale
à la somme des dérivés, l'expression (2.19) peut
s'écrire comme suit :
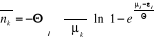
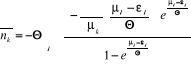
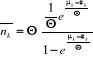
En posant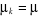 , on obtient : , on obtient :
 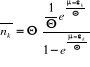 (2.20) (2.20)
En multipliant le dénominateur et le numérateur
de l'expression (2.20) par 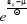 , on obtient : , on obtient :
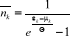 (2.21) (2.21)
Avec 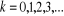
L'expression (2.21) n'est rien d'autre que le nombre moyen de
remplissage des niveaux énergétiques pour un gaz parfait
quantique constitué par les particules de spin entier.
A la limite, lorsque 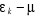 >>È, de (2.14) et (2.21) on trouve : >>È, de (2.14) et (2.21) on trouve :
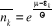 (2.22) (2.22)
Les formules (2.14), (2.21) et (2.22) peuvent s'écrire
sous la forme unique suivante :
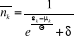 (2.23) (2.23)
où 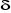 est une constante, qui est égale soit : est une constante, qui est égale soit :
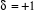 pour un gaz parfait de Fermi, pour un gaz parfait de Fermi,
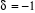 pour un gaz parfait de Bose, pour un gaz parfait de Bose,
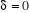 pour un gaz parfait de Boltzmann [1], [2] et [5]. pour un gaz parfait de Boltzmann [1], [2] et [5].
| 


