Section 4 :
Méthodologie de l'étude
§.1- Présentation générale
Dans le cadre de l'examen de l'évolution
des recettes issues des secteurs éducation et santé,
nous procèderons à des analyses descriptives, en faisant
ressortir à chaque fois les éléments des contextes
institutionnel et réglementaire qui peuvent avoir eu une influence sur
les variations observées. Nous examinerons aussi le poids de ces deux
secteurs dans le total annuel des recettes de services au cours de la
période considérée.
Pour la construction d'un modèle de prévision,
nous utiliserons la méthode de Box et Jenkins. Mais avant d'y arriver,
nous allons étudier puis estimer la composante tendance
déterministe et la composante saisonnière, au cas où elles
existent, tout en déterminant le schéma de décomposition
de la série concernée. L'estimation de la fonction classique qui
sous-tend l'évolution de la série (tendance déterministe)
se fera à l'aide de la régression, tandis que la
saisonnalité sera évaluée par la méthode des
moyennes mobiles.
§.2- Vérification
de l'hypothèse de stationnarité
L'étape préalable à l'utilisation de la
méthode de Box et Jenkins est de représenter graphiquement la
série temporelle afin d'avoir une indication sur la présence
éventuelle des composantes déterministes que sont la tendance
déterministe et la saisonnalité.
La vérification de cette hypothèse peut se
faire par l'examen du corrélogramme de la série ou
l'application des tests de la racine unitaire tels que les tests de Dickey et
Fuller.
1. L'examen du corrélogramme de la
série
Sur le corrélogramme simple de la série, le
phénomène de non stationnarité se traduit par des valeurs
de l'estimation 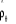 de de 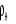 assez proches les unes des autres sans décroissance rapide. assez proches les unes des autres sans décroissance rapide.
2. Les tests de Dickey-Fuller
Les tests de racine unitaire de Dickey-Fuller permettent de
détecter le type de non stationnarité d'un processus et donc de
déterminer la bonne manière de le stationnariser.
Les modèles servant à la réalisation de
ce test sont au nombre de trois. Le principe du test est le suivant: si
l'hypothèse H0 : Non stationnarité DS (ou encore
= 0) est retenue dans l'un des trois modèles ci-dessous, le
processus est alors non stationnaire. L'hypothèse alternative est
H1 : < 0.
Modèle 1 : 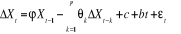
Modèle 2 : 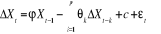
Modèle 3 : 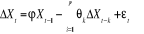
Sous H0, les règles habituelles de
l'inférence statistique ne peuvent pas être appliquées pour
tester ces hypothèses ; en particulier la distribution de Student
du paramètre ainsi que celle des paramètres b et c des
modèles servant aux tests ; Dickey et Fuller ont donc
étudié la distribution asymptotique des estimateurs de , b et c
sous l'hypothèse H0, et ont tabulé des valeurs
critiques qui sont utilisées dans ces tests.
La valeur optimale de p pour la réalisation de ces
tests peut être déterminée par analyse de la fonction
d'autocorrélation partielle de la série
différenciée ou par minimisation des critères
d'information tels que ceux d'Akaike et de Schwarz.
Notons que ces tests sont réalisés du le
modèle le plus général (modèle 1) au modèle
immédiatement le moins général selon la
significativité des paramètres.
| 


