1.2 Techniques de Calcul "Intelligent"
Le principe de base des méthodes de Calcul
"Intelligent" consiste à considérer les êtres vivants comme
modèles d'inspiration, le but étant de simuler à l'aide
des machines leur comportement.
En général, ces techniques peuvent être
regroupées en trois grandes classes : les réseaux de neurones
artificiels qui utilisent l'apprentissage pour résoudre des
problèmes complexes tels que la reconnaissance des formes ou le
traitement du langage naturel, la logique floue utilisée dans des
applications d'intelligence artificielle, dans lesquelles les variables ont des
degrés de vérité représentés par une gamme
de valeurs situées entre 1 (vrai) et 0 (faux), et les méthodes de
calcul évolutif pour la recherche et l'optimisation (figure 1.1). Ces
différentes classes seront présentées dans les sections
suivantes.







FIG. 1.1 - Techniques de calcul "Intelligent"
1.2.1 Les réseaux de neurones (Neural Networks)
Un réseau de neurones (Artificial Neural Network) est
un modèle de calcul dont la conception est schématiquement
inspirée du fonctionnement de vrais neurones. Les réseaux de
neurones sont généralement optimisés par des
méthodes d'apprentissage de type statistique, si bien qu'ils sont
placés d'une part dans la famille des applications statistiques, qu'ils
enrichissent avec un ensemble de paradigmes permettant de générer
de vastes espaces fonctionnels, souples et partiellement structurés, et
d'autre part dans la famille des méthodes de l'intelligence artificielle
qu'ils enrichissent en permettant de prendre des décisions s'appuyant
d'avantage sur la perception que sur le raisonnement logique formel.
Ce sont les deux neurologues Warren McCulloch et
Walter Pitts [McCulloch et Pitts, 1943] qui ont mené les
premiers travaux sur les réseaux de neurones. Ils constituèrent
un modèle simplifié de neurone biologique communément
appelé neurone
formel. Ils montrèrent également
théoriquement que des réseaux de neurones formels simples peuvent
réaliser des fonctions logiques, arithmétiques et symboliques
complexes.
La fonction des réseaux de neurones formels à
l'instar du modèle vrai est de résoudre divers problèmes.
A la différence des méthodes traditionnelles de résolution
informatique, on ne doit pas construire un programme pas à pas en
fonction de la compréhension de celui-ci. Les paramètres les plus
importants de ce modèle sont les coefficients synaptiques. Ce sont eux
qui construisent le modèle de résolution en fonction des
informations données au réseau. Il faut donc trouver un
mécanisme, qui permet de les calculer à partir des grandeurs
acquises du problème, c'est le principe fondamental de l'apprentissage.
Dans un modèle de réseau de neurones formels, apprendre, c'est
d'abord calculer les valeurs des coefficients synaptiques en fonction des
exemples disponibles. La structure d'un réseau de neurones artificiel
est donnée par la figure (1.2).
Le neurone calcule la somme de ses entrées puis cette
valeur passe à travers la fonction d'activation pour produire sa sortie.
La fonction d'activation (ou fonction de seuillage) sert à introduire
une non linéarité dans le fonctionnement du neurone.

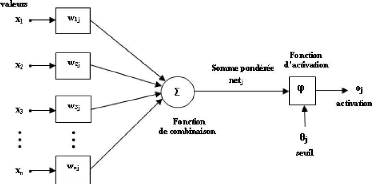
FIG. 1.2 Structure d'un neurone artificiel
Les fonctions de seuillage présentent
généralement trois intervalles :
1. en dessous du seuil, le neurone est non-actif (souvent dans
ce cas, sa sortie vaut 0 ou 1),
2. au voisinage du seuil, une phase de transition,
3. au-dessus du seuil, le neurone est actif (souvent dans ce
cas, sa sortie vaut 1).
En général, un réseau de neurone est
composé d'une succession de couches dont chacune prend ses
entrées à partir des sorties de la couche
précédente. Chaque couche i est composée de
Ni neurones, prenant leurs entrées sur les
Ni_1 neurones de la couche précédente. A
chaque synapse est associé un poids synaptique, de sorte que les
Ni_1 sont multipliés par ce poids, puis
additionnés par les neurones de niveau i, ce qui est
équivalent à multiplier le vecteur d'entrée par une
matrice de transformation. Mettre l'une derrière l'autre, les
différentes couches d'un réseau de neurones, reviendrait à
mettre en cascade plusieurs matrices de transformation et pourrait se ramener
à une seule matrice, produit des autres, s'il n'y avait à chaque
couche, la fonction de sortie qui introduit une non linéarité
à chaque étape. Ceci montre l'importance du choix judicieux d'une
bonne fonction de sortie : un réseau de neurones dont les sorties
seraient linéaires n'aurait aucun intérêt.
Plusieurs types de réseaux de neurones ont
été reportés dans la littérature, notamment le
perceptron proposé par Rosenblatt [Rosenblatt, 1958], les cartes
autoorganisatrices de Kohonen [Kohonen, 1989], le modèle neural-gas
[Martinez et Schulten, 1991] et les réseaux basés sur le
modèle de Hopfield [Hopfield, 1982], etc, [Jedra, 1999].
Grâce à leur capacité de classification et
de généralisation, les réseaux de neurones sont
généralement utilisés dans des problèmes de nature
statistique, tels que la classification automatique, reconnaissance de motif,
approximation d'une fonction inconnue, etc.
| 


