4.4 Optimisation multiobjectif par essaims
particulaires
Il est évident que l'algorithme original PSO doit
être modifié pour être adapté à la
résolution des problèmes d'optimisation multiobjectifs. Comme on
a vu, l'ensemble des solutions d'un problème avec multiples objectifs ne
se compose pas d'une seule solution (comme dans l'optimisation globale).
Cependant, dans l'optimisation multiobjectif, il est
nécessaire de trouver un ensemble de solutions (l'ensemble
Pareto-optimal). Généralement pour résoudre un
problème multiobjectif, il y' a trois objectifs principaux à
réaliser [Zitzler et al, 2000] :
1. Maximiser le nombre des éléments de l'ensemble
Pareto-optimal trouvé.
2. Minimiser la distance entre le front de Pareto trouvé
par l'algorithme et le vrai (global) front de Pareto (supposant qu'on connait
son endroit).
3. Maximiser la répartition des solutions
trouvées, de sorte que nous puissions avoir une distribution des
vecteurs la plus uniforme.
Etant donné la structure de la population de PSO, il
est souhaitable de produire plusieurs (différentes) solutions
non-dominées avec une seule itération. Ainsi, comme avec tout
autre algorithme évolutionnaire, les trois questions posés lors
de l'adaptation de PSO à l'optimisation multiobjectif sont [Coello et
al, 2002] :
1. Comment choisir les particules (employées comme leader)
afin de donner plus de préférence aux solutions
non-dominées.
2. Comment maintenir les solutions non-dominées
trouvées pendant le processus de recherche afin de rapporter les
solutions non-dominées, en tenant compte de toutes les anciennes
populations et non seulement de la population courante. Aussi, il est
souhaitable que ces solutions soient bien réparties sur le front de
Pareto.
3. Comment maintenir la diversité dans l'essaim afin
d'éviter la convergence prématurée vers une seule
solution.
Comme nous l'avons déjà vu, en résolvant
les problèmes d'optimisation à un seul objectif, pour chaque
particule, le leader qui a la meilleure des meilleures performances dont elle a
connaissance, est complètement déterminé une fois une
topologie de voisinage est établie. Cependant, dans le cas des
problèmes d'optimisation multiobjectif, chaque particule pourrait
communiquer avec différents leaders, un seul étant choisi afin de
mettre à jour sa position. Un tel ensemble de leaders est habituellement
stocké dans une mémoire appelée archive externe. Les
solutions contenues dans les archives externes sont employées comme
leaders quand les positions des particules de l'essaim doivent être mises
à jour. En outre, le contenu des archives externes est souvent
rapporté comme résultat final de l'algorithme.
L'algorithme général de MOPSO est décrit
par le pseudo code (6). Nous avons marqué en italique les processus qui
rendent cet algorithme différent de l'algorithme PSO de base de
l'optimisation à un seul objectif.
algorithme 6 Pseudo code de l'algorithme général de
MOPSO
Initialiser l'essaim
Initialiser l'ensemble de leaders
mesurer la qualité de leaders
t 4-- 0
tant que (t < tmax)
Pour chaque particule
Sélectionner un leader
Calculer la vitesse
Mettre à jour la position
Effectuer la mutation si c'est nécessaire Mettre
à jour pbest
Fin pour
Mettre à jour les leaders dans l'archive externe
mesure la qualité de leaders
t 4-- t + 1
Fin tant que
Retourner les résultats de l'archive externe
Après l'initialisation de l'essaim, un ensemble de leaders
est également initialisé avec les particules non-dominées
de l'essaim. Comme nous avons déjà mentionné,
l'ensemble de leaders est souvent stocké dans des
archives externes. Ensuite, une mesure de qualité est calculée
pour tous les leaders afin de choisir (souvent) un leader pour chaque particule
de l'essaim. A chaque génération, pour chaque particule, un
leader est choisi et le vol est exécuté. La plupart des MOPSOs
existants applique un opérateur de mutation après
l'exécution du vol. La particule est ensuite évaluée et la
valeur de pbest (la meilleure position qu'elle a atteinte jusqu'ici)
correspondante est mise à jour. Une nouvelle position de particule
remplace sa pbest habituellement quand cette position de particule domine sa
pbest ou si elles sont toutes les deux non-dominée l'une de l'autre.
Après la mise à jour de toutes les particules, l'ensemble de
leaders est mise à jour aussi. Finalement, la mesure de qualité
de l'ensemble de guides est recalculée. Ce processus est
répété pour un certain nombre d'itérations.
En résumé, pour adapter l'algorithme de base PSO
à la résolution des problèmes multiobjectifs, on est
confronté à deux difficultés majeures [Pulido, 2005] :
1. Choix et mise à jour des leaders
- Comment choisir un seul guide de l'ensemble des solutions
non-dominées qui sont toutes bonnes, on peut le choisir d'une
manière aléatoire ou on doit utiliser un critère
additionnel (pour favoriser la diversité, par exemple).
Comment choisir les particules qui devraient demeurer dans les
archives externes d'une itération à l'autre.
2. Création de nouvelles solutions
Comment favoriser la diversité en utilisant deux
mécanismes pour créer de nouvelles solutions : mise à jour
de positions et mutation. Ces concepts sont discutés en détail
dans les prochains paragraphes.
4.4.1 Leaders dans l'optimisation multiobjectif
Puisque la solution d'un problème multiobjectif se
compose d'un ensemble de bonnes solutions, il est évident que le concept
de leader traditionnellement adopté dans PSO doit être
changé. Afin d'éviter la définition d'un nouveau concept
de leader pour des problèmes multiobjectifs, certaines méthodes
utilisent des fonctions d'agrégation (sommes pondérées des
objectifs) ou approches qui optimisent chaque objectif
séparément. Cependant, il est important d'indiquer que la
majorité des approches actuellement proposées de MOPSO
redéfinissent le concept de leader.
Comme mentionné plus haut, le choix d'un leader est une
composante importante dans la conception de MOPSO. L'approche la plus directe
est de considérer chaque solution non-dominée comme un nouveau
leader et puis, un seul leader étant choisi. De cette façon, une
mesure de qualité qui indique la qualité d'un leader est
très importante. Evidemment, une telle approche peut être
définie de différentes manières. Des différentes
propositions, pour traiter ce problème, seront présentées
plus loin.
Une manière possible de définir une telle mesure
de qualité peut être les mesures de densité. La promotion
de la diversité peut être faite par ce processus au moyen de
mécanismes basés sur quelques mesures de qualité qui
indiquent la proximité des particules dans l'essaim. Plusieurs auteurs
ont proposé des techniques de choix de leader qui sont basées sur
des mesures de densité, nous présentons ici deux des plus
important mesures de densité utilisées dans le domaine de
l'optimisation multiobjectif :
- Estimateur de densité de voisin le plus proche :
L'estimateur de densité de voisin le plus proche nous donne une
idée de la façon dont les voisins les plus proches d'une
particule donnée sont distribués, dans l'espace de fonction
objectif [Deb et al, 2002]. Cette mesure estime le périmètre du
cuboïde formé en employant le plus proche voisin comme sommet
(figure 4.5).
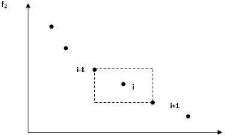
FIG. 4.5 - Exemple d'estimateur de densité de voisin le
plus proche
- Estimateur de densité de grain: Quand une particule
partage les ressources avec d'autres particules, sa fitness est
dégradée proportionnellement au nombre et proximité des
particules qui l'entourent avec un certain périmètre seuil
[Goldberg et Richardson, 1987; Deb et Goldberg, 1989]. Un voisinage d'une
particule est défini en termes de paramètre noté
óshare qui indique le rayon de voisinage. De tels
voisinages s'appellent niches écologiques (figure 4.6).
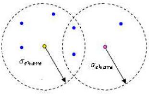
FIG. 4.6 Niches de particules
| 


