INTRODUCTION
L
ES VAGUES et la mer en général, ont toujours
exercé un mystérieux attrait sur les hommes. Et malgré
cette apparente monotonie, nous
avons beaucoup de mal à comprendre leur naissance et leur
évolution. Ainsi le mécanisme de vague s'est progressivement
laissé découvrir ce dernier siècle après
d'instantes recherches faites de façon complémentaire par les
physiciens et les mathématiciens qui se sont succédés
jusqu'à nos jours. Ces derniers ont montré que c'est l'action du
vent à la surface de l'eau qui est responsable de la formation de ces
vagues obéissant aux mêmes règles depuis des
millénaires interpellant navigateurs et chercheurs.
Une vague est une onde mécanique qui se propage
à la surface de l'eau entre deux fluides en l'occurence l'eau et
l'air.
Depuis les travaux de Kelvin [1], de noubreuses contributions
et simulations numériques ont été publiées pour la
modélisation des vagues de surface. Dans la plupart d'entre eux, les
auteurs [3,4] considèrent que la capillarité est
négligeable par rapport aux forces en présence à la
surface de la mer.
Malheureusement, comme il a été souligné
dans les articles [9] et par d'autres auteurs[5], que le modèle est mal
posé dans le sens oil l'existence d'ondes à la surface de l'eau
est due d'une part à la pesanteur qui tend à maintenir
l'interface air-eau horizontale (ondes de gravité) et d'autre part
à la tension de surface qui tend à maintenir l'interface plane
(ondes capillaires).
Dans ce document, nous considérons d'une part un
écoulement capillaire possédant une surface libre dans un domaine
incluant un sous-marin et d'autre part, nous-nous intéressons à
la propagation acoustique dans ce domaine contenant l'eau en écoulement
uniforme et soumis à de petites perturbations autour d'un
écoulement moyen initial réalisant l'équilibre statique de
la surface libre.
Bien qu'étant à la base de la majorité
des modèles présents dans la littérature, l'étude
de la propagation acoustiques dans des écoulements reste un
problème d'actualité et difficile à appréhender
dont les principales applications se rencontent dans les secteurs de
l'industrie maritime et de l'aéronautique.
En se limitant au cadre de la propagation linéaire dans
un domaine con-tenant un sous-marin en présence d'un écoulement,
nous nous sommes proposé d'étudier l'acoustique sous-marine qui a
pour objet l'étude et l'utilisation de modèles
mathématiques décrivant la propagation des ondes acoustiques dans
la mer.
Pour le modèle de surface, il est connu que dans le
cadre linéaire simple des ondes progressives dans un domaine
borné modélisé par le modèle de Neumann-Kelvin des
instabilités numériques apparaissent. Ainsi, nous avons choisi de
prendre comme modèle d'ondes progressives à la surface de la mer,
le modèle traduisant l'équilibre de la surface libre en
présence de la tension superficielle et de la gravité.
Modèle défini dans l'article de Philippe Destuynder et Caroline
Fabre [9].
Par ailleurs, les problèmes de propagation d'ondes sont
souvent posés en domaine non borné et une des questions
importantes pour leur résolution numérique est de savoir borner
artificiellement le domaine de calcul. Afin de construire ces limites
articielles de sorte que le problème aux conditions initiales et aux
limites soit "bien-posé" et que les frontières latérales
du domaine soient "transparentes" vis-a-vis des ondes entrantes et sortantes,
B. Engquist et Majda (1977) ont mis au point une méthode
théorique pour rendre les limites transparentes à un niveau
d'approximation clairement défini.
Leur théorie générale de construction des
conditions transparentes s'appuie sur l'analyse modale des équations du
mouvement linéarisées autour d'un état de
référence et ré-écrites aux bords sous la forme
d'une condition qui peut en général s'exprimer à l'aide de
l'opérateur de DirichletNeumann. En générale, la forme de
cette opérateur n'est pas toujours commode (pratique), l'essentiel du
travail de construction des conditions transparentes consiste donc à
trouver une bonne approximation de ce dernier.
Dans ce travail, un autre thème important abordé
dans ce travail est celui du traitement des conditions aux limites non
réfléchissantes (ou transparentes) pour l'acoustique en
écoulement.
Celles-ci sont à la fois indispensables du fait du
caractère nécessairement borné du domaine de calcul et
cruciales pour l'obtention de résultats numériques pertinents.
Ces conditions transparentes doivent être en mesure de
simuler une condition de rayonnement à l'infini, tout en veillant
à ne pas créer de réflection aux frontières du
domaine de calcul.
Ce sujet reste aujourd'hui un important axe de recherche dans
l'étude et la simulation numérique de l'ensemble des
phénomènes de propagation d'ondes.
La méthode des équations intégrales qui
est utilisée par la plupart des codes de calcul industriels, ne permet
pas de traiter ces aspects de façon satisfaisante et nécessitent
des hypothèses simplificatrices incompatibles avec une
représentation réaliste des phénomènes physiques en
présences. Les difficultés sont multiples : d'une part le
modèle linéaire est naturellement instable et seul la
présence de termes non linéaires à la surface de l'eau
permet de la stabiliser et d'autre part, il apparait trois types d'ondes
couplés (ondes de gravité, ondes acoustiques et ondes de
capillarité ).
La grande disparité des vitesses d'ondes et de celle du
sous-marin conduisent à des difficultés numériques qu'il a
fallu surmonter en utilisant un schéma d'intégration en temps
adapté et qui ne dissimule pas l'un des phénomènes en
présence.
La pertinence de ce travail est justifiée en particulier
par la construction
3
d'un modèle de condition aux limites transparentes
évitant les réflexions d'ondes.
Ce mémoire s'articule autour de six chapitres suivant les
points d'étude précedemment évoqués.
Ainsi, dans le deuxième chapitre nous
définissons les modèles, présentons les lois physiques et
les principales hypothèses permettant d'aborder le problème et
nous donnons les équations gouvernant les écoulements
considéres.
Le principal résultat de ce chapitre est
l'écriture mathématique de la condition aux limites transparentes
sur les frontières représentant respectivement la section
d'entrée du fluide et la section de sortie du fluide. Cette condition
aux limites est obtenue et est valable seulement pour les frontières
planes perpendiculaires à la direction de l'écoulement.
Une validation numérique sur un cas test (dimension 1) de
cette condition aux limites est effectuée afin de vérifier
l'efficacité de la méthode.
Le troisième chapitre est consacré à
l'étude des différentes formulations variationnelles et au
modèle couplé fluide-vague à la surface. Pour cet
étude, nous-nous sommes intéressé à la
determination d'une nouvelle frontière du domaine.
Il s'agit de frontières adaptées évitant des
ondes tangentielles à la frontière qui diffracteraient.
Nous proposons aussi dans ce chapitre une étude du
système couplé approché obtenu afin d'établir des
résultats d'existence, d'unicité et de stabilité a
priori du modèle. Nous déduisons de cette étude qu'en
présence d'une capillarité, nous avons une vitisse critique,
vitesse au dessus de laquelle le modèle peut être instable.
Dans le quatrième chapitre, nous présentons les
logiciels et la méthode numérique utilisés. La
méthode numérique appropriée pour la prise en compte des
conditions aux limites que nous avions choisi est celle des
éléments finis.
Le cinquième et le sixième chapitres sont
consacrés à la vérification numériques de la
validité du modèle numérique présenté dans
le quatrième chapitre.
L
'ouvERt tridimensionnel sur lequel est posé le
problème d'écoulement sera noté Ù ?
R3. Il correspond à un bassin rempli d'eau
dans
lequel un corps immergé est animé d'un mouvement
rectiligne uniforme. Pour la mise en équation, on se placera dans le
référentiel lié au corps, cela revient à supposer
qu'il est fixe et soumis à un écoulement que l'on supposera
uniforme et irrotationel. La vitesse à l'infini amant est u.
Notons que la frontière de ce bassin est
partitionnée en cinq parties:
- une surface libre notée s,
- le fond du bassin que l'on note 0, est supposé
imperméable, - deux côtés latéraux 1 et 2 par
lesquels l'eau rentre et sort, - et b la surface arbitraire entourant
le corp immergé (un sous-marin)
et ne rencontrant pas la surface libre.
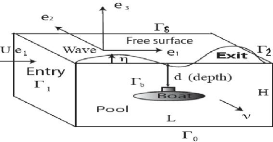
FiGuRE 2.1 - Modèle.
Afin de bien rendre compte de l'intéraction
fluide-modèle de vague, nous allons analyser séparément
les équations régissant le comportement du fluide dans le bassin
et celles qui régissent celui de la surface libre en prenant en compte
l'effet de la capillarité .
Ensuite, une formulation mathématique et physique des
conditions aux limites transparentes sera faite pour les frontières
latérales entrante 1 et sortante 2 .
Nous ferons des hypothèses classiques permettant de
construire un modèle sur lequel il est possible d'obtenir de nombreux
résultats opérationnels. On suppose que :
1. le fluide est parfait et compressible et il n'est soumis
qu'à des forces de gravité et de pression.
2. Le champ de vitesses u des particules fluides est
supposé irrotationnel :
rot(u) = 0,
et la circulation du champ de vitesses sur chaque composante
connexe de la frontière de l'ouvert occupé par le fluide est
supposée nulle.
Ceci permet d'assurer l'existence d'une fonction potentielle de
vitesses notée ö définie à une constante
additive près telle que :
u = Vö.
2.1 MoDèle DANs l'eAu
Etant donné ñe la masse
volumique de l'eau, le principe de conservation de la masse (2.7.1)
s'écrit :
?ñe
?t +
div(ñeVö) = 0 dans n×]0,
T[. (2.1)
L'équation traduisant le théorème de la
conservation de la quantité de mouvement s'écrit :
?u
ñe( ?t + uvu) =
ñeg - Grp dans n×]0, T[. (2.2)
Afin de simplifier cette relation et de trouver une
intégrale première, nous introduisons un potentiel de barotropie
notée F(ñe) et qui est défini
par : F(ñe) = fe ñe 1
?p 0 ñ ?ñe(ñe)dñ +
c(x), (2.3)
d'où
|
?F 1 ?p
rF(ñe) =
.rñe + rc = . ?ñe
(ñe).rñe
?ñe ñe
Vp
|
+Vc,
|
Par conséquent, le gradient de (2.3) est donné par
:
1
VF(ñe) =
.rp(ñe) + rc (2.4)
ñe
En négligeant la gravité dans (2.2), et en
tenant compte de l'hypothèse de fluide non visqueux, on obtient une
formulation plus simple de la relation fondamentale :
?ö 1
v ( ?t + 2
|Vö|2 + F(ñe)) =0
dans n×]0, T[. (2.5)
Et comme le potentiel des vitesses ö est
définie à une constante spatiale additive près, en
choisissant convenablement cette constante on obtient :
?ö +
?t 2 |Vö|2 +
F(ñe) = 0 dans n×]0, T[,
(2.6a)
1
2.1.1 Hypothèses de petites pertubations
Dans le cadre de la théorie linéaire de
l'acoustique, les pertubations (pour une particule donnée à un
instant donné) des quantités caractérisant
l'écoulement sont supposées suffisamment petites pour pouvoir
limiter au premier ordre les développements (en puissances d'un
paramètre caractéristique e, sans dimension, de l'ordre
de grandeur de la pertubation et petit devant l'unité) de ces
quantités autour de l'état non pertubé.
Cette hypothèse consiste donc à envisager des
mouvements de faible amplitude autour d'un état moyen défini par
un écoulement permanent représenté par le potentiel de
?0, solution du problème de Neumann:
|
? -A?0
|
= 0 dans 1, et R 1 ?0
|
= 0,
|
|
|
?????????
|
|
|
|
|
??0
|
= 0 sur F0 ? Fb ? Fs,
|
|
(2.7)
|
|
?í
|
|
?????????
??0
|
= u(e1, í) sur F1 ? F2.
|
|
|
|
?í
|
|
|
|
Dans ce système, u est l'amplitude de la vitesse
d'écoulement suivant la direction e1.
Et le champs de vitesse constant est donné par le gradient
de ?0.
D'autre part, pour des raisons de simplification, nous
supposons que ?0 est suffisament régulière et de classe
C°°(1) pour justifier les calculs dans la
suite.
Nous écrivons ensuite :
Equation traduisant la conservation de la
masse
La linéarisation de l'équation de continuité
(2.1) :
?ñe
ö(x, t) = ?0(x)
+ ?(x, t), ñe(x,
t) = ñ0 + ñ(x, t)
x ? R3,
?t + Vñe
·
Vö + ñeAö = 0 dans 1x]0,
T[.
autour de ?0 et ñ0 donne:
?ñ ?t + V?0
· Vñ
+ ñ0A? = 0 dans 1x]0, T[. (2.8)
|
d'ou :
|
?ñ
?t
|
= -V?0
· Vñ -
ñ0A? dans 1x]0, T[. (2.9)
|
Equation de conservation de la quantité de
mouvement
De même pour la deuxième équation du
système précédent, la linéarisation se fait en deux
étapes (cf :[10]).
- Etape 1 : On dérive par rapport au temps
l'équation (2.6a)
|
?2ö ?t2 +
|
1 ?t(|Vö|2) +
?F
? ?ñe (ñe)?ñe
?t = 0,
2
|
?F 1 ?p
?ñe (ñe) =
ñe ?ñe (ñe),
et on linéarise autour de l'état permanent :
?2? ?p
?t2 + r?0
·
r(?? ?t ) + 1 ?ñ0
(ñe)?ñ ?t = 0,
ñ0
ensuite, on remplace ?ñ par l'expression
précedente : ?t
?2, ?? 1 ?p ?p
?t; + V?0
· v( ?t
) - ñ0 ?ñe (ñ0)(V?0
· Vñ) - , (ñ0)6? =
0.
uñe
(2.10)
- Etape 2 : On applique l'opérateur
V?0V(
·) à l'équation (2.6a)
G?0
· V(?ö)
+ 1 (Gr?0
· V(|Vö|2)) +
(V?0
· V (F(ñe)) =0,
?t 2
comme
v(|vö|2) = 2V.(V?0
·
V?) et V(F(ñe) = 1 ?p
ñe ?ñe
(ñe).rñe,
alors
|
V?0
· V
(F(ñe) = ñ10
|
?p
?ñe
|
(ñ0).(V?0
·
Vñ).
|
On obtient alors la relation suivante :
r?0
· r.(?? ?t ) +
r?0
· r.(r?0
· r?)) + 1
?p
?ñe (ñ0).(rñ0
· rñ) = 0.
ñ0
(2.11) Et pour conclure, on additionne les deux relations
(2.10) et (2.11) ce qui donne alors l'équation des ondes :
?2?
?t2 + 2r?0
· r(??
?t ) + V?0
· V(V?0
· V?) - c2f6? = 0 dans
I/×]0, T[.
(2.12)
avec
?p
cf 2 = ?ñe (ñ0), vitesse
du son dans le fluide.
Modèle dans l'ouvert U.
|
- un écoulement stationnaire problème
stationnaire
? ????????? ?????????
|
: --Ä?0
??0
|
de potentiel de vitesse ?0 solution du
= 0 dans Ù,
= 0 sur 0 U b U s,
= u(e1, í) sur 1 U 2.
|
|
?í
??0
|
|
?í
|
Où ?0 est définie à constante
près, que nous fixons en prenant par exemple la condition de moyenne
nulle sur s :
Z
?0 = 0, s - et un
écoulement transitoire représenté par le potentiel ?
solution de :
?2?
?t2 +2V?0 .V.(?? ?t
)+V?0 .V(V?0 .V?)-- c2 f
Ä? = 0 dans Ùx]0, T[.
| 


