2.4 CONDITIONS AUX LIMITES TRANSPARENTES
De nombreux problèmes de propagation d'ondes se posent en
milieu
non borné ou du moins très grand par rapport
à la zone d'intérêt.
Pour des raisons pratiques évidentes, on est
amené à réduire les calculs effectifs à un domaine
borné en espace. Se pose alors le problème du traitement de la
frontière artificielle ainsi introduite afin de simuler le fait que le
milieu de propagation réel est infinie.
C'est ce qui nous amène à introduire les notions
de conditions aux limites transparentes appliquée à notre
modèle hydroacoustique.
La méthode consiste à borner latéralement
notre domaine de calcul par des frontières découpées selon
les isopotentielles sur lesquelles on écrit une condition aux limites
dite transparente, c'est-à-dire une condition exacte qui prend en compte
le comportement à l'infini des ondes sortantes sans réflexion
parasites, et qui n'influence pas la solution.
Nous traitons successivement deux cas de difficultés
croissantes dans cette section, d'abord la formulation monodimensionnelle
décrivant la condition aux limites transparentes pour la propagation des
ondes acoustiques qui est un cas classique mais dont l'étude a des
vertus pédagogiques et ensuite la généralisation en
dimension n = 2,3 de cette formulation, toujours pour les ondes
acoustiques.
2.4.1 Condition aux limites transparentes en dimension n
=1 Considerons une equation d'ondes homogène en dimension 1.
|
{
|
a2 au
at2u (x, t) --
c2f ax2
(x, t) = 0 pour x E IR et t > 0,
u(x, 0) = u0(x) pour
x E IR,
'
at
au (x 0) = u1(x)
pour x E IR.
|
(2.18)
|
On cherche la solution generale de cette equation differentielles
aux derivees partielles en effectuant le changement de variable :
|
{
|
X = x + cft,
Y = x -- cft.
|
En posant
u(x, t) = U(X,
Y),
l'equation des ondes (2.18) en variable X, Y
s'ecrit sous la forme :
Par integration, on obtient :
U(X, Y) = F(X)
+ G(Y) <=> u(x, t) =
F(x + cft) + G(x -- cft).
(2.19)
Les fonctions F et G sont arbitraires et au
moins de classe C2 et dependent du choix des conditions
initiales en vitesse, en positions et aux limites à l'infini :
on obtient le système :
|
{
|
F(x) + G(x) =
u0(x), Fi(x) --
Gi(x) = u1(x).
|
La solution du problème (2.18)avec des conditions
initiales donnees est donc la superposition de deux ondes progressives, l'une
se propageant vers la droite à la vitesse cf, l'autre vers la
gauche à la vitesse --cf. Cette solution est donnee par la
relation :
c ,. f x-t x+ t
u(x, t) = 1 [u0(x +
cf t) + u0(x -- cf t)] + ' u1
(s)ds. (2.20)
2
au
at
Nous allons maintenant etudier la façon dont l'onde
propage l'information. Pour cela, nous definissons les courbes caracteristiques
en posons : 41= --cf ax au et x =
En remplaçant dans l'équation (2.18), on obtient
:
? (ø
?t
) ? 0 cf ?
÷ + 0?
cf 0 x
) at = 0
] ,
L'équation des ondes est hyperbolique donc on peut
diagonaliser la ma-trice qui intervient dans l'équation differentielle
.
On obtient un système d'équations
différentielles découplées d'ordre 1 :
?
?
?
?t
? ?
C- ? ? ?
-cf 0 C-
?
? + ? ? ? ? = 0
C+ ?t
0 cf C+
Les vecteurs propres associés aux valeurs propres
cf et -cf sont :
|
?
v1 = ?
|
1
-cf
|
et ?
) v2 = ?cf1.
|
donc les composantes dans la bases des vecteurs propres sont :
?
??? ?
????
?u cf ?x
C+ = ?u
?t
?u
?x
?u
C- = ?t + cf
Les quantitées C- et C+ sont
conservées le long des courbes caractéristiques :
x - cft = constante et x +
cft = constante
Ce sont les quantitées entrantes et sortantes,
respectivement aux vitesses : -cf et cf au travers des
frontières lorsqu'on limite le domaine.
Conditions limites
D'après ce qui précède, C-
et C+ sont invariantes le long des courbes
caractéristiques, donc ce sont les quantités entrantes et
sortantes du domaine.
Supposons que l'on place une frontière ouverte,
c'est-à-dire transparente, en x = L (cf figure 2.2).
On se place dans l'hypothèse oil l'influence extérieure est
nulle. La quantité entrante est donc nulle :
C+ = 0,
le même raisonnement en x = -L,
mène à la condition :
C- = 0.
En tenant compte des expressions de C- et
C+ données précédemment, on obtient que
les conditions aux limites naturelles pour u pour les
frontières ouvertes sont définies par :
|
?
????
????
|
?u ?u
?t (-L, t) - cf ?x
(-L, t) = 0?uu?u
?t (L, t) + cf ?x
(L, t) = 0 '
|
(2.21)
|
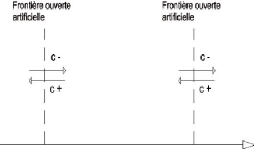

FIGURE 2.3 - Représentation des quantités
caractéristiques au travers des frontières ouvertes.
Mise en oeuvre et résultats numérique en
dimension 1
La mise en oeuvre numérique en dimension un du
problème concernant la condition aux limites transparentes est la
suivante.
Dans un premier temps, nous considérons le problème
suivant :
|
?2u
?t2 - c2 ?2u
?x2
|
= 0 xE]0, L[×]0, T[,
|
conditions initiales :
u(x,0) = u0 x E]0, L[,
?
???????????????????????? ?
?????????????????????????
?u
(2.22)
?t (x,0) = u1 x E]0, L[,
conditions aux limites :
u(0, t) = 0 ?t > 0,
?u ?u
?t (L, t) + c?x
(L, t) = 0 ?t > 0.
Ou c représente la vitesse d'onde en mètre
par seconde.
Ce problème sera mis sous sa forme variationnelle que nous
décrivons ci-après. Ensuite, nous présentons les
résultats numériques obtenus.
Formulation variationnelle
On considère l'espace :
V = {v E H1(]0,
L[), v(0) = 0}
Le problème devient après multiplication par
v :
L ?2u L ?2u
o
?x2
v(x)dx = 0,
? v ? V; f?t2
v(x)dx - c2
en intégrant ensuite par parties le deuxième terme
entre 0 et L , on obtient :
?v, at2 0 ax
fL ?2u L ?u (x'
t) J (x,t)v(x)dx +
c2 I ?u (L,
t)v(L) = 0,
0 ??v
x (x)dx c?t
On approche l'espace V par l'espace des fonctions affines par
morceaux et continues wi :
L
Vh = {wi : wi(xj)
=äij,?i = 1, ...N - 1 , ?j = 1,
...N - 1 et xj =j N } Le problème
approché dans Vh est donc :
|
trouver uh ? Vh tel que ? vh
? Vh :
L ?2uhL? ax ?x ?t ax ?vh uh
?t2 (x,
t)vh(x)dx + c2 I
(x, t) (x)dx ca
(L, t)vh(L) = 0.
o
|
Le modèle peut donc s'écrire formellement sous
forme d'une équation différentielle matricielle à
coefficients constants :
|
?????
|
trouver X(t) tel que :
M ·X(t) + C
ÿX(t) + AX(t) = 0,
|
(2.23)
|
où :
- M est une matrice de masse,
- A une matrice de raideur,
- C une matrice contenant un seul élément .
Et l'équation différentielle du second ordre
(2.23) est résolue, en introduisant un découpage en temps, ou
nAt est le pas de temps et tn =
nAt. Pour obtenir un schéma totalement
discrétisé, on approche en temps par :
- ·X(nAt) =
|
Xn+1 - 2Xn +
)0-1
At2
|
Et pour améliorer la stabilité, il est
préférable de moyenner les termes de raideur en posant :
X(nAt) = Xn+1 +
Xn
2
ce qui conduit au schéma suivant :
M Xn+1 - 2Xn
+ Xn-1 + C Xn+1 - Xn +
AXn+1 + Xn = 0, (2.24)
Ät2 Ät 2
équivalent au schéma :
Ät2
2 A]Xn+1 = [2M +
ÄtC - Ät2
[M + ÄtC + 2
A]Xn - MXn-1. (2.25)
Analyse de la stabilité
Nous ferons l'analyse de la stabilité de ce schéma
en utilisant les techniques de l'énergie.
Pour cela, nous considérons le schéma (2.24)
précedent :
Xn+1 - 2Xn +
Xn-1 Xn+1 - Xn
Xn+1 + Xn
M + C + A = 0,
Ät2 Ät 2
ce qui donne :
M( Xn+1 - Xn
Ät2 ) - M( Xn+1 - Xn
Ät2 ) + C( Xn+1 - Xn
Ät ) + A( Xn+1 + Xn
2 ) = 0
En multipliant scalairement par :
Xn+1 - Xn,
M(
Xn+1 - Xn Ät , Xn+1 -
Xn
Ät ) + 1
ÄtC(Xn+1 -
Xn, Xn+1 - Xn) +
1 2(AXn+1,
Xn+1)
= M( Xn - Xn-1
Ät , Xn+1 - Xn
Ät ) + 1
2(AXn, Xn).
(2.26)
L'inégalitée de Cauchy-Schwarz suivante :
(MX, Y)
=<12(MX,, X) +
12(MY,, Y),
appliquéee au premier terme du second membre de
l'égalitée (2.26), donne :M( Xn - Xn-1
Ät , Xn+1 - Xn
Ät ) = 1 2 M( Xn -
Xn-1
Ät , Xn - Xn-1
Ät ) t1 1Xn+1 1-
--XnnXn+1 i- --Xnn+ +2M((Ät
t, 'Ätt ),'
on obtient ensuite :
1 1(MXn+1 1-
--XnnX+1 1- _Xnn11112Ät
,
'
Ät
)
)
+
+
ÄtC(Xn+1
1
-
--
Xn,
,
Xn+1
1
-
--
2
t
t
+ 2 A(Xn+1,
Xn+1))
Xn)
)
+
11Xnn-_Xn-11Xn n-
_Xn-11=<2M((
Ät t, 'Ätt
).
·
(2.27)
Et comme la matrice C contient seulement un seul terme
positif, alors le terme suivant est positif :
Ätt
1 C(Xn+11 ---
Xn, Xn+11 ---
Xn)) => 0,
l'inégalité (2.27) donne l'inégalité
:
2 M( Xn+1 - Xn
1 Ät , Xn+1 - Xn
Ät ) + 1 2
A(Xn+1, Xn+1) =1 2 M(
Xn - Xn-1
Ät , Xn - Xn-1
Ät )
+ 2 A(Xn,
Xn).
1
On définit l'énergie mécanique par:
1 Ät , Xn - Xn-1
En = 2 M( Xn - Xn-1
Ät ) + 1 2 A(Xn,
Xn),
d'où
En+1 = En.
L'énergie mécanique totale est
décroissante au sens large au cours du temps, ce qui assure la
stabilité de ce schéma numérique dès que la
solution est elle-même stable.
Résultats numériques
Pour cette application numérique, nous
considérons une onde se propageant sur un segment de longueur L
= 10 m, que nous maillons en 250 points.
La célérité de l'onde est égale c
= 340 m/s.
Les figures suivantes représentent la solution
numérique du modèle (2.29) qui est une onde progressive.
Dans cet exemple, la condition aux limites est appliquée
sur la frontière
représentant la section de sortie du fluide
afin de vérifier sa transparence,
dans le sens où celle ci
laisse sortir les ondes et ne provoque pas de retours.
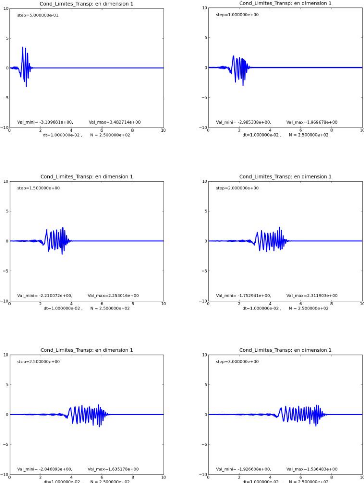
Sur ces figures, nous avons l'onde longitudinale se propageant
vers la frontière droite. Sur cette frontière, nous avons
défini une condition aux limites transparentes pour laisser sortir
l'onde sans réflexion parasite.
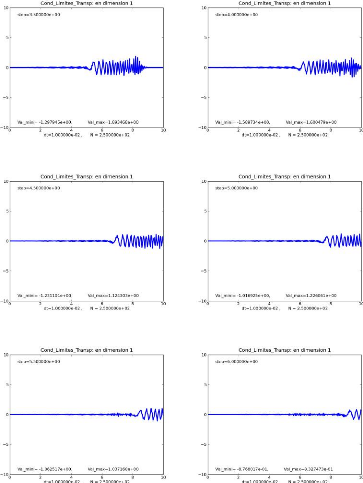
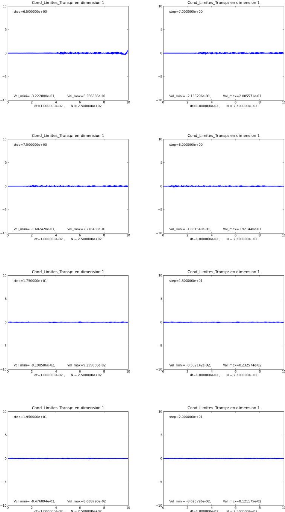
Les figures suivantes confirment bien le caractère
transparent de cette condition.
| 


