III.2. CLASSIFIEUR BAYESIEN [1,
5, 14]
III.2.1 RAPPELS SUR LA
STATISTIQUE
III.2.1.1 Notions de probabilité
Il existe plusieurs manières de définir une
probabilité. Principalement, on parle de probabilité inductive ou
expérimentale et de probabilités déductives ou
théoriques. On peut les définir comme suit :
Ø Probabilité expérimentale ou
inductive : la probabilité est déduite de toute la
population concernée. Par exemple, si sur une population d'un million de
naissances, on constate 530 garçons et 470 filles, on dit que
P[garçons]=0.53
Ø Probabilité théorique ou
inductive : cette probabilité est connue grace à
l'étude du phénomène sous-jacent sans
expérimentation. Il s'agit donc d'une connaissance à priori par
opposition à la définition précédente qui faisait
plutôt référence à une notion de probabilité
à posteriori. Par exemple, dans le cas classique du dé parfait,
on peut dire sans avoir à jeter un dé, que P[Obtenir un
4]=1/6.
Comme il n'est pas toujours possible de déterminer des
probabilités à priori, on est souvent amené à
réaliser des expériences. Il faut donc pouvoir passer de la
première à la deuxième solution. Ce passage est
supposé possible en termes de limite.
III.2.1.2 Épreuve et
Evénement
Une expérience est dite aléatoire si ses
résultats ne sont pas prévisibles avec certitude en fonction des
conditions initiales.
On appelle épreuve la réalisation d'une
expérience aléatoire, on appelle événement la
propriété du système qui une fois l'épreuve
effectuée est ou n'est pas réalisée.
III.2.1.3 Espace probabilisable, Espace
probabilisé
Une expérience aléatoire définit un
ensemble d'événements possibles ? appelé univers.
Définition : on appelle
tribu sur ? tout sous-ensemble ? de P(?) tel que :
1. ?   ? ?
2. Si A  ? alors ? alors   ? ?
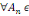 3. 3. 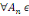 ?, on a ?, on a 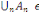 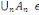 ? ?
(?   ?) est un espace probabilisable ?) est un espace probabilisable
Définition :
Soit (?   ?) est un espace probabilisable. On appelle probabilité sur (? ?) est un espace probabilisable. On appelle probabilité sur (?
  ?) toute application P de ? dans [0,1] telle que ?) toute application P de ? dans [0,1] telle que
1. P(?)=1
2. Pour toute famille (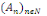 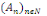 d'élément deux à deux disjoint de F, on a : d'élément deux à deux disjoint de F, on a :
P(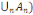 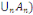 = =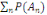 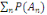 (?, ?,P) est un espace probabilisé (?, ?,P) est un espace probabilisé
P est appelée loi de probabilité
Si ? est fini, la tribu ? est le plus souvent égale
à l'ensemble des parties de ?
Propriétés
élémentaires
De l'axiomatique de Kolmogorov, on peut déduire les
propriétés suivantes :
1. P (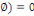 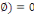
2. P (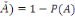 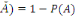
3. P(A)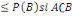 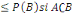
4. P(A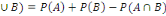 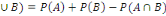
5. P (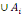 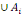 ) )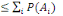 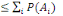
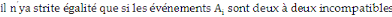
III.2.1.4 Probabilité
conditionnelle
Soient deux événements A et B
réalisés respectivement n et m fois au cours de N
épreuves. On a donc P(A)=n/N et P(B)=m/N. si de plus A et B sont
réalisés simultanément k fois, on a P(A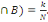 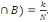 Que peut-on déduire sur la probabilité de
l'événement B sachant que l'événement A est
réalisé? Cette probabilité est appelée
probabilité conditionnelle de B sachant A et se note Que peut-on déduire sur la probabilité de
l'événement B sachant que l'événement A est
réalisé? Cette probabilité est appelée
probabilité conditionnelle de B sachant A et se note
P (B/A). Dans notre cas, on P (B/A)=k/n
Par définition on a : P(B/A)=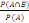 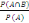
Conséquence
Deux événements A et B sont dits
indépendants si P(A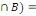 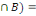 P(A).P(B) ou encore si P(B/A)=P(B) (l'information sur la
réalisation de A n'apporte rien à l'événement B) et
P(A/B)=P(A) P(A).P(B) ou encore si P(B/A)=P(B) (l'information sur la
réalisation de A n'apporte rien à l'événement B) et
P(A/B)=P(A)
III.2.1.5 Notion d'indépendance stochastique ou
indépendance en probabilité des
événements
Soient A, A1, A2, .........,
Ai, ........., An des événements dans ?
a) ces n événements sont indépendants en
probabilité 2 à 2(ou stochastiquement indépendants 2
à 2) si et seulement si 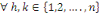 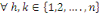 l'ensemble des indices, avec h l'ensemble des indices, avec h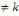 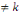 : IP (Ah Ak ) =
IP(Ah).IP(Ak) : IP (Ah Ak ) =
IP(Ah).IP(Ak)
b) ces événements sont indépendants en
probabilité (ou stochastiquement indépendants) k à k,
avec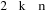 , si et seulement combinaison de k éléments
(i1, i2, .......ik) de l'ensemble , si et seulement combinaison de k éléments
(i1, i2, .......ik) de l'ensemble 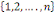 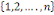 on a : on a : 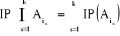
c) ces n événements sont indépendants en
probabilité dans leurs ensembles (ou stochastiquement
indépendants dans leur ensemble ou mutuellement indépendants) ssi
k   combinaisons combinaisons 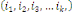 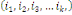 des éléments des éléments 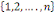 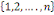
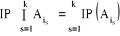
III.2.1.6. Théorèmes fondamentaux du
calcul des Probabilités
III.2.1.6.1 Théorème de la
multiplication des probabilités
Hypothèse :
- Soient des événements A1,
A2, ..., An en nombre fini
- Supposons que les événements A1,
A2, ..., An-1 ne sont pas incompatibles.
Thèse :
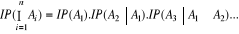 = = 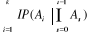 ; où A0 = Ù. ; où A0 = Ù.
III.2.1.6.2 Théorème (ou
Formule) des probabilités totales
Hypothèse :
Soient les événements A1,
A2, ..., An formant un système complet
(c'est-à-dire n événement totalement exclusifs),
c'est-à-dire :
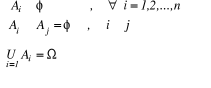
Supposons qu'un autre événement B ne puisse se
réaliser qu'en combinaison avec l'un des événements
Ai, (i = 1, 2, ..., n) c'est-à-dire
B =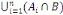 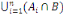
Thèse : IP (B) =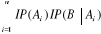
III.2.1.7 Théorème (ou formule) de
Bayes
Hypothèse : Mêmes hypothèses que pour
le théorème des probabilités totales.
Thèse :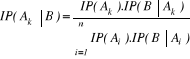 où k ? {1, 2, ..., n} et B ?Ø. où k ? {1, 2, ..., n} et B ?Ø.
Remarque :
v Le théorème de Bayes s'appelle encore
théorèmes des probabilités de causes.
v Le théorème de Bayes s'appelle encore
théorèmes des probabilités à posteriori, en effet
les IP (Ai), (i = 1, 2, ......, n) sont des probabilités
à priori ou données à l'avance tandis que les
IP (Ai B), (i = 1, 2, ......, n) se calculent
après que l'événement B se soit produit.
III.2.1.8 VARIABLES ALEATOIRES ET LOIS DE
PROBABILITE
III.2.1.8.1 La tribu Borélienne sur IR
notée â
â est une famille d'éléments de IR tel
que :
Ø Axiome: IR ? â ;
Ø Axiome: Si B ? â alors 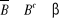 : stabilité par rapport à la
complémentarité ; : stabilité par rapport à la
complémentarité ;
Ø Axiome: Si Bi ? â, (i = 1, 2, ...),
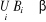 : stabilité par rapport à l'union
dénombrable. : stabilité par rapport à l'union
dénombrable.
Les éléments de â sont appelés des
Boréliens et notés B1, B2
,...,Bi ,...
Définition Un
Borélien est tout ensemble numérique
Exemples : Un ensemble dénombrable des
Réels. Ainsi tout intervalle de IR est un Borélien, mais la
réciproque n'est pas vraie : tout Borélien n'est pas un
intervalle de IR.
III.2.1.8.2 Définitions de Variable
Aléatoire
Nous noterons les Variables Aléatoires les
dernières lettres majuscules de l'alphabet :
Y, Z, U,..., Xj (j=1,2,...)
Soient (Ù, ?, IP), IR l'ensemble des Réels et
la classe de tous les intervalles de IR ;
Définition 1: On appelle
Variable Aléatoire X sur l'espace probabilisé (Ù, ?, IP),
l'application X :(Ù, ?, IP) ? IR vérifiant la
condition : intervalle I ? ,
X-1(I) ? ? ou encore X-1() ?.
Remarque :
1°) X-1(I) = {ù ? Ù tel que X
(ù) ? I}.
2°) En réalité une V.A.X est une
application de Ù dans IR, X : Ù? IR tel que I?,  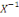 (I) ??. (I) ??.
Définition 2 :
On appelle Variable Aléatoire X une application
numérique
X :(Ù, ?, IP) ? IR vérifiant la condition B
?â, X-1(B) ? ? ou encore X-1(â) ?
Remarque :
1. X-1(B) = {ù ? Ù tel que X
(ù) ? B}.
2. (IR, â) est un espace mesurable ; en partant de
X et de la mesure de IP au sens de Kolmogorov on va définir une autre
mesure de IP qui sera notée IPX IP o X-1, cette
mesure sera appelée distribution de probabilité de la V.A.X.
Cas particuliers de variable
aléatoire
Soit X une variable aléatoire définie sur
(Ù, ?, IP) ; on appelle X (Ù) domaine de variation de X sur
Ù ensemble de toutes les valeurs que prend X sur Ùl'espace-
image de la V.A.X sur Ù.
Il y a deux classes de variable aléatoire :
1. Variable Aléatoire Discrète ou Variable
Aléatoire Discontinue (V.A.D.) : lorsque X (Ù) est au plus
dénombrable, c'est-à-dire lorsque 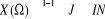 ; ;
2. Variable Aléatoire Continue (V.A.C.) lorsque X
(Ù) n'est pas dénombrable, c'est-à-dire lorsque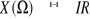 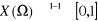
III.2.1.8.3 Lois de Probabilité
univariée
Nous distinguons deux lois de probabilité
univarieés relatives à une variable aléatoire X sur
un espace probabilisé (Ù, ?, IP). Il s'agit de IPX
appelée distribution de probabilité de la variable
aléatoire x et de FX appelée fonction de
répartition de la variable aléatoire x
Remarque :
Ø IPX est définie sur â
c'est-à-dire IPX est une fonction des ensembles
numériques (les Boréliens).
Ø FX est définie sur IR
c'est-à-dire FX est une fonction des points de IR.
III.2.1.9 VECTEURS ALEATOIRES ET LOIS DE PROBABILITE
MULTIVARIEES
III.2.1.9.1 Vecteur Aléatoire
Définition : On appelle
Vecteur Aléatoire à n composantes, le
n - uple des V.A : X= (X1, X2,
..., Xn).
Exemples
(1) Z = (X, Y) ; où X et Y sont des V.A., est un
couple de V.A. ; donc Z est un Vecteur Aléatoire à 2
composantes.
(2) X = (X1, X2) ; où
X1 mesure la taille et X2 le poids des étudiants
de l'UPN
X1(Ù) = { x11,
x12, ..., x1n} ; X2(Ù) = {
x21, x22, ..., x2n}
Où n = #Ù = nombre total
d'étudiants de l'UNIKIN.
Cas particuliers des vecteurs
aléatoires
(1) Vecteur Aléatoire Discret (ou Vecteur
Aléatoire Discontinu) :
X= (X1, X2, ..., Xn) est un
Vecteur Aléatoire discret ssi ses composantes X1,
X2, ..., Xn sont des V.A.D. définies sur
même (Ù, ?, IP).
Dès lors, les lois de probabilité
(IPX et FX) d'un Vect. al. Discret X= (X1,
X2, ..., Xn) sont des lois discrètes (ou
discontinues).
(2) Vecteur Aléatoire Continu :
Le Vecteur Aléatoire X= (X1, X2,
..., Xn) est Continu si et seulement ses composantes X1,
X2, ..., Xn sont des V.A.C. définies sur
même (Ù, ?, IP).
III.2.1.9.2 lois de probabilité
usuelles
Il est toujours possible d'associer à une variable
aléatoire une probabilité et définir ainsi une loi
de probabilité. Lorsque le nombre d'épreuves augmente
indéfiniment, les fréquences observées
pour le phénomène étudié tendent
vers les probabilités et les distributions observées
vers les distributions de probabilité ou loi de probabilité.
Identifier la loi de probabilité suivie par une variable
aléatoire donnée est essentiel car cela conditionne le choix des
méthodes employées pour répondre. Nous pouvons distinguer
deux catégories de lois particulières :
Ø Lois discrètes : Par définition,
les variables aléatoires discrètes prennent des
valeurs entières discontinues sur un intervalle donné. Ce sont
généralement le résultat de dénombrement.
Ø Lois continues : Par définition, les
variables aléatoires continues prennent des valeurs
continues sur un intervalle donné.
III.2.1.9.2.1 Loi normale
1. Définition : Une variable
aléatoire continue sera distribuée selon la loi normale de
moyenne m et d'écart type ó si sa fonction de fréquence
(ou densité de probabilité) fX est définie
par :
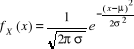 , x ? IR. , x ? IR.
Remarque :
1°) On vérifie par calcul direct que fX
est une fonction de fréquence :
fX (x) = 0 x ? IR et 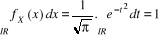 , par changement de variable d'intégration. , par changement de variable d'intégration.
2°) On vérifie par calcul direct :
v La moyenne est définie par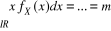 ; le premier paramètre de la loi normale N(m, ó) ; ; le premier paramètre de la loi normale N(m, ó) ;
v La variance est définie par 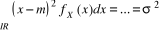 ; le carré du second paramètre de la loi normale
N(m, ó) ; ; le carré du second paramètre de la loi normale
N(m, ó) ;
3°) Pour toute variable aléatoire X de moyenne m
et d'écart type ó fini, la variable aléatoire
définie par 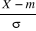 s'appelle variable aléatoire réduite ou variable
aléatoire centrée réduite correspondant à X ;
on a aussi : IE( s'appelle variable aléatoire réduite ou variable
aléatoire centrée réduite correspondant à X ;
on a aussi : IE(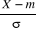 ) = 0 ; Var ( ) = 0 ; Var (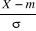 ) = 1 ; c'est-à-dire toute variable aléatoire
réduite a pour moyenne 0 et pour écart type 1. ) = 1 ; c'est-à-dire toute variable aléatoire
réduite a pour moyenne 0 et pour écart type 1.
4°) Si X est une V.A. N(m, ó), alors la variable
aléatoire Z = 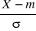 est donc une V.A. N(0 ; 1). est donc une V.A. N(0 ; 1).
| 


