Section 2 : Les
méthodes d'estimation.
Cette section présente les
différentes méthodes économétriques
utilisées dans l'estimation d'un modèle en panel statique. Pour
ce faire, nous allons commencer par tester l'homogénéité
de notre échantillon, c'est à dire de vérifier s'il y a ou
non des effets individuels spécifiques. En second lieu, nous utiliserons
le test d'Hausman (1978) pour savoir si notre modèle est
spécifié à partir d'un panel avec effets fixes ou effets
aléatoires.
1) Modèle à
effets fixes
Le modèle à effets fixes présume que les
relations entre la variable dépendante et les variables explicatives
sont similaires pour tous les individus. Si l'on considère
N individus, observés sur
Ti périodes de temps et
K variables explicatives, le modèle s'écrit
alors :
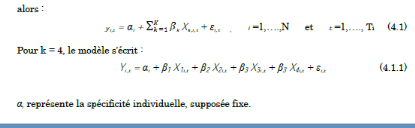
Pour k= 4, le modèle s'écrit ;
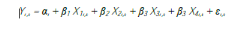
?i ; Représente la spécification
individuelle
2) Modèle à
effets aléatoires
On peut aussi modéliser les effets individuels
spécifiques d'une manière aléatoire variant autour d'une
moyenne.
L'existence des effets spécifiques conduit à une
auto-corrélation temporelle des erreurs pour le même individu mais
pas entre les individus.
Afin de choisir entre la modélisation à effet
fixe ou aléatoire, on va passer par le test d'Hausman.
3) Test
d'homogénéité de Fisher
Le test d'homogénéité de Fisher permet de
tester les effets spécifiques dans notre l'échantillon.
Nous rappelons les hypothèses de ce test :
H0 : ái = á
et âi = modèle homogène
H1: ái ? á et âi
=â+ modèle hétérogène
4) Test d'Hausman
Le test d'Hausman (1978) est un test de spécification
qui permet de déterminer si les coefficients des deux estimations (fixes
ou aléatoire) sont statiquement différents.
Soit ;
- H0 : E (ui / X) ? 0
H0 indique que le modèle peut être spé
- cifié avec effets individuels fixes
- H1 : E (ui / X) = 0
H1 indique que le modèle est considéré avec
effets individuels aléatoires.
La statistique du test est la suivante :
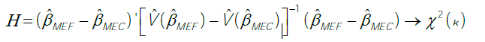
| 

