Introduction
En 1983, Morlet en travaillant sur l'analyse de signaux
sismiques s'est retrouvé confronté à la Rigidité
imposée par la taille fixe de la fenêtre de la transformée
de Fourier à fenêtre glissante. Il décide alors d'utiliser
une fenêtre de taille dilatée ou contractée selon les
besoins. L'idée des ondelettes était née.
Rapport Rédigé et présenté
par SIMO TEGUEU et EMBOLO AURELIEN Page 19
CHAPITRE II : DE L'ANALYSE DE FOURRIER A L'ANALYSE PAR
ONDELETTES
Principe
L'idée de l'ondelette est de pouvoir faire varier les
largeurs en temps et en fréquences d'une fonction tout en la translatant
le long du signal comme dans la transformée de Fourier
fenêtrée. Pour rappel, le but de l'analyse à fenêtres
est de pouvoir analyser localement les propriétés spectrales d'un
signal. La transformée en ondelette d'une fonction f en un
point (t ;ù) du plan temps-fréquences ne dépend donc que
des valeurs de f(t) et f(ù) dans le
rectangle de Heisenberg centré en (t ;ù). L'avantage de
faire varier ces largeurs devient alors évident : on minimise le nombre
de translations en temps et en fréquences de la fenêtre en
optimisant la largeur de celle-ci. Ainsi dans les basses fréquences, une
grande largeur en fréquences n'est pas nécessaire, on peut donc
utiliser des rectangles plus larges en temps. Aux hautes fréquences, on
va utiliser des rectangles plus larges en fréquences et plus
localisés en temps. On peut voir cela comme une adaptation de
l'ondelette à l'échelle qu'on lui impose : plus la fenêtre
est petite dans le temps, plus l'ondelette va être compressée et
osciller rapidement. Le contraire se produira lorsque la fenêtre est
dilatée. Ainsi, les petites et grandes fenêtres enregistreront
respectivement les variations rapides et moyennes du signal.
La transformée
Une ondelette mère 1)b est une fonction de
base que l'on va translater et dilater pour recouvrir le plan
temps-fréquences et analyser le signal. L'ondelette doit être une
fonction de moyenne nulle ; en d'autres termes, ø doit être une
onde ! Ce qui s'écrit mathématiquement :
>
+8 1)b(t)dt = 0 ,8
C'est la condition d'amissibilité. Elle doit
vérifier aussi une autre condition celle de régularité qui
consiste à faire décroître la transformée en
ondelettes le plus rapidement possible à mesure que l'échelle
décroît.
CHAPITRE II : DE L'ANALYSE DE FOURRIER A L'ANALYSE PAR
ONDELETTES
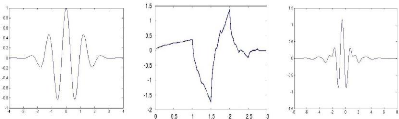
Figure 4 Quelques exemples d'ondelettes : Morlet, Daubechies
et Meyer
Il est à noter qu'il existe de nombreuses ondelettes.
Certaines ont des formules mathématiques explicites alors que d'autres
sont construites à partir de propriétés
mathématiques plus complexes. Chaque famille d'ondelettes
générée par une ondelette appelée ondelette
mère possède les qualités bien spécifiques, comme
par exemple :
> La symétrie : utile pour éviter le
déphasage,
> Le nombre de moments nuls : c'est-à-dire le
nombre d'oscillations ; utile pour la compression,
> La régularité : utile pour obtenir des
signaux reconstruits lisses et réguliers
Le logiciel MATLAB grâce à ses fonctions
wavenames et waveinfo présente une
variété d'ondelettes et leurs caractéristiques. Le tableau
ci-après présente quelques ondelettes les plus couramment
utilisées.
|
Haar
|
Daubechies
|
Meyer
|
Gaussian
|
|
Orthogonal
|
yes
|
yes
|
yes
|
no
|
|
Biorthogonal
|
yes
|
yes
|
yes
|
no
|
|
Compact Support
|
yes
|
yes
|
no
|
no
|
|
DWT
|
possible
|
possible
|
possible but without FWT FIR based approximation provides
FWT
|
no
|
|
CWT
|
possible
|
possible
|
Possible
|
possible
|
|
Support width
|
1
|
2N-1
|
infinite
|
infinite
|
|
Filters length
|
2
|
2N
|
|
|
|
Regularity
|
Not continuous
|
about 0.2 N for large N
|
indefinitely derivable
|
|
Rapport Rédigé et présenté par SIMO
TEGUEU et EMBOLO AURELIEN Page 20
| 


