Les fractals et leur géométrie

CHAPITRE 2

DIMENSION ET MESURES DE HAUSDORFF

Dans ce chapitre, nous etudions les mesures de Hausdorff et leurs proprietes pour introduire la dimension de Hausdorff qui s'appellera plus tard la dimension des fractals.

Section 2.1

Mesures de Hausdorff

Pour un sous-ensemble non vide U de l'espace euclidien Rⁿ de dimension n, on definit le diamètre de U, notediam(U), par : diam(U) := sup{|x - y| : x, y ? U} o`u | · | est la distance euclidienne usuelle.

Si un ensemble F est recouvert par une collection denombrable d'ouverts {Ui} de diamètre

00

au plus 8, c'est-`a-dire F ? Ui avec 0 < diam(Ui) 68pour tout i, on dit que {Ui} est un

i=1

8-recouvrement de F.

Soit F un sous-ensemble de Rⁿ et soit s un reel positif. Pour tout 8 > 0, on definit

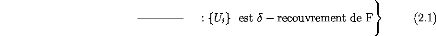
00

H;^s5(F) := inf {á(s) · E (diam(Ui)) s

vol^s(B_r)

i=1

2

o`u á(s) := _rs

_ðs/2

= (s ₂ +1) (voir [3, p. 327]) avec (t) =

+00_f

0

}: {Ui} est 8 - recouvrement de F (2.1)

e^-xx^t-1dx verifie

(1) = 1, (¹₂) = vð, (t + 1) = t(t)

et vol^s(B_r) signifie le volume de la boule de rayon r en dimension s.¹

1. Cette formule est pour s ? N, mais si l'on cherche a` d'efinir des dimensions s non enti`eres, il est naturel d'utiliser la màeme formule pour á(s).

D'efinition 2.1.1 Soient F ? Rⁿ, 0 -<, s < +8 et 0 < 8 < +8. On d'efinit la mesure de Hausdorff s-dimensionnelle H^s de F par

H^s(F) := lim ä--0

H^sä(F) = sup ä>0

H^sä(F) (2.2)

avec la convention H^s(F) = +8 pour s < 0.

Remarque 2.1.2

- Comme H^s_ä(F) est clairement une fonction decroissante de 8, l'existence de lim H^s_ä(F)

ä--0

est assuree, et cette limite est un supremum et peut àetre egal a` 0 ou a` +8.

- Cette mesure est appelee aussi la mesure de Hausdorff spherique (Falconer [8, 9]).

Les propositions suivantes donnent les premi`eres proprietes des mesures de Hausdorff.

Proposition 2.1.3 Pour tout s ?-. 0 et tout n ? N, la fonction F 7? H^s(F) est une mesure ext'erieure sur Rⁿ et d'efinit une mesure sur la tribu bor'elienne B(Rⁿ).

D'EMONSTRATION :

Il est clair que H^s(Ø) = 0 et que H^s est une fonction croissante d'ensembles. On verifie facilement que

H^sä(U kEN

Ak) ,<..E kEN

H^sä(Ak)

En passant a` la limite 8 ? 0 dans le terme de gauche, et en utilisant l'inegaliteH^s_ä ,<.. Hs dans le terme de droite, on trouve

H^s(U kEN

Ak) ,<..E kEN

H^s(Ak) (2.3)

La fonction H^s est donc sous-additive : c'est bien une mesure exterieure, definie sur l'ensemble de toutes les parties de Rⁿ.

Soit M la tribu des ensembles H^s-mesurables, au sens de l'enoncedu Theor`eme 1.2.2 ; on sait que H<sup>s</sup> definit une mesure sur M. Pour verifier que M contient toutes les parties boreliennes, on utilise le crit`ere de Caratheodory presenteau Theor`eme 1.2.5. Soient donc A et B deux parties de R<sup>n</sup> verifiant d(A, B) > 0, on cherche a` montrer que

H^s(A ? B) = H^s(A) + H^s(B). (2.4)

Pour tout 8 < d(A, B)/2, un ensemble de diam`etre 8 ne peut couper a` la fois A et B. Si l'on se
donne un recouvrement de A?B par des ensembles de diam`etre au plus 8, on pourra donc en

extraire des sous-recouvrements disjoints de A et B en considérant d'une part les ensembles qui coupent A, d'autre part ceux qui coupent B. On déduit que H^s_ä(A?B) = H^s_ä(A)+H^s_ä(B), et la conclusion en découle par passage a` la limite.

111

Proposition 2.1.4 Si F ? 118ⁿ et ë > 0, alors

H^s(ëF) = ë^sH^s(F) o`u ëF = {ëx : x ? F} (2.5)

D'EMONSTRATION :

Si {Ui} est un ä-recouvrement de F, alors {ëUi} est un ëä-recouvrement de ëF. D'o`u

H^sëä(ëF) 6 á(s)

(diam(2 ëUi) )s ës á(s) ^cE^° (diam(Ui))^s Hëä(ëF) 6 ë^sH^sä(F) ) 2 ) i=1 i=1

comme l'inégalitéest valable pour tout ä-recouvrement {Ui}, en faisant tendre ä ? 0, on obtient

H^s(ëF) = lim ä--0

H^sä(ëF) = lim ä--0

H^sëä(ëF) 6 ë^s lim ä--0

H^sä(F) = ë^sH^s(F).

En remplacant ë par 1/ë et F par ëF on obtient l'autre inégalité, d'o`u le résultat.

111

Un raisonnement similaire donne une estimation de la mesure de Hausdorff sur l'effet de transformations sur les ensembles.

Proposition 2.1.5 Soit F ? 118ⁿ et soit f : F ? 118^m une application lipschitzienne, i.e. |f(x) - f(y)| 6 c|x - y|, ?x,y ? F (2.6)
pour une constante c > 0. Alors, pour tout s > 0

H^s(f(F)) 6 c^sH^s(F) (2.7)

D'EMONSTRATION :

Si {Ui} est un ä-recouvrement de F, comme |f(F n Ui)| 6 c|F n Ui| 6 c|Ui|, on a que {f(F n Ui)} est un å-recouvrement de f(F), o`u å = cä.

Donc á(s) Ei

(diam(f(F n Ui)))s cs á(s) Ei 2 (diam(Ui))^s 2 . . , anis]. en prenant d'abord

(diam(Ui))^s

l'infinimum sur les 6-recouvrements, on a H^s_å(f (F)) < c^s · á(s) Ei 2 , ensuite,
comme l'in'egalit'e est vraie pour tout 8-recouvrement, en prenant l'infinimum sur ceux-ci, on

obtient H^s_å(f(F)) < c^sH^s_ä(F). Quand 8 ? 0 on a 6 ? 0 aussi, d'o`u le r'esultat. El

Si f est une isom'etrie, i.e. |f(x) - f(y)| = |x - y|, alors H^s(f(F)) = H^s(F). Donc, la mesure de Hausdorff est invariante par translation (i.e. H^s(F + z) = H^s(F) o`u F + z = {x + z : x ? F}).

Rappellons qu'une mesure ext'erieure est dite r'eguli`ere si, pour tout ensemble A, il existe un ensemble u^*-mesurable X tel que A ? X et u^*(A) = u^*(X).

Le lemme suivant est utile pour la suite. Voir Falconer[8, p. 4] pour la d'emonstration. Lemme 2.1.6 Si u* est une mesure exterieure r'eguli`ere et si {Ai}i est une suite croissante d'ensembles, alors

lim _k8u^*(Ai) = u^*(limAi). (2.8)

i--

i?8

Th'eor`eme 2.1.7 (R'egularit'e de la mesure de Hausdorff)

Soit s > 0 et soit A ? Illⁿ une partie quelconque. Alors

1. Il existe un ensemble Gä not'e G avec A ? G et tel que

H^s(G) = H^s(A) (2.9)

2. Si A est H^s-mesurable et H^s(A) < +8, alors il existe un ensemble F_ó not'e H avec H ? A et tel que

H^s(H) = H^s(A). (2.10)

D'EMONSTRATION :

1. Si H^s(A) = +8 alors Illⁿ est l'ensemble ouvert de Mesure (de Hausdorff) infinie. Supposons que H^s(A) < +8. Pour tout k, on a Hs1/k(A) < H^s(A) < +8, et on choisit {Ui,k}i un 2/k-recouvrement de A, ouverts, telle que

X8 i=1

~diam(Ui,k) ~s '31 s ( ) + < k'^A / k1 á(s) 2

On pose alors

[Ok := Ui,k, G := n Ok.

iEN k>1

Il est clair que G contient A, et d'autre part pour tout k on a

7-1^s2/k(G) 6

00 i=1

~diam(Ui,k) ~s '31 s ( A 6 1/k k') + k1 á(s) 2

Il s'ensuit que 7-1^s(G) 6 7-1^s(A), d'o`u la conclusion.

2. Soit A est 7-1^s-mesurable et 7-1^s(A) < +Do. Par la partie 1 du theor`eme on definit des

ouverts Ok avec A ?

00 k=1

00 Ok telle que 7-1s( n k=1

Ok \A) = 7-1s( n k=1

Ok)-7-1^s(A) = 0. Comme

00

tout ouvert de Rⁿ est un F_ó, on suppose que Ok = Fi_,k pour tout k, avec {Fi,k}k

i=1

suite de fermes croissante. Gràace au Lemme 2.1.6 ci-dessus

lim i-00

7-1^s(A n Fi,k) = 7-1^s(A n Ok) = 7-1^s(A).

Pour tout E > 0 et k > 1 on choisit ik tel que

7-1^s(A\Fik,k) < 2^-kE.

On pose F :=

00 k=1

Fik,k ; on a alors

00

7-1^s(F) > 7-1^s(A n F) > 7-1^s(A) - 7-1^s(A\Fik,k) > 7-1^s(A) - E.

k=1

Comme F ?

00 k=1

00 Ok, alors 7-1^s(F\A) 6 7-1s( n k=1

Ok\A) = 0. Par la partie 1, il existe un

ensemble G, intersection denombrable d'ouverts, de mesure nulle, tel que F\A ? G.
Alors F_å := F\G est contenu dans A, c'est une intersection denombrable de fermes, et

7-1^s(F_å) > 7-1^s(F) - 7-1^s(G) = 7-1^s(F) > 7-1^s(A) - E.

On conclut en posant H := _S00 F1/k.

k=1

111

Soit A ? Rⁿ de demi-diam`etre r. Il est clair que le volume de A est 'egal a` á(n)rⁿ si A est une boule, mais que peut-on dire dans le cas g'en'eral? On est tent'e de penser que A est inclus dans une boule de rayon r ou r + 6 avec 6 > 0 arbitrairement petit, mais ce n'est pas forc'ement le cas, comme le montre l'exemple d'un triangle de càot'e 1 dans R² et de diam`etre 1. Cependant, l'in'egalit'e isodiam'etrique ci-dessous assure que le volume d'un tel ensemble est inf'erieur ou 'egal a` celui d'une boule de màeme rayon.

Th'eor`eme 2.1.8 (In'egalit'e isodiam'etrique)

Soit A ? Rⁿ un ensemble Lebesgue-mesurable, et r son demi-diam`etre. Alors

volⁿ(A) 6 á(n)rⁿ. (2.11)

Lemme 2.1.9 'Etant donneun cube Q et 6 > 0, on peut ecrire

[ Q = j>1

Bj ? N (2.12)

o`u les Bj sont des boules fermees de rayon au plus 6, disjointes, et N est un ensemble Lebesgue-negligeable.

Th'eor`eme 2.1.10 (Propri'et'es des mesures de Hausdorff) X H⁰ est la mesure de comptage, i.e. H⁰(A) = E

1.

pEA

® H¹(A) = L¹(A), ?A ? R.

(c) H^s(A) = 0, ?A ? Rⁿ si s > n. T Hⁿ(A) = Lⁿ(A), ?A ? Rⁿ.

D'EMONSTRATION :

X Soit p ? Rⁿ. Pour tout 8 > 0, par d'efinition, on a H⁰({p}) = 1.

® Soient A ? R et 8 > 0. On va montrer que L¹(A) > H¹ä(A) et puis L¹(A) 6 H¹ä(A). On a

L¹(A) = inf {E(bi - ai) : A ? ]ai, bi[

i=1 i=1

00

{ 00

= inf E(b_i -- a_i) : A c U]ai, bi[, 0 < bi - ai 6 8

i=1 i=1

> H¹_ä(A)

Pour l'autre in'egalit'e, supposons A ? U iEN

Ui, ai:= inf Ui et bi := sup Ui. On obtient

diam(Ui) = bi - ai et donc

00 00

H¹ä (A) = infá(1) Vbi - 2 ai : A ? U[ai, bi], 0 < bi - ai 6 ä {

L--^,

i=1 i=1

00 00

( _X [

i=1 i=1

= inf (bi - ai) : A ? [ai, bi], 0 < bi - ai 6 ä

Soit å > 0 et supposons que {Ui} soit un ä-recouvrement de A satisfaisant

00

]ai, bi[

i=1

00

_P
i=1

et

(bi-ai) < H¹ä(A)+å. Soient ai := ai- 2i^å+1 , et bi := bi+ å

2i+1 . Alors, on a A ?

L^1(A) 6

00 i=1

(bi - ai) 6

00 i=1

(bi - ai) +

00 i=1

2i < H1 å ä(A) + 2å

. Pour

m m

(c) On va recouvrir le cube unit'e n-dimensionnelle Q = [0, 1]ⁿ ? Rⁿ par mⁿ petits cubes Qm,k(1 6 k 1 mⁿ) avec des cotes de longueur (m ? N^* et de diamètre) vn

> 0, on choisit m tel que n m

< ä. Pour s > n, on a

H^s_ä(Q) 6 á(s)

X mⁿ_{~vn ~s}

2m

k=1

= á(s)

_vn s

2s_ms-n

Pour m ? +8, on obtient H^sä(Q) = 0 pour tout ä > 0. Alors H^s(Q) = 0. Comme Rn est un r'eunion d'enombrable des translations du cube unit'e, alors H^s(Rⁿ) = 0.

T Soit {Ui} un ä-recouvrement de A. Gràace a` l'in'egalit'e isodiam'etrique 2.1.8, on a

L^n(A) 6

00 i=1

vol^n(Ui) 6 á(n)

X00 ~diam(Ui) ~n 2 i=1

En passant a` l'infinimum, on voit que L<sup>n</sup>(A) 6 H<sup>n</sup><sub>ä</sub>(A), et donc L<sup>n</sup>(A) 6 H<sup>n</sup>(A). Il nous reste a` montrer l'in'egalit'e inverse.

Soit maintenant A un ensemble Lebesgue-mesurable, on choisit une famille {Ui} de cubes Qi recouvrant A telle que

00

i=1 volⁿ(Qi) 6 Lⁿ(A) + ä,

o`u 8 > 0 est arbitrairement petit. Pour de tels cubes, on peut trouver une constante c_n, dépendant uniquement de n, telle que

á(n)r(Qi)ⁿ = c_nvolⁿ(Qi)

On déduit que Hⁿ 6 c_nvolⁿ.

Pour chaque Qi on introduit une famille de boules _(Bi,j)j>1 et un ensemble négligeable Ni vérifiant les conclusions du Lemme 2.1.9; en particulier, Hⁿ(Ni) 6 c_n · 0 = 0. On a donc

H^n(A) 6

X8 i=1

H^n(Qi) =

X8 i=1

(E j>1

H^n(Bi,j) + H^n(Ni))

_X8

i=1

_X8

i=1

_X
j>1

Bi_,j) =

_E8

6

i=1

volⁿ(U

j>1

volⁿ(Bi_,j) =

volⁿ(Qi) 6 Lⁿ(A) + 8

111

Lemme 2.1.11 Soit A ? Illⁿ et supposons que 0 6 s < t < +8 et 8 > 0. Alors :

H^sä(A) > 8^s-tH^tä(A). (2.13)

D'EMONSTRATION :

Soit {Ui} un 8-recouvrement de A. Comme diam(Ui)^s = diam(Ui)^s-^t · diam(Ui)^t et diam(Ui)^s-^t > 8^s-^t, alors H^sä(A) > 8^s-^tH^tä(A).

111

Selon le Lemme 2.1.11, on a le théor`eme suivant :

Th'eor`eme 2.1.12

Soit A ? Rⁿ et supposons que 0 6 s < t < +8. Alors :

1. H^s(A) < +8 = H^t(A) = 0.

2. H^t(A) > 0 = H^s(A) = +8.

06 On peut le montrer facilement si nous utilisons (2.13)

D'EMONSTRATION :

1. Soit ä > 0 et supposons que {Ui}i?N satisfait diam(Ui) 6 ä et

á(s)
·

E8 ( ₂ )diam(Ui))s

6 7-1^sä

(A) + 1 6 7-1^s(A) + 1

i=1

On obtient	7-1^tä(A) 6 á(s) ·	X8 ~diam(Ui) ~t 2 i=1
á(t) = · á(s) · á(s)			X8 ~diam(Ui) ^~s ~diam(Ui) ~t-s 2 2 i=1

:((st)) (7-1^s(A) + 1)
· (2ä)t s
·

Pour ä ? 0, on obtient 7-1^t(A) = lim ä?0

7-1^tä(A) = 0.

2. l'assertion 2 est une consequence immediate de 1.

111

Section 2.2

Dimension de Hausdorff

D'apr`es le Theor`eme 2.1.12, la mesure s-dimensionnelle d'un ensemble vaut d'abord l'infini pour s petit, puis zero si s d'epasse un certain seuil, qui est precisemment la dimension de l'ensemble. Alors on a la definition suivante :

D'efinition 2.2.1 La dimension de Hausdorf f² d'un ensemble F est donn'ee par :

dimH(F) := sup{s : 7-1^s(F) = +8} = inf{s : 7-1^s(F) = 0}. (2.14)

On a donc

(

+8 si s < dimH(F)

7-1^s(F) = (2.15)

0 si s > dimH(F)

La dimension de Hausdorff satisfait les proprietes suivantes :

2. Que certains auteurs appellent «dimension de Hausdorff-Besicovitch».

H^s(F)

+8

0

		s

dimH(F)

FIGURE 2.1 --- Graphe de H^s(F) en fonction de s pour un ensemble F Th'eor`eme 2.2.2 (Propri'et'es de la dimension de Hausdorff)

1. A ? B = dimH(A) 6 dimH(B) ³. (Monotonie)

2. dimH (U Ai) = sup dimH(Ai). (Stabilit'e d'enombrable) 8

1. Si A ? 118ⁿ un ensemble d'enombrable, alors dimH(A) = 0.

2. Si A ? 118ⁿ un ensemble ouvert, alors dimH(A) = n.

3. dimH([0, 1]ⁿ) = n.

D'EMONSTRATION :

i=1

1. A ? B implique que H^s(A) 6 H^s(B). Donc on a dimH(A) = sup{s : H^s(A) = +8} 6 sup{s : H^s(B) = +8} = dimH(B).

8

2. Une cons'equence imm'ediate de la monotonie donne dimH ( U Ai I ?-. dimH(Ai), pour

i=1

tout 1 6 i 6 8. Alors

dimH		[ 8 i=1	Ai)> sup 16i68dimH(Ai).
Dans l'autre càot'e, si s > sup 16i68	dimH(Ai), alors H^s(Ai) = 0 pour tout 1 6 i 6 8. Donc

3. si A ? iRⁿ alors dimH(A) 6 n.

~

U Ai) = 0, qui donne i=1

dimH

[ 00 i=1

Ai)6 sup 16i600dimH(Ai).

00

3. Supposons A = {ai}. On a H⁰({ai}) = 1 et de plus H^s({ai}) = 0 pour tout s > 0

i=1

et i > 1. Ca implique que dimH({ai}) = 0 et par la partie 2 du theoreme, on a

dimH(A) = sup 16i600

dimH({ai}) = 0.

4. Comme A ? 118ⁿ, alors dimH(A) 6 n, et comme A contient une boule n-dimensionnelle (car tout ouvert de Illⁿ est un reunion denombrable de boules ouvertes n-dimensionnelles et bornees), alors dimH(A) > n. D'o`u l'egalite.

5. D'apres la partie 4 du Theoreme 2.1.10, on a Hⁿ([0, 1]ⁿ) = Lⁿ([0, 1]ⁿ) = 1 et par la partie 3 du màeme Theoreme, on a H^s([0, 1]ⁿ) = 0, ?s > n. Alors

dimH([0, 1]ⁿ) = inf{s : H^s([0, 1]ⁿ) = 0} = n.

El

Proposition 2.2.3 Soit F ? Illⁿ et soit f : F ? Ill^m une application lipschitzienne de constante c > 0. Alors, pour tout s > 0, on a

dimH(f(F)) 6 dimH(F) (2.16)

D'EMONSTRATION :

Si s > dimH(F), alors par la Proposition 2.1.5, on a H^s(f(F)) 6 c^sH^s(F) = 0 car H^s(F) = 0. Donc si H^s(f(F)) = 0, alors s > dimH(f(F)).

Ainsi, si s > 0 et s > dimH(F), alors s > dimH(f(F)). Donc dimH(f(F)) 6 dimH(F).

El

Corollaire 2.2.4 Soit f : F ? Ill^m une application bi-lipschitzienne, i.e.

? 0 < c1 6 c2, c1|x - y| 6 |f(x) - f(y)| 6 c2|x - y| (2.17)

Alors

dimH(f(F)) = dimH(F). (2.18)

Ce corollaire d'evoile une proprietefondamentale de la dimension de Hausdorff. «C'est l'invariance de la dimension de Hausdorff par des applications bi-lipschitziennes». Ainsi, deux ensembles de dimensions differentes ne peuvent avoir d'applications bi-lipschitziennes entre eux.

En general, la dimension donne certaines proprietes topologiques de l'ensemble. Par exemple, chaque ensemble de dimension plus petite que 1 est totalement discontinu comme le montre la proposition suivante.

Rappellons qu'un espace E est dit totalement discontinu si la composante connexe de chacun de ses points est l'ensemble reduit a ce point.

Proposition 2.2.5 Un ensemble F ? Rⁿ avec dimH(F) < 1 est totalement discontinu.

D'EMONSTRATION :

Soient x et y deux points distincts de F. Definissons une application f : Rⁿ ? [0, 1[ par f(z) = |z - x|. Comme f est contractante car |f(z) - f(w)| < |z - w|, on obtient par la Proposision 2.2.3 que dimH(f(F)) .<, dimH(F) < 1. Ainsi, f(F) est un sous-ensemble de R de mesure H¹ ou longueur nulle et a donc un complement dense. Choisissons r avec r ?/ f(F) et 0 < r < f(y), il s'ensuit que

F = {z ? F :|z - x| < r} ? {z ? F :|z - x| > r}

Donc F est la reunion de deux ouverts disjoints, l'un contenant x et l'autre y, donc x et y appartiennent a` deux composantes connexes differentes de F.

Th'eor`eme 2.2.6 (Dimension des graphes)

Soit f : Rⁿ ? R^m une fonction lipschitzienne et soit A une partie mesurable de Rⁿ. On note G(f, A) = {(x, f(x)) : x ? A} le graphe de f sur A. Alors

dimH(G(f, A)) = n si Lⁿ(A) > 0 (2.19)

Remarque 2.2.7

- De manière generale, la dimension de Hausdorff d'un graphe est superieure ou egale a` la dimension de l'espace de depart ; elle peut être strictement superieure pour des applications qui sont seulement Hàolderiennes (ou encore moins regulières) et pas Lipschitziennes.

Section 2.3

Calculs des dimensions

4. L1(C) = L^1(

T00 k=1

Ck) = lim k-+oo

L1 (Ck) = kli>m00 (23) = 0.

Nous allons a` present calculer les dimensions de Hausdorff de quelques ensembles simples et bien connus. Commençons par l'exemple utilisepar Hausdorff lui-même pour illustrer sa notion de dimension.

Exemple 2.3.1 L'ensemble triadique de Cantor :

L'ensemble triadique de Cantor est d'efinit comme la limite des ensembles ferm'es Ck, o`u C0 = [a, b] (prenant [a, b] = [0, 1]) et Ck est obtenu a` partir de _{Ck_1} en supprimant le tiers (ouvert) central de chacune des composantes connexes de _{Ck_1.} L'ensemble r'esultant est clairement de mesure de Lebesgue nulle ⁴, on peut se demander quelle est sa dimension.

FIGURE 2.2 - Premi`eres etapes de la construction de l'ensemble triadique de Cantor

Th'eor`eme 2.3.2

log 3.

Soit C l'ensemble triadique de Cantor. Alors dimHC ₌log 2 La dimension de Hausdorff est dejàplus difficile a` calculer. Par ailleurs, on peut faire un calcul heuristique simple en tirant parti de la construction auto-similaire de l'ensemble C et la proposition de changement d'echelle 2.1.4.

CALCUL HEURISTIQUE :

L'ensemble de Cantor se divise en sa partie gauche C_g = C n [0, 3 1] et sa partie droite Cd = Cn[²₃,1], toutes deux egales a` l'ensemble de Cantor multiplie par un facteur ₃¹. Comme C est reunion disjointe de ces deux parties, C = C_g ? Cd. On a pour tout s > 0

2

H⁸(C) = H⁸(C_g) + H⁸(Cd) = ₍₃ 1)8 H8 (C) + (31)8 H8 (C) = ₃₈H⁸ (C)

ce qui impose 3^s = 2, i.e. s =

log 2

log 3.

On peut le faire par un calcul rigoureux mais avec moins des conditions.

CALCUL :

Notons Ck la reunion des intervalles de longueur 3-^k, appeles intervalles fondamentaux,

lors de la ^k`eme etape dans la construction de C = _T8 Ck. Soit {Ui} le recouvrement de C

k=0

composede 2^k intervalles de longueur 3-^k. Comme C est compact (voir [4]), on peut toujours supposer que les Ui forment une collection finie de sous-intervalles fermes de [0, 1]. Ainsi, en supposant que ce recouvrement est celui pour lequel l'infinimum est atteint, on trouve :

H^s(C) = lim k?8

1-k s k (C) = lim á(s) · 2^k · (- 2 ) . ? k8

k

Apr`es rearrangement des termes, H^s(C) = á(s) lim . Or, cette limite tend vers 0

2s k?k8 ( 2 3s

2 8 pour verge 1, et elle 32s

lorsque ₃ 1lle di a l'infini > 1. Autrement dit, elle se situe entre 0

et +8 lorsque 2

= 1, c'est-`a-dire pour s = log 2 Donc, la dimension de Hausdorff de

3s log 3

log 3.

Remarque 2.3.3

- La methode de calcul «heuristique» utilisedans le Theor`eme 2.3.2 donne la vraie reponse pour la dimension de plusieurs ensembles auto-similaire.

l'ensemble triadique de Cantor est log 2

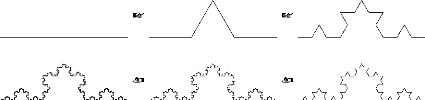
Exemple 2.3.4 La courbe de von Koch :

On obtient la courbe de Koch par it'erations a` partir du segment [0, 1] en remplacant le tiers central par un triangle 'equilat'eral de cot'e le tiers qu'on enl`eve, puis en recommencant cette op'eration a` l'infini sur chaque segment de la figure obtenue.

Th'eor`eme 2.3.5 Soit K la courbe de Koch. Alors dimHK = log 4

log 3.

CALCUL HEURISTIQUE :

La courbe de von Koch se divise en quatre partie egaux a` la courbe de von Koch multiplie₁ par un facteur ₃. On a pour tout s > 0

H^s(K) = 4 · H^s(¹₃K) = 4 Hs(K)

3s

11 Z'

FIGURE 2.3 - Premi`eres etapes de la construction de la courbe de von Koch ce qui impose 3^s = 4, i.e. s = log 4

log 3.

CALCUL :

Soit {UiI le recouvrement de K composede 4^k intervalles de longueur 3-^k. Ainsi, en supposant que ce recouvrement est celui pour lequel l'infinimum est atteint, on trouve :

7-1^s(K) = lim k?8

7-1^s3-k (K) = lim á(s) · 4k (32k) s = lim á(s) ( 38) 4 koo k--oo 2^8 ?

4 4

Or, cette limite tend vers 0 lorsque < 1, et elle diverge a l'infini pour > 1. Autrement

3s 3s

dit, elle se situe entre 0 et +Do lorsque 4 = 1, c'est-`a-dire pour s = log 4. Donc, la dimension

3s log 3

log 3^.

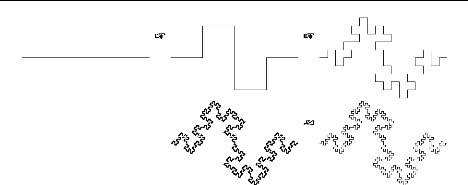
Exemple 2.3.6 La courbe de Koch quadratique (type 1) :

On obtient La courbe de Koch quadratique (type 1) par it'erations a` partir du segment [0, 1] en remplacant le tiers central par trois cot'es d'un carr'e, puis en recommencant cette op'eration a` l'infini sur chaque segment de la figure obtenue.

de Hausdorff de la courbe de von Koch est log 4

Th'eor`eme 2.3.7

Soit K1 la courbe de Koch quadratique de type 1. Alors dimHK1 = log 5

log 3.

CALCUL HEURISTIQUE :

La courbe de Koch quadratique de type 1 se divise en cinq parties egales a` la courbe de 1

Koch quadratique multipliepar un facteur ₃. On a pour tout s > 0

5

7-1^s(K1) = 5
· 7-1^s(₃K1) = _3s 7-1^s(K1

11 Z'

FIGURE 2.4 - Premi`eres 'etapes de la construction de la courbe de Koch quadratique 1

ce qui impose 3^s = 5, i.e. s =	log 5
	log 3.

CALCUL :

Soit {UiI le recouvrement de K1 compos'e de 5^k intervalles de longueur 3-^k. Ainsi, en supposant que ce recouvrement est celui pour lequel l'infinimum est atteint, on trouve :

7-1^s(K1) = lim k?8

k 7-1^s-k (K1) = lim á(s) · 5k (32k )s = li k-- 28 m á(s) ( 38) 5 k?8 oo

5 8 pour < 35s

Or, cette limite tend vers 0 lorsque ₃ 1 et elle diverge a l'infini > 1. Autrement

dit, 5

elle se situe entre 0 et +cc lorsque = 1, c'est-`a-dire pour s = log 5 Donc, la dimension

3s log 3

log 3^.

Exemple 2.3.8 La courbe de Koch quadratique (type 2) :

On obtient la courbe de Koch quadratique (type 2) par iterations a` partir du segment [0, 1]
en le partageant sur huit segments de màeme longueur et en joignant les points suivants

de Hausdorff de la courbe de Koch quadratique de type 1 est log 5

consecutivement :

p0=(0,0)	p1=(0.25,0)	p2=(0.25,0.25)
p3=(0.5,0.25)	p4=(0.5,0)	p5=(0.5,-0.25)
p6=(0.75,-0.25)	p7=(0.75,0)	p8=(1,0),

puis en recommencant cette operation a` l'infini sur chaque segment de la figure obtenue.

11 Z'

FiGuRE 2.5 - Premi`eres etapes de la construction de la courbe de Koch quadratique 2 Th'eor`eme 2.3.9

log 4 2

Soit K2 la courbe de Koch de type 2. Alors dimHK2 ₌log 8 3 CALCuL HEuRisTiQuE :

La courbe de Koch quadratique de type 2 se divise en huit partie egales a` la courbe de

1

Koch quadratique multipliepar un facteur ₄. Pour tout s > 0

7-1^s(K2) log 8	= =	8 · 3 2	1 7-1^s(4	=4s^87-1^s(K1)
impose 4^s 8, i.e. ce qui = s = log 4

CALCuL :

Soit {UiI le recouvrement de K1 composede 8^k intervalles de longueur 4-^k. Ainsi, en supposant que ce recouvrement est celui pour lequel l'infinimum est atteint, on trouve :

7-1^s(K2) = lim 7-1^s4-k(K2) = lim k?8 k?8

8k ( 4-k s ..m á(s) ( 8 )k á(s) · = 11 2 k?8 2^s 4^s)

8 8

4s

Or, cette limite tend vers 0 lorsque 4s < 1 et elle diverge a` l'infini pour > 1. Autrement

8

dit, elle se situe entre 0 et +Do lorsque = 1, c'est-`a-dire pour s = log 8. Donc, la dimension

4s log 4

de Hausdorff de la courbe de Koch quadratique de type 2 est 3.

2

Exemple 2.3.10 Le flocon de von Koch :

Le flocon de Koch s'obtient de la même facon que la courbe de von Koch 2.3.4, en partant d'un triangle equilateral au lieu d'un segment de droite, et en effectuant les modifications en orientant les triangles vers l'exterieur.

FIGURE 2.6 - Premi`eres étapes de la construction d'un flocon de von Koch

Th'eor`eme 2.3.11

Soit FK un flocon de von Koch. Alors dimHF K ₌log 4

log 3.

CALCUL :

Comme le flocon de Koch est une réunion finie des courbes de von Koch FK =

3

U Ki et

i=1

par la propriété2 du Théor`eme 2.2.2 on a :

3

log 4

dimH(FK) = dimH U Ki = sup dimH(Ki) = dimH(K) = log 3

15i53 i=1

Exemple 2.3.12 Le triangle de Sierpinski :

On obtient le triangle de Sierpinski par iterations a` partir d'un triangle equilateral duquel on enl`eve le triangle central, i.e. celui dont les sommets sont les milieux des cotes du triangle de depart, et on recommence cette operation a` l'infini sur chaque triangle restant.

FIGURE 2.7 - Premi`eres étapes de la construction d'un triangle de Sierpinski

Th'eor`eme 2.3.13

log 2.

Soit S le triangle de Sierpinski. Alors dimHS ₌log 3

CALCUL :

On voit que le recouvrement optimal utilise des boules de diam`etre 8 = 2 · ^v3. Notons

2k

que 8 tend vers 0 lorsque k tend vers l'infini. Dans chaque cas, on utilise 3^k boules. Ainsi, en

supposant que ce recouvrement est celui pour lequel l'infinimum est atteint, on trouve

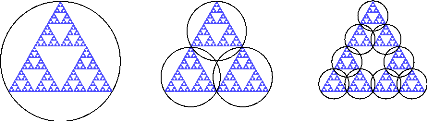
FIGURE 2.8 - Recouvrements d'un triangle de Sierpinski

H^s(S) = lim ä-.0

H^sä(S) = lim k-.00

s v3 á(s) · 3k 2k 3 = V3 · a(s) ( 2s)

Or, cette limite tend vers 0 lorsque 3 3 < 1 et elle diverge a` l'infini pour > 1. Autrement

2s 2s

dit, elle se situe entre 0 et +8 lorsque 3 = 1, c'est-`a-dire pour s = log 3 Donc, la dimension

2s log 2

log 2.

Exemple 2.3.14 Le tapis de Sierpinski :

L'id'ee de l'ensemble de Cantor est de couper un segment en parties 'egales, d'enlever une de ces parties, et de recommencer. C'est cette id'ee qui pr'eside aux tapis de Sierpinski que nous allons examiner.

de Hausdorff du triangle de Sieprinski est log 3

Th'eor`eme 2.3.15

Soit S le tapis de Sierpinski. Alors dimHS = log 8log 3.

FIGURE 2.9 - Premieres étapes de la construction d'un tapis de Sierpinski

Voir l'exemple prochain pour le calcul concernant cet exemple.

Exemple 2.3.16 L'éponge de Menger :

On obtient l'éponge de Menger par itérations a` partir d'un cube qu'on découpe en 27 cubes de cotés le tiers du premier, puis on enlêve le petit cube central et les 6 cubes ayant une face commune avec lui, on recommence cette opération a` l'infini sur chaque cube restant. Avec d'autre maniêre si chaque face de l'éponge de Menger est un tapis de Sierpinski.

Théorème 2.3.17

log 20

Soit M l'éponge de Menger. Alors dimHM =

FIGURE 2.10 - Premieres étapes de la construction de l'éponge de Menger

log 3 .

D'une maniere générale, McMullen, est dans [22], démontre que la dimension de Hausdorff d'une carpette de Sierpinski généraliséR qui définie par

( 00X ! }

\' 00

xk yk

R = nk , : (xk, yk) ? A (2.20)

_mk

k=1 k=1

o`u A c {(a, b) : 0 6 a < n, 0 6 b < m, n m} telle que dimH(R) = logm

m-1 P j=0

) tlogn m o`u j

log r

tj est le nombre de i tels que (i, j) ? A. Si n = m, on a dimH(R) = avec r = |A|.

log n

11 Z'

Pour l'exemple 2.3.14, on a n = m = 3 et r = 8 et pour l'exemple 2.3.16 on prend n = m = 3 et r = 20.

Exemple 2.3.18 La courbe de Peano :

On obtient la courbe de Peano par it'erations a` partir du segment [0,1] en le partageant sur neuf segments de màeme longueur et en joignant les points suivants cons'ecutivement :

p0 = (0,0) p1 = (¹₃,0) p2 = (¹₃,¹₃)

p3 = (²₃,¹₃) p4 = (²₃, 0) p5 _=(13, 0)

p6 = (3¹, 3) p7 ₌(2_{3, 3})

p8 = (²₃, 0)

p9 = (1, 0).

puis en recommencant cette op'eration a` l'infini sur chaque segment de la figure obtenue.

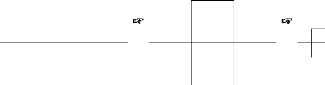
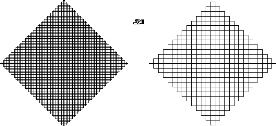
FIGURE 2.11 - Premi`eres étapes de la construction de la courbe de Peano

Th'eor`eme 2.3.19 log 9 Soit P la courbe de Peano. Alors dimHP^=log 3

= 2.

CALCUL :

De même facons, soit {Ui} le recouvrement de P compos'e de 9^k intervalles de longueur 3-^k. Ainsi, en supposant que ce recouvrement est celui pour lequel l'infinimum est atteint, on trouve :

7-1^s(P) = lim ä?0

7-1^sä(P) = lim k?8

^k á(s) . 9k (3 k) = lim á(s) ( 9 ) . 2 k?8 2s 3s

Cette limite se situe entre 0 et +oo lorsque 9 = 1, c'est-h-dire pour s = log 9. Donc, la

3s log 3

dimension de Hausdorff de la courbe de Peano est 2.