Efficience des marchés et Méthodes de Monte Carlo : Peut-on réaliser des profits anormaux au moyen de l'Analyse Technique ?

C. Bootstrap

Afin de vérifier la significativité des résultats semblant remettre en cause l'efficience faible des marchés, nous nous sommes attachés à créer un modèle de Bootstraping qui pourra sans doute nous apporter des éléments complémentaires de réponse. En effet, le bootstraping consiste en une méthode informatique de rééchantillonage, sans données supplémentaires que celles de l'échantillon de départ. Dans cette étude, le modèle stochastique utilisé pour réaliser ce bootstrap diffère de celui de Brock et al. (1992), qui en en ont choisi plusieurs, soit plus simples, comme celui de la marche aléatoire, ou plus élaborés, comme les modèles GARCH ou ARCH, dont l'inventeur, Robert Engel, reçu un prix Nobel en 2003. La méthodologie abordée ici différera également de celle de Brock et al. (1992), et tendra davantage vers celle

adoptée par Sullivan, Timmermann, et White (1999). Effet, nous analyserons les résultats ainsi que leur significativité par rapport aux critères du ratio de Sharpe.

1. Le choix du modèle

Notre étude empirique sur l'historique des cours du CAC40, nous a conduit à la très faible auto-corrélation des log-rentabilités. Nous choisirons donc un modèle de formation des prix S(k), cohérent avec la non-corrélation des rentabilités logarithmiques R = lnS(k+1) - lnS(k). En outre, cette représentation est cohérente avec le marché, car les prix ne peuvent être négatifs, (le domaine de définition de la fonction ln x est ]0,+oo[ ) et est cohérente avec l'efficience faible. En effet, une auto corrélation des log rentabilités serait exploitée pour tirer des profits anormaux. Comme on le sait, le TCL (Théorème Central Limite) implique la normalité des rentabilités logarithmiques. Malgré les limites de ce modèle face à la réalité empirique (nous avons en effet constaté la forte lepto-kurticité des log-rentabilités des cours dans nos premiers résultats), c'est celui que nous adoptons et choisissons de représenter pour notre Bootstrap. Il a également l'avantage d'être cohérent avec les moyennes mobiles simples utilisées dans nos tests de performances. En effet, si les moyennes mobiles avaient été pondérées en accordant davantage d'importance aux dernières volatilités des cours, par des oscillateurs pondérés ou MACD, il aurait été cohérent d'utiliser un modèle autorégressif intégrant en plus l'hétéroscédasticité des cours, comme le ARCH.

La représentation que nous avons choisie des log-rentabilités est donc faite à l'aide d'un mouvement brownien géométrique, ainsi caractérisé en temps discret :

lnS(t+At) - lnS(t) ? AlnS=mAt+oAW avec W, un processus de Wiener, et oAW distribué selon une N(0, o²At)

Nous choisissons d'adopter un pas de 1 entre les points de la trajectoire, ce qui a pour but de réduire la complexité algorithmique, car la variable t disparaît.

En passant à l'exponentielle, on obtient :

_eAlnS = _emAt ? oAW_{? e}lnS(k ? 1) - lnS(k) ? _em + oW

accroissements par unité de temps.

Ayant calculé nos paramètres sur l'échantillon que constituent les cours du CAC40 sur une période de près de 10ans, nous avons obtenu ces valeurs :

Paramètres Stochastiques

m=E(AlnS(k)) o²=var(AlnS(k)) o drift 4u

-0.000247991 0.000253348 0.01591692 -0.00012132

Puis nous avons implémenté l'algorithme suivant, dont le code VBA Excel figure en annexe, pour un nombre n de points de la trajectoire Brownienne géométrique souhaitée :

Fonction W

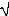
W = - 2 x Log(Random) x cos (27cx Random)

Fin

Fonction MBG

m + ox W

MBG = S0 x e

Fin

Procédure

Pour i de 1 à n

Faire

MBG

Boucler k fois `pour permettre converger en loi enregistrer MBG

Fin Pour

Fin

Dans notre modèle algorithmique, nous avons choisi, plutôt que d'utiliser le générateur de v.a.r gaussiennes centrées réduites d'Excel, de concevoir personnellement un tel générateur suivant la méthode de Box-Muller, pour ses propriétés de convergence rapide. Il faudrait réaliser plusieurs centaines, voir un millier d'itération pour obtenir des résultats significatifs pour une loi gaussienne. Par cette méthode, dans la pratique et pour obtenir des résultats intéressants, une cinquantaine d'itérations suffisent. Aussi, pour chaque point d'une trajectoire brownienne affiché, une cinquantaine sont calculés.

Nous avons donc choisi pour notre bootstrap, de ne simuler qu'une centaine de trajectoires browniennes géométriques. Cent une, exactement. Mais ces 101 trajectoires affichées pour le calcul des significativités correspondent à un total de 50 x 101, ie 5 050 trajectoires calculées en chaque point, à l'issu des 101 itérations.

Voici 3 exemples de trajectoires obtenues avec notre modèle Brownien géométrique (2^e au 4e chart), comparé aux cours réels (1^er chart) :

CAC40 (raw)

8000 7000 6000 5000 4000 3000 2000 1000 0

CAC40 (SIMULATION MBG)

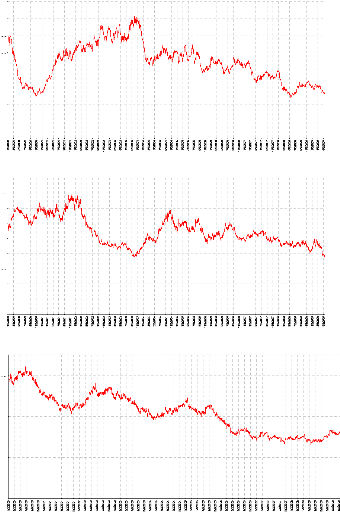
CAC40 (SIMULATION MBG)

CAC40 (SIMULATION MBG)

7000

6000

5000

4000

3000

2000

1000

0

8000

7000

6000

5000

4000

3000

2000

1000

0

9000

8000

7000

6000

5000

4000

3000

2000

1000

0