1.3 Modèles d'évaluation d'options
1.3.1 Modèle de Black & Scholes
La formule de Black & Scholes repose sur
l'hypothèse que les rendements de l'actif sous- jacent sont gaussiens,
ou de manière équivalente que la valeur de l'actif suit une
diffusion brownienne géométrique qui est solution de
l'équation différentielle stochastique suivante :
dSt = rStdt+o-StdWt
La formule proposée par Black et Scholes permet
d'évaluer le prix d'une option Call ou Put à partir des cinq
données suivantes:
- S0 la valeur actuelle de l'actif sous-jacent;
- T _ t le temps qui reste à l'option avant
échéance (en années);
- K le prix d'exercice fixé de l'option;
- r le taux d'intérêt sans risque;
- o- la volatilité du prix de l'action.
Ainsi, le prix théorique d'une option Call est
donné par:
C(S0, K, r, T, o-) = S0N(d1) _ Ke_r(T_t)N(d2).
De même, le prix théorique d'une option Put
s'écrit :
P(S0, K, r, T, o-) = _S0N(_d1) + Ke_r(T_t)N(_d2),
avec:
- N la fonction de répartition de la loi normale
centrée réduite N(0, 1);
[ln (S0 ) + (r + 1 2cr2) (T -
t)] ;
- d1 = 1
avT --t
- d2 = d1- a/T - t.
K
A partir de ce modèle, Merton (1973) propose une
généralisation de ces formules pour évaluer une option
à barrière Call de type Down & Out.
1.3.2 Les arbres trinomiaux
Le modèle trinomial de Ritchken
L'évaluation des options à barrière par
une méthode arborescente nécessite, pour des raisons de vitesse
de convergence, d'adapter la construction de l'arbre des prix de l'actif en
fonction du niveau de la barrière. En fait, il suffit de positionner un
niveau de prix de l'arbre exactement sur la valeur de la barrière pour
que la distribution mathématique du prix de l'option soit
respectée. En conséquence, l'emploi d'un arbre binomial est
inadapté au problème étudié. Le degré de
liberté supplémentaire dû à l'utilisation d'un arbre
trinomial permet d'ajuster très facilement l'arbre de sorte à
faire coïncider l'un des niveaux de prix du treillis avec la
barrière.
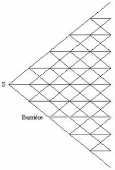
FIG. 1.3: Modèle trinomial de Ritchken pour
l'évaluation des options à barrière
Les niveaux du prix de l'actif au sein de l'arbre sont
donnés par:
S0ek~~(T_t),
avec:
- À une valeur adaptée de telle sorte que le
système de probabilités obtenu reste cohérent quelle que
soit la période considérée;
- o- la volatilité du prix de l'actif sous-jacent;
~~ et Ent
- k un entier relatif compris entre --Ent ~~N ~~N ~~ :
2 2
Afin que l'un des niveaux de prix correspondent au niveau B de
la barrière, il faut et il suffit
~~N ~~ et Ent ~~N ~~ tel que :
qu'il existe un entier relatif k, non nul et compris entre --Ent
2 2
~ B )
B = S0ek~~(T _t) ou encore k = 1
Àa(T -- t) ln S0
Selon Ritchken, il n'existe qu'une seule et unique valeur
À qui vérifie les équations précédentes. La
limite du modèle de Ritchken apparaît lorsque le niveau de la
barrière est proche du prix initial de l'actif. Dans ce cas, en dessous
d'un certain nombre de pas, il n'existe pas forcément d'entier k
strictement positif en valeur absolue permettant d'ajuster le paramètre
À.
Le modèle de Cheuk et Vorst
Pour une période donnée, plutôt que de
modifier les points les plus proches de la barrière, Cheuk et Vorst
(1996) multiplient toutes les valeurs possibles du prix de l'action par un
terme multiplicatif de telle sorte que l'un des niveaux du treillis des prix de
l'action coïncide avec la valeur de la barrière en cette date. La
figure ci-dessous illustre le type d'arbre trinomial qu'ils obtiennent :
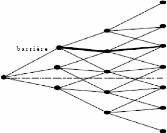
FIG. 1.4: Modèle trinomial de Cheuk et Vorst pour
l'évaluation des options à barrière
Cette méthode s'avère plus robuste que celle de
Ritchken de point de vue vitesse de convergence mais n'a pas pu relever les
limites qu'il a présentées (niveau de barrière très
proche du prix initial de l'actif).
| 


