Extraction des bases génériques informatives de règles sans calcul de fermetures

précédent sommaire suivant

4.5 Comparaisons des coilts des &tapes de PRINCE

Dans cette section, nous allons comparer les temps d'exécution des étapes constituant l'algorithme PRINCE. Rappelons que l'algorithme PRINCE est constitué de trois étapes, a savoir :

1. Détermination des générateurs minimaux (cf. la procédure GEN-GMS page 43) ;

2. Construction du treillis des générateurs minimaux (cf. la procedure GEN-ORDRE page 50) ;

3. Extraction des bases generiques informatives de regles (cf. la procedure GEN-BGRS page 53).

4.5.1 Bases benchmark

Dans toutes les figures qui vont suivre, et pour l'algorithme PRINCE, nous utilisons une valeur de minconf egale a 0 (cad que nous avons considere, pour une valeur de minsup fixee, le pire des cas par rapport au nombre de regles generees). Les comparaisons des etapes constituant PRINCE seront divisees en deux parties :

G Comparaisons sur des bases denses ;

G Comparaisons sur des bases eparses.

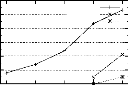
4.5.1.1 Comparaisons sur les bases denses

Les temps d'execution des differentes etapes de l'algorithme PRINCE sur les bases denses sont presentes par la figure 4.8 et le tableau 4.4.

- PUMSB et CONNECT : ces deux bases sont caracterisees par un nombre ainsi qu'une taille moyenne des transactions relativement eleves. Ces caracteristiques influent enormement sur la repartition du temps d'execution total de l'algorithme PRINCE par rapport aux trois etapes le constituant. Ainsi, la premiere etape, cad la determination des generateurs minimaux, est l'etape la plus coUteuse pour ces deux bases. 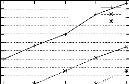La deuxieme et troisieme etape n'ont pas une influence significative sur les temps d'execution de PRINCE. En effet, pour la base PUMSB (resp. CONNECT), les temps d'execution de ces deux etapes ne depassent pas 1,28% (resp. 3,01%) du temps d'execution total de l'algorithme PRINCE.

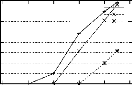
- CHESS : cette base est caracterisee par un nombre reduit de transactions. Cependant, la taille moyenne des transactions est elevee, ce qui influe sur les temps d'execution de la premiere etape. D'autant plus, CHESS permet d'extraire un nombre eleve de generateurs minimaux frequents atteignant 719 886 pour minsup 45%. Ce nombre maintient la premiere etape comme etant la plus cofiteuse. Le temps d'execution relatif a la construction du treillis des générateurs minimaux est lui aussi influence par le nombre de generateurs minimaux frequents extraits lors de la premiere etape. La troisieme etape, cad l'extraction des bases generiques de regles, est la moins cofiteuse. En effet, le temps d'execution de cette etape ne depasse pas 2,06% du temps d'execution total de l'algorithme PRINCE.

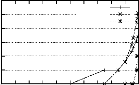
- MUSHROOM : cette base est caracterisee par un nombre reduit de transactions ainsi qu'une taille moyenne reduite des transactions. Ainsi, la premiere etape ne pese pas lourd sur les performances de l'algorithme PRINCE. Cependant, le nombre de generateurs minimaux frequents, atteignant 360 166 pour minsup:0,1, extraits lors de cette premiere etape influe sur le temps d'execution de la deuxieme etape. Ainsi, cette derniere est la plus coUteuse. Il faut noter que comme pour les trois premieres bases, la troisieme etape n'a pas une influence significative sur les temps d'execution de l'algorithme PRINCE. Son temps d'execution ne depasse pas 10% du temps d'execution total.

Ces comparaisons confirment que, etant le treillis des générateurs minimaux construit, l'extraction des bases generiques de regles devient immediate et n'a pas d'influence notable sur les performances de l'algorithme PRINCE.

Temps d'execution (en seconde)

4096

1024

256

64

16

4

1

95

90

Pumsb

85

étape 1
étape 2
étape 3

80

75

Temps d'execution (en seconde)

1024

256

512

128

64

32

16

4

2

8

1

90

80

Connect

70

étape 1
étape 2
étape 3

60

50

Minsup (en %)

Temps d'execution (en seconde)

256

128

64

32

16

4

2

8

1

90

80

70

Chess

60

étape 1
étape 2
étape 3

50

40

Minsup (en %) Minsup (en %)

Temps d'execution (en seconde)

64

32

16

4

2

8

1

20

18

16

14

Mushroom

12

10

étape 1
étape 2
étape 3

8

6

4

2

0

Minsup (en %)

FIG . 4.8 -- Temps d'execution des etapes constituant PRINCE pour les bases denses

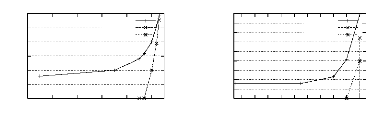
4.5.2.1 Comparaisons sur les bases eparses

Les temps d'execution des differentes etapes de l'algorithme PRINCE sur les bases eparses sont presentes par la figure 4.9 et le tableau 4.5.

transactions reduite (10 items). Pour des valeurs de minsup superieures ou egales a 0,5%, chaque generateur minimal frequent est aussi un ferme. L'algorithme PRINCE n'execute donc pas sa deuxieme etape. Cependant, ce n'est plus le cas pour des supports inferieurs A 0,5%. Le temps d'execution de la deuxieme etape croit alors proportionnellement au nombre de generateurs minimaux extraits lors de la premiere etape. Il est important de noter que la construction de l'ordre partiel est influence par l'augmentation de la taille de la bordure negative des generateurs minimaux GBd^-. En effet, dans le cas des bases eparses, le treillis des itemsets frequents tend a se confondre avec le treillis des generateurs minimaux. Ainsi, la quasi-totalite des itemsets sont des generateurs minimaux. Grace a la metrique statistique minsup, ces itemsets sont consideres generalement comme infrequents. Cette augmentation dans la taille de la bordure negative GBd^- induit une augmentation dans l'espace de recherche des supports adequats lors de la construction de l'ordre partiel. La troisieme etape presente un temps d'execution negligeable etant donne que le nombre de generateurs minimaux frequents extraits reste reduit meme pour des valeurs tres basses de minsup. Pour minsup=0,02, le nombre de generateurs minimaux frequents est egal a 109 940.

- T4 O!1 OD1 OOK : cette base est caracterisee par un nombre eleve de transactions ainsi qu'une taille moyenne des transactions elevee (40 items). Ainsi, la premiere etape s'avere la plus cofiteuse. Pour des valeurs de minsup superieures ou egales a 1,5%, chaque generateur minimal frequent est aussi un ferme et la deuxieme etape n'est pas executee. Pour des valeurs de minsup inferieures a 1,5%, chaque generateur minimal frequent n'est plus un ferme. De plus, le nombre de candidats generateurs minimaux augmente considerablement en passant de minsup=1,5% a minsup=0,5%. En effet, pour minsup=1,5%, le nombre de candidats generateurs minimaux est egal a 276 886 alors qu'il est egal a 3 452 429 pour minsup=0,5%. Ceci explique le saut dans les temps d'execution de PRINCE entre ces deux valeurs de minsup. La troisieme etape reste la moins cofiteuse. Son cofit ne depasse pas 2,74% du temps d'execution total.

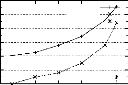
- RETAIL : comme c'est le cas pour la base T10I4D100K, la base RETAIL est caracterisee par un nombre eleve de transactions et par une taille moyenne reduite des transactions. La premiere etape est la plus coUteuse comparee a la deuxieme et a la troisieme etape. La deuxieme etape est penalisee par l'augmentation de la taille de la bordure negative des generateurs minimaux GBd^-. En effet, RETAIL est caracterisee par un nombre eleve d'items et dont la quasi-totalite sont qualifies de frequents avec les valeurs de minsup utilisees dans nos tests (pour minsup=0,01%, 9 300 1-itemsets, parmi 16 470, sont frequents).

Ce nombre d'items fréquents entraine la génération d'un nombre élevé de candidats et dont la plupart sont infréquents. Ceci explique l'augmentation du temps d'exécution de la deuxième étape en passant de minsup=0,02% a minsup=0,01%. La troisième étape reste la moins cofiteuse et son temps d'exécution est négligeable comparativement aux deux premières étapes.

Il est intéressant de noter que pour une même valeur de minsup égale a 0,5%, le temps d'exécution ainsi que le nombre de générateurs minimaux fréquents extraits des bases T10I4D100K et RETAIL sont comparables. En effet, le temps d'exécution total est presque égal au temps d'exécution de la première étape. De plus, le nombre de générateurs minimaux fréquents extraits de T10I4D100K (resp. RETAIL) est égal a 1 074 (resp. 582) pour une taille maximale d'un générateur minimal fréquent égal a 6 (resp. 5) items. Ces résultats peuvent être expliqués par un nombre de transactions relativement proche pour ces deux bases, ainsi qu'une même taille moyenne des transactions. Cependant, en comparant les résultats de ces deux bases a ceux de la base T40I10D100K pour la même valeur de minsup (cad 0,5%), nous (cad 0,5%), nous notons une différence significative. En effet, le nombre de générateurs minimaux fréquents extraits de la base T40I10D100K pour cette valeur de minsup est égal a 1 276 055. Ceci représente presque 1 188 (resp. 2 193) fois le nombre de générateurs minimaux fréquents généré dans T10I4D100K (resp. RETAIL). De même la taille maximale d'un générateur minimal fréquent atteint 18 items. Ainsi, bien que les trois bases T10I4D100K, T40I10D100K et RETAIL ont pratiquement le même nombre de transactions, leurs tailles moyenne des transactions expliquent la différence dans le nombre de générateurs minimaux extraits. En effet, la taille moyenne des transactions dans le cas de T40I10D100K, égale a 40 items, est quatre fois plus élevée que celles des deux autres bases, égales a 10 items.

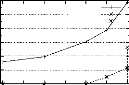
- ACCIDENTS : cette base est caractérisée par un nombre très élevé de transactions avec une taille moyenne importante. Ces caractéristiques ont pour conséquence le fait que le temps d'exécution de la première étape domine le temps d'exécution total de l'algorithme PRINCE. Il faut noter que pour des valeurs de minsup supérieures ou égales a 40%, chaque générateur minimal fréquent est aussi un fermé et PRINCE n'a pas a exécuter sa deuxième étape. Comme pour toutes les bases benchmark testées, la troisième étape, cad l'extraction des bases génériques informatives de règles, est la moins conteuse parmi les trois étapes constituant l'algorithme PRINCE.

TAB . 4.5 -- Tableau comparatif des étapes constituant PRINCE pour les bases éparses.

0.55

0.45

0.35

0.25

Minsup (en %)

T40I10D100K

512

étape 1
étape 2
étape 3

64

32

16

8

4

2

1

0.15 0.05 9.5 8.5 7.5 6.5 5.5 4.5 3.5 2.5 1.5 0.5

Minsup (en %)

Temps d'execution (en seconde)

Temps d'execution (en seconde)

T10I4D100K

étape 1
étape 2
étape 3

64

32

16

8

4

2

1

256

128

Temps d'execution (en seconde)

4096

1024

256

64

16

4

1

0.1

0.08

0.06

Retail

étape 1
étape 2
étape 3

0.04

0.02

0

Minsup (en %)

Temps d'execution (en seconde)

4096

1024

256

64

16

4

1

90

80

70

Accidents

60

étape 1
étape 2
étape 3

50

40

30

Minsup (en %)

FIG . 4.9 -- Temps d'exécution des étapes constituant PRINCE pour les bases éparses

4.5.2 Bases "pire des cas"

Lors de ces expérimentations, nous avons utilisé une valeur de minconf égale a 0. Pour toutes ces expérimentation, la valeur de minsup est fixée a 1. Nous avons testé 26 bases "pire des cas" représentant la variation de la valeur de n de 1 a 26.

Etant donné que ces bases représentent le pire des cas, tout itemset candidat est un générateur minimal fréquent et est égal a sa fermeture. Ainsi, l'algorithme PRINCE n'exécute pas sa deuxième étape, cad celle relative a la construction du treillis des générateurs minimaux. La première étape est la plus cofiteuse étant donné le nombre, égal a 2', de candidats générés a partir de chaque base "pire des cas". La troisième étape est moins cofiteuse que la première étape. Cependant, a partir d'une valeur de n supérieure ou égale A 24, les temps d'exécution de cette étape commencent a prendre de l'importance. Ceci peut être expliqué par le fait que les accès, aux informations nécessaires a l'exécution de cette étape, s'exécutent dans l'espace d'échange et non plus en mémoire centrale. Ainsi, ces accès deviennent de moins en moins rapides. En effet, l'exécution des bases "pire des cas" est exigeante en espace mémoire et sature rapidement la mémoire centrale bien que nous minimisons la redondance en utilisant un seul trie au lieu de plusieurs. 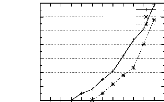Ceci explique l'arrêt de l'exécution de l'algorithme pour n=26. Les temps d'exécution des différentes

Temps d'execution (en seconde)

16384

4096

1024

256

64

16

4

1

étape 1
étape 2
étape 3

15 16 17 18 19 20 21 22 23 24 25

n

FIG . 4.10 -- Temps d'exécution des étapes constituant PRINCE pour les bases "pire des cas"

étapes de l'algorithme PRINCE sur les bases "pire des cas" sont présentés par la figure 4.10 et le tableau 4.6. Dans ce dernier, "/" signifie que l'exécution n'a pas pu arriver a terme.

4.6 Performances de PRINCE vs. CLOSE, A-CLOSE et TITANIC

Dans cette section, nous allons comparer les performances de notre algorithme PRINCE a respectivement celles des algorithmes CLOSE, A-CLOSE et TITANIC.

4.6.1 Bases benchmark

Les expérimentations seront divisées en deux parties : G Expérimentations sur des bases denses ;

Expérimentations sur des bases éparses.

4.6.1.1 Experimentations sur les bases denses

Les temps d'exécution de l'algorithme PRINCE comparés respectivement aux algorithmes CLOSE, A-CLOSE et TITANIC sur les bases denses sont présentés par la figure 4.11 et le tableau 4.7. Dans ce dernier, les trois dernières colonnes indiquent le facteur multiplicatif des temps d'exécution de CLOSE, A-CLOSE et TITANIC par rapport a l'algorithme PRINCE. "/" signifie que l'exécution n'a pas pu arriver a terme et que le ratio correspondant ne peut être calculé.

TAB . 4.6 -- Tableau comparatif des étapes constituant PRINCE pour les bases ¹¹pire des cas¹¹.

- PUMSB : pour cette base, les performances de PRINCE sont meilleures que celles de CLOSE, A-CLOSE et TITANIC pour toutes les valeurs de minsup. Les performances de CLOSE et A-CLOSE se dégradent considérablement étant donné qu'ils effectuent des intersections sur un grand nombre de transactions de taille élevée. Le mécanisme de comptage par inférence adopté par TITANIC s'avère plus efficace que le calcul des intersections adopté par CLOSE et A-CLOSE. Ceci peut être expliqué par le nombre réduit d'items fréquents a prendre en considération lors du calcul de la fermeture d'un générateur minimal fréquent. En effet, pour minsup = 75%, seulement 27 items parmi 7 117 possibles sont fréquents et la taille maximale d'un générateur minimal fréquent est égale a 12 items. Les performances de PRINCE peuvent être expliquées par le fait que les traitements = effectuer pour un générateur minimal fréquent sont beaucoup moins coUteux que ceux effectués pour les trois autres algorithmes. D'autant plus, les fonctions de gestion des classes d'équivalence permettent a PRINCE d'éviter un calcul redondant des fermetures tel que c'est le cas pour A-CLOSE, CLOSE et TITANIC. En effet, pour une valeur de minsup égale a 75%, le nombre de générateurs minimaux fréquents (égal a 248406) est presque égal = 2,46 fois le nombre d'itemsets fermés fréquents (égal a 101 083).

la base PUMSB, est caracterisee par un grand nombre de transactions de taille elevee. Ces caracteristiques compliquent la tache de CLOSE et A-CLOSE qui effectuent des operations coUteuses d'intersection. PRINCE et TITANIC evitent ces calculs coUteux avec un avantage pour PRINCE. En effet, PRINCE est avantage par un coUt reduit des comparaisons effectuees pour un generateur minimal frequent compare aux tentatives d'extension executees pour un generateur minimal frequent dans le cas de TITANIC. Il est a noter que pour une valeur de minsup = 50%, l'execution de TITANIC n'a pu se terminer pour manque d'espace memoire. Dans cette base, et malgre qu'il n'y a aucun calcul redondant des fermetures pour les trois algorithmes CLOSE, A-CLOSE et TITANIC (le nombre de generateurs minimaux frequents est egal a celui des itemsets fermes frequents), les performances de notre algorithme restent les meilleures.

Vu le nombre de transactions et la taille moyenne des transactions qui caracterisent les bases PUMSB et CONNECT, le calcul des supports des candidats constituent une operation coUteuse pour les algorithmes testes. Ainsi, la representation compacte de la base adoptee dans PRINCE et l'utilisation d'un fichier binaire dans le cas des trois autres algorithmes constituent des tentatives de reduction du coUt de cette operation.

- - CHESS : pour cette base, les performances de PRINCE sont largement meilleures que celles de CLOSE, A-CLOSE et TITANIC pour toutes les valeurs de minsup. Comme pour les deux premieres bases, notre algorithme est avantage par un coUt reduit des traitements a executer pour chaque generateur minimal frequent compare aux trois autres algorithmes. Le mecanisme de comptage par inference adopte par TITANIC s'avere plus efficace que le calcul des intersections adopte par les algorithmes CLOSE et A-CLOSE. Cependant, cette efficacite tend a diminuer avec la baisse de la valeur de minsup. En effet, pour calculer les itemsets fermes frequents, TITANIC essaie d'etendre tout generateur minimal frequent par les items frequents adequats. Ceci necessite des recherches de supports dont le nombre augmente avec l'augmentation du nombre d'items frequents, chaque fois que la valeur de minsup diminue.

- MUSHROOM : dans le cas de la base MUSHROOM, PRINCE est encore une fois meilleur que CLOSE, A-CLOSE et TITANIC. Pour cette base, l'etape de calcul du support ne pese pas lourd sur les performances des quatre algorithmes (vu le nombre reduit de transactions dans la base MUSHROOM ainsi que la taille moyenne reduite des transactions). Cependant, les operations relatives a la construction de l'ordre partiel dans le cas de PRINCE et au calcul des fermetures dans le cas des trois autres algorithmes sont les operations

les plus coUteuses. Les performances de notre algorithme restent meilleures etant donne l'importance du role joue par les fonctions de gestion des classes d'equivalence. En effet, pour une valeur de minsup egale a 0,1%, le nombre de generateurs minimaux frequents (egal a 360 166) est presque egal a 2,20 fois le nombre d'itemsets fermes frequents (egal a 164117). De meme, l'utilisation d'une liste prohibee au niveau de chaque classe d'equivalence permet de reduire considerablement le nombre de comparaisons et donc d'ameliorer les performances de notre algorithme. Ainsi, bien que CLOSE et A-CLOSE beneficient d'un nombre reduit de transactions ainsi qu'une taille moyenne des transactions relativement petite sur lesquelles ils executent des intersections, ces deux algorithmes sont handicapes par un calcul redondant des fermetures. De son cote, TITANIC fait mieux que CLOSE et A-CLOSE pour des supports compris entre 20% et 2% alors que la tendance est largement inversee en faveur de CLOSE et A-CLOSE pour des supports au dessous de 2%. Ceci peut etre explique par le fait que TITANIC effectue beaucoup de recherches des items adequats. Le nombre de ces recherches augmente considerablement, avec la baisse des valeurs de minsup, etant donne que le nombre d'items frequents devient eleve. En effet, pour minsup : 0,1%, 116 items sont frequents parmi 119 possibles et la taille maximale d'un generateur minimal frequent est egale a 10 items seulement.

L'algorithme PRINCE s'avere performant sur les bases denses et pour toutes les valeurs de minsup. La difference entre les performances de PRINCE et celles de CLOSE et A-CLOSE atteint son maximum pour la base PUMSB. En effet, PRINCE est environ 160 (resp. 403) fois plus rapide que CLOSE (resp. A-CLOSE) pour un support de 85%. De meme, PRINCE est environ 538 fois plus rapide que TITANIC pour la base MUSHROOM et pour un support egal a 0,01%. Pour ces bases denses, PRINCE est en moyenne 42 (resp. 89 et 41) fois plus rapide que CLOSE (resp. A-CLOSE et TITANIC).

4.6.1.2 Experimentations sur les bases eparses

Les temps d'execution de l'algorithme PRINCE compares respectivement aux algorithmes CLOSE, A-CLOSE et TITANIC sur les bases eparses sont presentes par la figure 4.12 et le tableau 4.8. Dans ce dernier, les trois dernieres colonnes indiquent le facteur multiplicatif des temps d'execution de CLOSE, A-CLOSE et TITANIC par rapport a l'algorithme PRINCE. "/" signifie que l'execution n'a pas pu arriver a terme et que le ratio correspondant ne peut etre calcule.

TAB . 4.7 - Tableau comparatif des resultats experimentaux de PRINCE vs. A-CLOSE, CLOSE et TITANIC pour les bases denses.

Temp d'execution (en seconde)

65536

16384

4096

1024

256

64

16

4

90

80

Connect

70

Prince

Close A-Close Titanic

60

50

Temps d'execution (en seconde)

262144

65536

16384

4096

1024

256

64

16

4

1

95

90

Pumsb

85

Prince

Close A-Close Titanic

80

75

65536

16384

4096

1024

256

64

16

4

1

Temps d'execution (en seconde)

m insup (en %)

16384

4096

1024

256

64

16

4

1

Temps d'execution (en seconde)

Chess

Prince

Close A-Close Titanic

90 80 70 60 50 40

m insup (en %)

m insup (en %)

Mushroom

Prince

Close A-Close Titanic

20 18 16 14 12 10 8 6 4 2 0

m insup (en %)

FIG . 4.11 -- Les performances de PRINCE vs. CLOSE, A-CLOSE et TITANIC pour les bases denses

PRINCE fait mieux que cet algorithme pour des valeurs de minsup supérieures ou égales a 0,03%. Alors que c'est l'inverse pour des supports inférieurs a 0,03%. Ceci peut être expliqué par le fait que PRINCE est pénalisé par le coiit de la construction de l'ordre pour de tres basses valeurs de minsup. Cependant, CLOSE est avantagé par une taille moyenne des transactions relativement faible (10 items). Notons que pour des valeurs de minsup supérieures ou égales a 0,5%, chaque générateur minimal fréquent est un fermé. Ainsi, PRINCE ne nécessite pas l'exécution de la procédure GEN-ORDRE étant donné que l'ordre est déjà construit a la fin de la premiere étape. De son coté, A-CLOSE n'effectue aucun calcul de fermeture. Ainsi, A-CLOSE prend le dessus sur CLOSE. Cependant, comparé a PRINCE pour les mêmes valeurs de support (supérieures ou égales a 0,5%), A-CLOSE se voit moins rapide en raison du balayage supplémentaire de l'ensemble des générateurs minimaux fréquents de taille (k-1) effectué pour chaque candidat g de taille k. Ce balayage permet de comparer le support de g a celui de ses sous-ensembles de taille (k-1) afin de savoir si g est minimal ou non. Au fur et a mesure que la valeur de minsup diminue, les performances de TITANIC se dégradent considérablement. En effet, le nombre d'items fréquents, a considérer dans le calcul de la fermeture d'un générateur minimal fréquent, croit énormément suite a la baisse des valeurs de minsup. Ainsi, pour minsup=0,02%, 859

items sont frequents parmi 1 000 possibles et la taille maximale d'un generateur minimal frequent est egale a 10 items seulement.

- T40I10D1OOK : les performances de PRINCE dans cette base sont largement meilleures que celles de CLOSE, A-CLOSE et TITANIC quelle que soit la valeur de minsup. Pour les valeurs de minsup superieures ou egales a 1,5%, le scenario de la base T10I4D100K, pour des valeurs de minsup superieures ou egales a 0,5%, semble se repeter. En effet, pour ces valeurs, chaque generateur minimal frequent est aussi un ferme. Pour des supports inferieurs a 1,5%, A-CLOSE est oblige de calculer les fermetures. Ainsi, CLOSE et A-CLOSE sont handicapes par une taille moyenne elevee des transactions (40 items) sachant que CLOSE prend le dessus sur A-CLOSE. De même, les performances de TITANIC se degradent d'une manière considerable pour les mêmes raisons evoquees auparavant. Le coUt des comparaisons, dans le cas de PRINCE, etant nettement plus reduit que le coUt du calcul des intersections (resp. des tentatives d'extension) pour calculer la fermeture d'un generateur minimal frequent dans le cas de CLOSE et A-CLOSE (resp. TITANIC) explique l'ecart dans les performances entre PRINCE et les trois autres algorithmes.

- - RETAIL : pour cette base, notre algorithme realise des temps d'execution beaucoup moins importants que ceux realises par CLOSE, A-CLOSE et TITANIC. Pour des valeurs de minsup superieures a 0,08%, les temps d'execution de PRINCE, CLOSE et A-CLOSE restent comparables avec un avantage pour PRINCE. Pour des valeurs de minsup superieures a 0,06%, les performances de PRINCE et A-CLOSE restent comparables avec un avantage pour PRINCE. Toutefois, les performances de CLOSE se degradent considerablement. Pour des valeurs de supports inferieures a 0,06%, les performances de A-CLOSE se degradent aussi d'une manière significative. Ces performances peuvent être expliquees par l'influence enorme du nombre eleve d'items dans RETAIL. En effet, CLOSE est handicape par un nombre enorme de candidats pour lesquels il est oblige de calculer la fermeture alors qu'un grand nombre d'entre eux s'avèrera non frequent. Le nombre de candidats affecte aussi les performances de A-CLOSE a cause des balayages supplementaires ainsi que le coUt du calcul des fermetures. De son cote, TITANIC est considerablement alourdi par un grand nombre d'items frequents a considerer lors du calcul de la fermeture d'un generateur minimal frequent (pour minsup = 0,04%, 4 463 items sont frequents et la taille maximale d'un generateur minimal frequent est egale a 6 items seulement). L'execution de TITANIC, pour des supports inferieurs a 0,04%, s'arrête pour manque d'espace memoire. PRINCE fait mieux que les trois autres algorithmes etant donne que les traitements relatifs a chaque generateur minimal sont nettement moins coUteux.

- ACCIDENTS : dans cette base, les performances de PRINCE sont meilleures que celles de CLOSE, A-CLOSE et TITANIC pour toutes les valeurs de minsup. Pour des valeurs de minsup superieures ou egales a 40%, chaque generateur minimal frequent est un ferme. Ainsi, le meme scenario, que dans les cas des bases T10I4D100K et T40D10I100K pour des supports respectivement superieurs ou egaux a 0,5% et 1,5%, s'est repete. CLOSE est enormement desavantage par un nombre eleve de transactions que contient ACCIDENTS ainsi qu'une taille moyenne des transactions relativement elevee. Ceci induit des coits enormes pour le calcul des fermetures. Pour des supports inferieurs a 40%, PRINCE doit executer sa deuxieme etape (cad la procedure GEN-ORDRE) pour construire l'ordre partiel. Les performances de A-CLOSE se degradent d'une maniere considerable etant donne qu'il est oblige de calculer les fermetures sur un nombre eleve de transactions. Le mecanisme de comptage par inference adopte par TITANIC s'avere plus efficace que le calcul des intersections adopte par CLOSE et A-CLOSE. Ceci peut etre explique par le nombre reduit d'items frequents a prendre en consideration lors du calcul de la fermeture d'un generateur minimal frequent. En effet, seuls 32 items parmi 468 sont frequents pour minsup egal a 30% et la taille maximale d'un generateur minimal frequent est egale a 12 items. Pour la base ACCIDENTS et pour toutes les valeurs de minsup, l'operation consistant en le calcul des supports des candidats pese enormement lourd sur les quatre algorithmes (il y a un nombre eleve de transactions de taille moyenne relativement elevee). Ainsi, dans le cas de l'algorithme PRINCE, la representation compacte de la base presente une solution importante pour faire face au coit de cette operation. Il en est de meme pour la raison de l'utilisation d'un fichier binaire en entree des trois autres algorithmes.

L'algorithme PRINCE s'avere aussi performant sur les bases eparses et pour toutes les valeurs de minsup. La difference entre les performances de PRINCE et celles de CLOSE et TITANIC atteint son maximum pour la base RETAIL. En effet, PRINCE est environ 115 (resp. 261) fois plus rapide que CLOSE (resp. TITANIC) pour un support de 0,04%. De meme, PRINCE est environ 57 fois plus rapide que A-CLOSE pour la base ACCIDENTS et pour une valeur de minsup egale a 30%. Pour ces bases eparses, PRINCE est en moyenne 31 (resp. 13 et 32) fois plus rapide que CLOSE (resp. A-CLOSE et TITANIC).